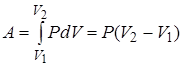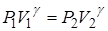Работа, совершаемая газом при изопроцессах
Изобарный 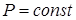 .
.
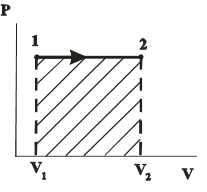 | Диаграмма этого процесса (изобары) в координатах 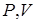 изображается прямой, параллельной оси изображается прямой, параллельной оси 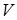 (рис. 14.2). При изобарном процессе работа газа при расширении объёма от (рис. 14.2). При изобарном процессе работа газа при расширении объёма от 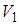 до до 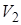 равна: равна:
| |
| Рис. 14.2 |
И определяется площадью заштрихованного прямоугольника на рис. 14.2.
Изохорный процесс ( 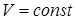 ). Диаграмма этого процесса
). Диаграмма этого процесса
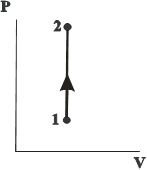 | (изохора) в координатах 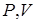 изображается прямой, параллельной оси ординат (рис. 14.3). поскольку изображается прямой, параллельной оси ординат (рис. 14.3). поскольку 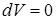 , то , то 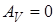 . Изотермический процесс ( . Изотермический процесс ( 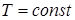 ). (рис. 14.4). Воспользовавшись уравнением состояния идеального газа Менделеева- Клайперона для работы в изотермическом процессе получаем: ). (рис. 14.4). Воспользовавшись уравнением состояния идеального газа Менделеева- Клайперона для работы в изотермическом процессе получаем: | ||
| Рис. 14.3 | |||
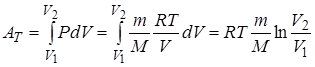 | |||
Изотермический процесс является идеальным процессом, т.к. расширение газа при постоянной температуре может происходить только бесконечно медленно. При конечной скорости расширения возникнут градиенты температуры.
12. Адиабатический (адиабатный) процесс
Это процесс, происходящий без теплообмена с окружающими телами. Рассмотрим, при каких условиях можно реально осуществить адиабатический процесс, или приблизиться к нему.
1. Необходима адиабатическая оболочка, теплопроводность которой равна нулю. Приближением к такой оболочке может служить сосуд Дьюара.
2. 2-ой случай – процессы, протекающие очень быстро. Теплота не успевает распространиться и в течение некоторого времени можно полагать 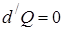 .
.
3. Процессы, протекающие в очень больших объёмах газа, например, в атмосфере (области циклонов, антициклонов). Для выравнивания температуры передача теплоты должна происходить из соседних, более нагретых слоёв воздуха, на это часто требуется значительное время.
Для адиабатического процесса первый закон термодинамики:
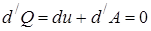
или 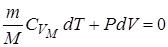 .
.
В случае расширения газа 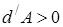 ,
, 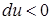 , (температура понизится). Если произошло сжатие газа
, (температура понизится). Если произошло сжатие газа 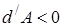 , то
, то 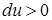 (температура повышается). Выведем уравнение, связывающее параметры газа при адиабатическом процессе. Учтём, что для идеального газа
(температура повышается). Выведем уравнение, связывающее параметры газа при адиабатическом процессе. Учтём, что для идеального газа 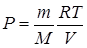 , тогда
, тогда
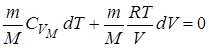
Разделим обе части уравнения на 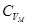 :
:
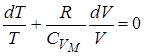 .
.
Из уравнения Майера 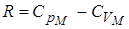 , тогда
, тогда
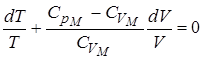 .
.
Обозначим 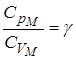 .
.
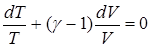 .
.
Проинтегрируем это уравнение:
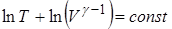 |
Отсюда
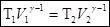
Получили уравнение Пуассона (для адиабаты) (1 – ая форма). Заменим 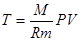 :
:
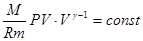 ,
,
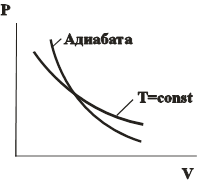 | т.к. для данной массы газа 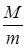 величина постоянная, то величина постоянная, то 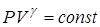
2 – ая форма уравнения Пуассона. На рис. 14.5 представлены сравнительные графики изотермы и адиабаты. | |
| Рис. 14.5 |
Так как 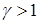 , то график адиабаты более крутой по сравнению с изотермой. Вычислим работу при адиабатическом процессе:
, то график адиабаты более крутой по сравнению с изотермой. Вычислим работу при адиабатическом процессе:
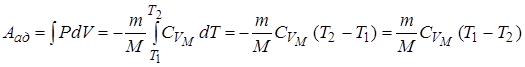
т.е 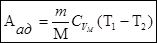
13.
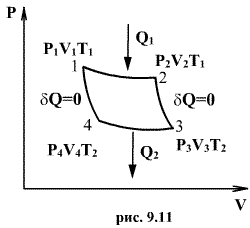
Анализируя работу тепловых двигателей, французский инженер С. Карно в 1824г. пришел к выводу, что наивыгоднейшим круговым процессом является обратимый круговой процесс, состоящий из двух изотермических и двух адиабатических процессов, т.к. он характеризуется наибольшим коэффициентом полезного действия. Такой цикл получил название цикла Карно. В прямом цикле Карно рабочее тело изотермически, а затем адиабатически расширяется, после чего снова изотермически (при более низкой температуре) и потом адиабатически сжимается. Т.е. цикл Карно ограничен двумя изотермами и двумя адиабатами.
При изотермическом расширении от нагревателя отбирается тепло 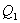 (на участке 1-2 рис. 9.11). Вследствие этого температура газа поддерживается неизменной. Соответственно, параметры точки 2 будут равны
(на участке 1-2 рис. 9.11). Вследствие этого температура газа поддерживается неизменной. Соответственно, параметры точки 2 будут равны 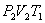 . На участке 2-3 происходит адиабатное расширение. Внутренняя энергия газа уменьшается и его температура падает до Т2. Параметры точки 3 -
. На участке 2-3 происходит адиабатное расширение. Внутренняя энергия газа уменьшается и его температура падает до Т2. Параметры точки 3 - 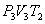 . На участке 3-4 газ изотермически сжимается. Параметры точки 4 -
. На участке 3-4 газ изотермически сжимается. Параметры точки 4 - 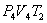 . Выделяющееся при этом тепло
. Выделяющееся при этом тепло 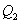 отбирается холодильником. Участок 4-1 -адиабатическое сжатие до исходного состояния, соответствующего точке 1. Таким образом, завершен цикл “1-2-3-4-1 и в итоге нагреватель отдал газу теплоту
отбирается холодильником. Участок 4-1 -адиабатическое сжатие до исходного состояния, соответствующего точке 1. Таким образом, завершен цикл “1-2-3-4-1 и в итоге нагреватель отдал газу теплоту 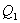 , а холодильник отобрал
, а холодильник отобрал 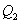 Разность
Разность 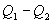 определяет полезную работу газа за один цикл, так как согласно I началу термодинамики
определяет полезную работу газа за один цикл, так как согласно I началу термодинамики 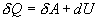 , но для кругового процесса
, но для кругового процесса 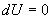 и, следовательно
и, следовательно 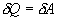 .
.
Отношение полезной работы к затраченной энергии нагревателя определяет коэффициент полезного действия (к.п.д.) тепловой машины:
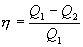 | (9.23) |
Эта формула справедлива для любого обратимого и необратимого процесса.
Определим коэффициент полезного действия цикла Карно для обратимого процесса. Теплота подводится на участке 1-2 и отводится на участке 3-4. Для изотермического процесса внутренняя энергия Q=const и все подводимое тепло расходуется на работу 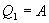 .
.
Тогда
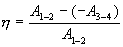
или
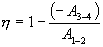
Для изотермического процесса работа
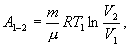
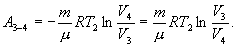
С учетом последних выражений
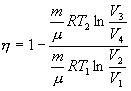 | (9.24) |
Покажем, что
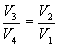
Так как процессы на участках 2-3 и 1-4 адиабатические, для определения связи между 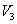 и
и 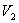 и
и 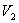 и
и 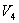 используем уравнение Пуассона в виде
используем уравнение Пуассона в виде 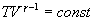
Следовательно,
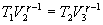
и
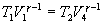
Разделим эти уравнения и получим
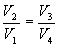
Тогда выражение для к.п.д. (9.24) примет вид
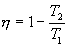
Эта формула справедлива только для обратимого цикла Карно.
Теоремы Карно.
- Все обратимые машины, работающие по циклу Карно, имеют, независимо от природы рабочего тела, одинаковый КПД при условии если у них общий нагреватель и холодильник.
- Если две тепловые машины имеют общий нагреватель и холодильник и одна обратимая, а другая необратимая, то КПД обратимой больше необратимой
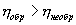
Электричество.
1. . Понятие электростатического поля.
Все тела в природе способны электризоваться, т.е. приобретать заряд. Наличие электрического заряда проявляется в том, что заряженные тела взаимодействуют друг с другом. Существует два типа электрических зарядов, условно названных отрицательными и положительными. Носителями отрицательного заряда являются в основном электроны; ядра атомов заряжены положительно. Полагают, что существование этих двух типов заряда является проявлением симметрии природы (как, например, левое и правое). Другим фундаментальным свойством заряда является его дискретность, его кратность, хоть и малой, но вполне определенной величине. В электрически изолированной системе общий заряд системы не изменяется (закон сохранения заряда). Поле, создаваемое электрическими зарядами и обнаруживающее себя воздействием на другие заряды называется электрическим полем. Если заряды неподвижны и поле не изменяется, то поле называется электростатическим.
Взаимодействие зарядов описывается законом Кулона. Если расстояние между заряженными телами много больше размеров тел, заряды можно считать точечными.
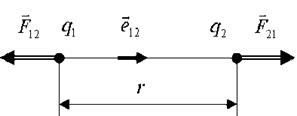
Закон Кулона. Сила взаимодействия точечных неподвижных зарядов в вакууме прямо пропорциональна величине зарядов и обратно пропорциональна квадрату расстояния между ними. Для одноименных зарядов (рис. 16.1)
 | 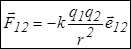 где где 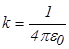 - коэффициент пропорциональности, - коэффициент пропорциональности, 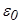 - электрическая постоянная ( - электрическая постоянная ( 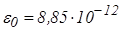 Ф/м); Ф/м); |
| Рис. 16.1 |
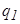 ,
, 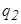 - величины электрических зарядов;
- величины электрических зарядов; 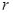 – расстояние между зарядами;
– расстояние между зарядами; 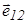 – единичный вектор;
– единичный вектор; 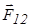 – сила, действующая на заряд
– сила, действующая на заряд 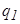 со стороны заряда
со стороны заряда 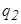 . Знак «-» обусловлен тем, что сила
. Знак «-» обусловлен тем, что сила 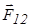 направлена противоположно вектору
направлена противоположно вектору 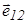 .
.
Пример использования закона Кулона.
Задача. Найти силу взаимодействия заряженного стержня с зарядом 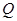 и длиной и длиной 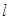 с точечным зарядом с точечным зарядом 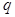 , находящимся на расстоянии , находящимся на расстоянии 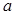 от края стержня на одной прямой с ним. Дано: от края стержня на одной прямой с ним. Дано: 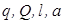 . Найти: . Найти: 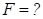 | 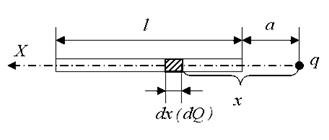 |
| Рис. 16.2 |
Решение. Разобьем стержень (рис. 16.2) на дифференциально малые элементы длиной 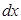 с зарядом
с зарядом 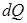 , которые мы можем считать точечными. Сила взаимодействия заряда
, которые мы можем считать точечными. Сила взаимодействия заряда 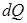 с
с 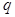 по закону Кулона
по закону Кулона 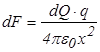 . Представим
. Представим 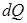 как заряд, приходящийся на единицу длины
как заряд, приходящийся на единицу длины 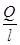 , умноженный на длину элемента
, умноженный на длину элемента 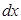 , т.е.
, т.е. 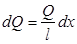 , тогда
, тогда 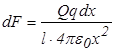 . Интегрируя по длине стержня, получим
. Интегрируя по длине стержня, получим 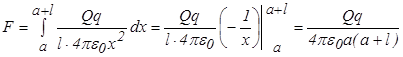 .
.
Заметим, что при 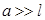
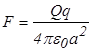 , т.е. стержень уже можно считать точечным зарядом.
, т.е. стержень уже можно считать точечным зарядом.
Напряженность электрического поля – это его силовая характеристика, векторная величина, определяемая отношением силы, действующей на заряд в данной точке поля, к величине заряда.
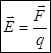
Размерность 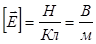 .
.
Концепция дальнодействия заключается в том, что при изменении положения одного заряда относительно другого заряда сила взаимодействия изменяется мгновенно.
Концепция близкодействия. При изменении положения одного заряда относительно другого сила взаимодействия изменяется с конечной скоростью (в вакууме – со скоростью света). Взаимодействие осуществляется при помощи посредника – электрического поля, создаваемого зарядами. Это концепция современной физики. Она пришла на смену концепции дальнодействия.
Принцип суперпозиции электрических полей. Как следует из опыта, сила, действующая на некоторый заряд со стороны системы зарядов, равна векторной сумме сил, с которыми каждый из зарядов системы действует на данный заряд 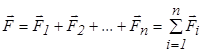 . Поделив последнее выражение на величину заряда, получим:
. Поделив последнее выражение на величину заряда, получим: 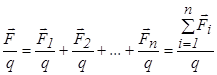 .
.
Из определения напряженности следует
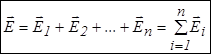
Принцип суперпозиции электрических полей: напряженность поля, создаваемого системой зарядов в некоторой точке, равна векторной сумме напряженностей, создаваемых в отдельности каждым зарядом системы в данной точке.
Напряженность электрического поля, создаваемого точечным неподвижным зарядом в некоторой точке на расстоянии 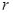 от него, можно получить с помощью закона Кулона:
от него, можно получить с помощью закона Кулона:
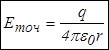
Силовые линии. Для наглядности электрические поля изображают с помощью силовых линий, т.е. воображаемых линий, в каждой точке которых напряженность 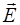 направлена по касательной. На рисунке 16.3 изображены картины силовых линий для некоторых случаев:
направлена по касательной. На рисунке 16.3 изображены картины силовых линий для некоторых случаев:
 | |||
| а) | б) | в) | г) |
| Рис. 16.3 |
а) и б) – одиночные заряды разных знаков,
в) система двух разноименных зарядов,
г) система двух одноименных зарядов.
2. Поток напряженности электрического поля. Потоком напряженности 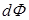 электрического поля через некоторую площадку
электрического поля через некоторую площадку 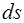 (рис.16.4) называется скалярное произведение вектора
(рис.16.4) называется скалярное произведение вектора 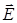 на вектор
на вектор 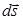
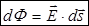
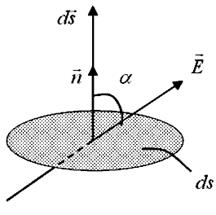 | Вектор 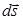 по модулю равен по модулю равен 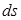 ( ( 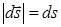 ), направлен по нормали ), направлен по нормали 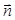 к площадке к площадке 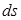 и называется вектором элементарной площадки ( и называется вектором элементарной площадки ( 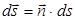 ). По правилу скалярного произведения ). По правилу скалярного произведения 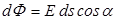 . Полный поток через произвольную поверхность конечных размеров . Полный поток через произвольную поверхность конечных размеров 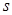 находится интегрированием по поверхности: находится интегрированием по поверхности: 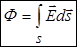 |
| Рис. 16.4 |
Теорема Гаусса (Карл Гаусс – великий немецкий математик, 1777 – 1855 гг.). Постановка задачи: имеется система точечных зарядов, которые заключены в замкнутую поверхность произвольной формы 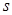 . Требуется найти поток напряженности через эту поверхность.
. Требуется найти поток напряженности через эту поверхность.
Сначала рассмотрим случай, когда внутри поверхности находится один заряд (рис.16.5). Найдем элементарный поток 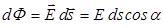 . Напряженность поля точечного заряда в некоторой точке . Напряженность поля точечного заряда в некоторой точке 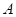 на поверхности на поверхности 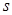 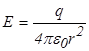 . Из рисунка видно, что . Из рисунка видно, что  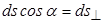 , где , где 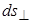 - элементарная площадка, расположенная перпендикулярно радиус-вектору, проведенному из точки расположения заряда - элементарная площадка, расположенная перпендикулярно радиус-вектору, проведенному из точки расположения заряда 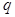 в точку в точку 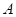 . . | 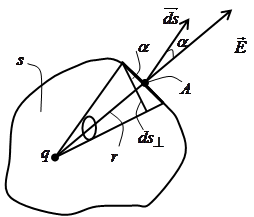 |
| Рис. 16.5 |
Тогда элементарный поток напряженности 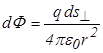 .
.
Отношение 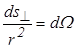 - элементарный телесный (пространственный) угол.
- элементарный телесный (пространственный) угол.
Найдем полный поток напряженности через поверхность 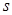 , когда внутри нее один точечный заряд:
, когда внутри нее один точечный заряд: 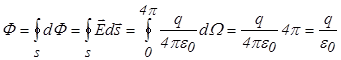 . Обобщим этот результат на случай произвольного числа зарядов внутри поверхности (рис.16.6).
. Обобщим этот результат на случай произвольного числа зарядов внутри поверхности (рис.16.6).
Воспользуемся принципом суперпозиции 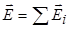 , тогда, используя то, что интеграл суммы равен сумме интегралов, получим
, тогда, используя то, что интеграл суммы равен сумме интегралов, получим
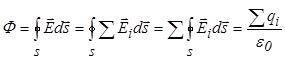 . Таким образом, . Таким образом, 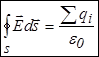 | 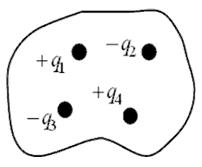 |
| Рис. 16.6 |
Теорема Гаусса.Поток вектора напряженности электрического поля через замкнутую поверхность равен алгебраической сумме зарядов, охватываемых этой поверхностью, деленной на электрическую постоянную.
«Алгебраическая сумма» означает, что каждый заряд берется со своим знаком («+» или «-»).
3. Применение теоремы Гаусса.
а) Поле бесконечной заряженной плоскости (рис. 16.7)
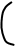   | Введем поверхностную плотность заряда 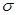 ( ( 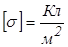 ). Выбираем вспомогательную гауссову поверхность ). Выбираем вспомогательную гауссову поверхность 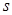 , в данном случае в виде цилиндра, основания которого параллельны плоскости, а образующие перпендикулярны ей. Записываем теорему Гаусса , в данном случае в виде цилиндра, основания которого параллельны плоскости, а образующие перпендикулярны ей. Записываем теорему Гаусса 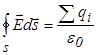 . . |
| Рис. 16.7 |
Раскладываем интеграл по поверхности на 3 интеграла (по левому основанию, правому основанию и боковой поверхности): 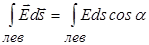 . Угол
. Угол 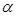 между
между 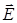 и
и 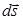 для левого основания равен нулю, значит
для левого основания равен нулю, значит 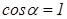 , т.е.
, т.е. 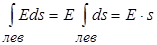 .
.
Аналогичный результат мы получим и для правого основания. Поток напряженности через боковую поверхность равен нулю (угол 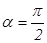 ,
, 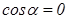 ; силовые линии параллельны боковой поверхности, ее не пересекают).
; силовые линии параллельны боковой поверхности, ее не пересекают).
Заряд, вырезаемый гауссовой цилиндрической поверхностью на заряженной плоскости, равен 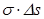 . Тогда, подставляя полученное выражение в теорему Гаусса, получим
. Тогда, подставляя полученное выражение в теорему Гаусса, получим 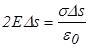 , откуда напряженность поля заряженной плоскости равна
, откуда напряженность поля заряженной плоскости равна
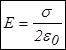
б) Поле плоского конденсатора.
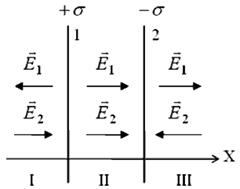 | Имеется две бесконечные заряженные плоскости, заряженные разноименно с поверхностной плотностью заряда 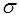 (рис. 16.8). Воспользуемся принципом суперпозиции. Напряженность поля в области I: (рис. 16.8). Воспользуемся принципом суперпозиции. Напряженность поля в области I: 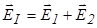 , где , где 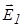 и и 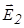 - напряженности полей, создаваемых пластинами 1 и 2 соответственно. В проекции на ось X - напряженности полей, создаваемых пластинами 1 и 2 соответственно. В проекции на ось X 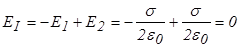 . . |
| Рис. 16.8 |
В области II 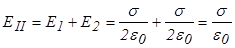 .
.
В области III 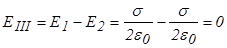 .
.
Таким образом, поле бесконечного плоского конденсатора сосредоточено внутри, между его пластинами, и равно
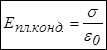
(Примечание: конденсатор можно считать бесконечным, если размеры пластин примерно на порядок больше расстояния между ними.)
в) Поле объемно-заряженного шара.
Пусть имеется равномерное скопление зарядов в виде шара (рис. 16.9) радиусом 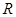 с объемной плотностью
с объемной плотностью 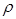 (
( 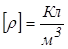 ). Поле шара обладает центральной симметрией. Записываем теорему Гаусса
). Поле шара обладает центральной симметрией. Записываем теорему Гаусса 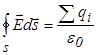 . Проведем внутри шара вспомогательную (гауссову) поверхность в форме сферы радиусом
. Проведем внутри шара вспомогательную (гауссову) поверхность в форме сферы радиусом 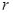 . Дальнейшие преобразования:
. Дальнейшие преобразования: 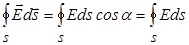 . Напряженность по величине на одном и том же расстоянии
. Напряженность по величине на одном и том же расстоянии 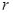 от центра шара одинакова, поэтому, вынося
от центра шара одинакова, поэтому, вынося 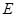 за знак интеграла, получим:
за знак интеграла, получим:
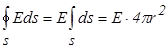 , где
, где 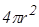 - площадь гауссовой сферы.
- площадь гауссовой сферы.
Заряд, охватываемый гауссовой поверхностью, равен 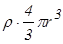 , где
, где 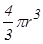 - объем шара.
- объем шара.
В итоге, подставляя в теорему Гаусса, получаем 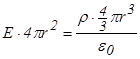 , и поле внутри заряженной сферы , и поле внутри заряженной сферы 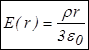 | 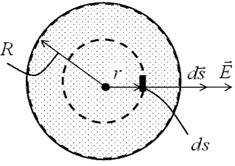 |
| Рис. 16.9 | |
Проведя аналогичные действия вне заряженной сферы, нетрудно получить 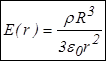 График зависимости График зависимости 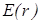 представлен на рис. 16.10. представлен на рис. 16.10. | 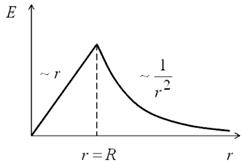 |
| Рис. 16.10 |
4. Работа сил электростатического поля.Работа силы 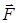 , совершаемая при перемещении
, совершаемая при перемещении 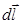 материальной точки под действием этой силы равна
материальной точки под действием этой силы равна 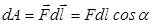 , где
, где 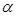 - угол между направлением силы и направлением перемещения.
- угол между направлением силы и направлением перемещения.
Пользуясь этой формулой можно найти работу по перемещению заряда в поле другого неподвижного заряда (рис. 17.1) Заряд 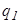 перемещается из точки 1 в точку 2 в поле заряда перемещается из точки 1 в точку 2 в поле заряда 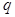 . Элементарная работа силы . Элементарная работа силы 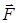 на перемещении на перемещении 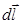 равна: равна: 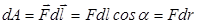 . Так как сила . Так как сила 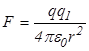 , то полная работа на пути из точки 1 в точку 2 равна , то полная работа на пути из точки 1 в точку 2 равна 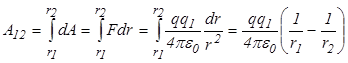 , то есть: , то есть: |  |
| Рис. 17.1 |

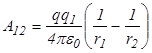 (*)
(*)