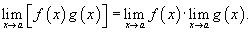Числовые последовательности. Определение. Что такое ограниченная неограниченная последовательность

Числовая последовательность — это последовательность элементов числового пространства

Определение: Пусть множество X — это либо множество вещественных чисел R, тогда последовательность 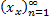элементов множества X называется числовой последовательностью.

Ограниченная и неограниченная последовательность.

Последовательность {xn} называется ограниченной, если существует такое число М>0, что для любого n верно неравенство: 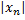<M т.е. все члены последовательности принадлежат промежутку (-М; M).

Последовательность {xn} называется ограниченной сверху, если для любого n существует такое число М, что xn ≤ M.

Последовательность {xn} называется ограниченной снизу, если для любого n существует такое число М, что xn ≥ M

Предел числовой последовательности. Теорема. Свойства предела.

Число а называется пределом последовательности {xn}, если для любого положительного >0 существует такой номер N, что для всех n > N выполняется условие: Это записывается: lim xn = a.

В этом случае говорят, что последовательность {xn}сходится к а при n→∞.

Свойство: Если отбросить какое- либо число членов последовательности, то получаются новые последовательности, при этом если сходится одна из них, то сходится и другая.

Пример. Доказать, что предел последовательности lim 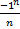= 0

Пусть при n > N верно 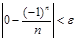, т.е. 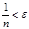. Это верно при 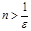, таким образом, если за N взять целую часть от 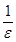, то утверждение, приведенное выше, выполняется.

Пример. Показать, что при n →∞ последовательность 3, 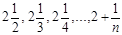имеет пределом число 2.

Итого: {xn}= 2 + 1/n; 1/n = xn – 2

Очевидно, что существует такое число n, что 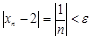, т.е. lim {xn} = 2.

Теорема. Последовательность не может иметь более одного предела.

Теорема. Если (xn)→ a, то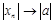

Теорема. Если (xn) → a, то последовательность {xn} ограничена.

Предел функции и его свойства. Односторонние пределы.

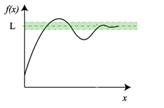
Предел функции — одно из основных понятий математического анализа. Функция f(x) имеет предел L в точке x0, если для всех значений x, достаточно близких к x0, значение f(x) близко к L.

Предел функции на бесконечности описывает поведение значения данной функции, когда её аргумент становится бесконечно большим (по абсолютной величине).

Предел функции обозначается как .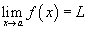

Свойства пределов функции

1) Предел постоянной величины

Предел постоянной величины равен самой постоянной величине:

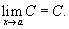
2) Предел суммы

Предел суммы двух функций равен сумме пределов этих функций:

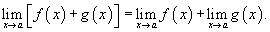
Аналогично предел разности двух функций равен разности пределов этих функций.

Расширенное свойство предела суммы:

Предел суммы нескольких функций равен сумме пределов этих функций:

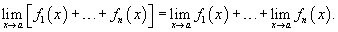
Аналогично предел разности нескольких функций равен разности пределов этих функций.

3) Предел произведения функции на постоянную величину

Постоянный коэффициэнт можно выносить за знак предела:

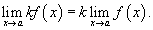
4) Предел произведения

Предел произведения двух функций равен произведению пределов этих функций: