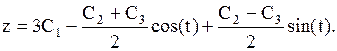Системы дифференциальных уравнений

Практическое занятие №1

Системы обыкновенных дифференциальных уравнений. Основные свойства. Фазовые траектории.

Системы дифференциальных уравнений

Для решения многих технических и экономических задач требуется определить несколько функций. Нахождение этих функций может привести к нескольким ДУ, образующим систему.

Определение 1.32 Системой ДУназывается совокупность ДУ, каждое из которых содержит независимую переменную x, искомые функции y₁, y₂,…,y_n и их производные.

Общий вид системы ДУ первого порядка, содержащей n искомых функций y₁, y₂,…,y_n

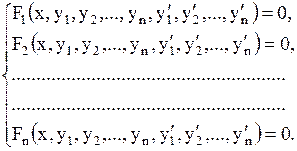
Определение 1.33 Нормальной системой ДУназывается система ДУ первого порядка, разрешенных относительно производной

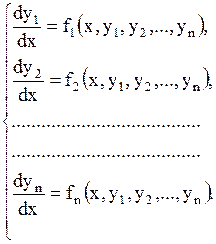(1.58)

Число уравнений системы равно числу искомых функций. Системы ДУ и ДУ высших порядков во многих случаях можно привести к нормальной системе ДУ (1.58).

Например, система трех ДУ второго порядка

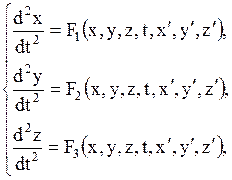
путем введения новых переменных 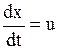, , 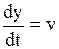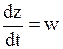приводится к нормальной системе ДУ:

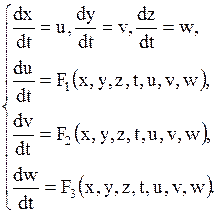
Определение 1.34 Решением системы(1.58) называется совокупность из n функций 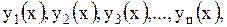которые после подстановки в систему обращают каждое её уравнение в верное равенство.

Определение 1.35 Начальными условиями для системы (1.58) называется условия вида

,

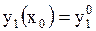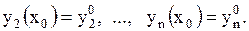(1.59)

Определение 1.36 Решением задачи Коши для системы (1.58) называется такое решение, которое удовлетворяет начальным условиям (1.59).

Определение 1.37 Общим решением системы (1.58) в области D называется набор функций 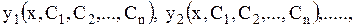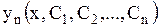, которые для любых 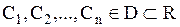являются решением (1.58) и для любых начальных условий (1.59) из области определения системы существует набор 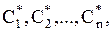при котором функции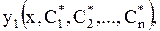 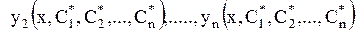удовлетворяют начальным условиям (1.59).

Определение 1.38 Всякое решение

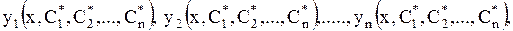(1.60)

полученное из общего решения

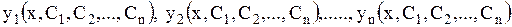(1.61)

при начальных условиях (1.59), называется частным решением.

Одним из методов решения нормальной системы ДУ является метод сведения системы к одному ДУ высшего порядка.

Пусть задана система (1.58). Продифференцируем по x любое, например первое, уравнение:

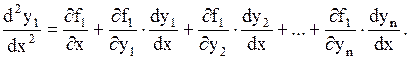(1.62)

Подставив в это равенство производные 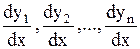из системы (1.58), получим 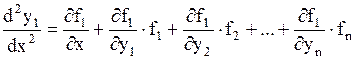, или

.

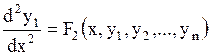(1.63)

Продифференцировав равенство (1.63) ещё раз и заменив 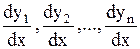из (1.58), получим

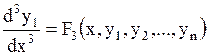(1.64)

и так далее.

Продифференцировав (1.63) в последний раз, получаем

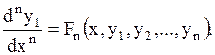(1.65)

Система из полученных уравнений имеет вид:

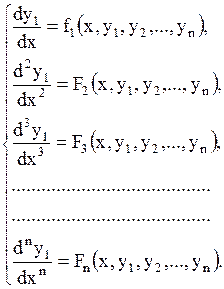(1.66)

Из первых (n-1) уравнений системы (1.66) выразим функции y₂,y₃,…,y_n через x, функцию y₁ и её производные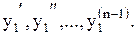

Получим:

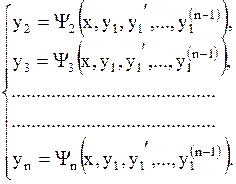(1.67)

Найденные значения y₂,y₃,…,y_n подставим в последнее уравнение системы (1.67). Получим одно ДУ n-го порядка относительно искомой функции y₁:

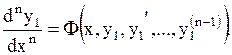(1.68)

Пусть его общее решение есть функция

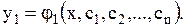(1.69)

Продифференцировав его (n-1) раз и подставив значения производных 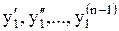в уравнения системы (1.67), найдем функции :

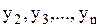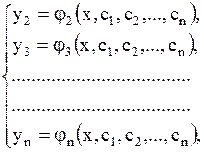(1.70)

Пример 1.31Решить систему дифференциальных уравнений

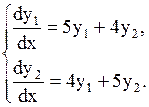
Решение. Дифференцируем первое уравнение по x:

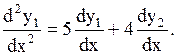(1.71)

Из первого уравнения системы определяем 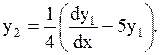Тогда из второго уравнения системы имеем

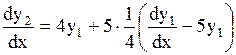, т.е.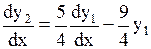

Подставляя полученное для 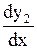выражение в соотношение (1.71), имеем

.

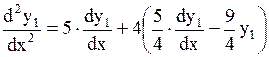Таким образом, приходим к уравнению второго порядка с одной неизвестной функцией :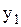

.

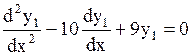Решая его, находим

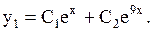
Тогда

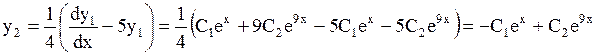
Итак, общее решение системы имеет вид

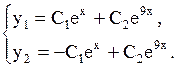
Рассмотрим еще один метод решения нормальной системы ДУ (1.58), когда она представляет собой систему линейных однородных ДУ с постоянными коэффициентами, т.е. систему вида

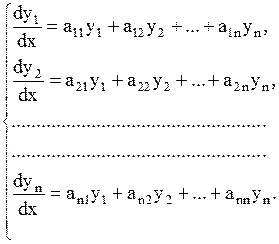(1.72)

Для простоты рассмотрим систему трех уравнений с тремя неизвестными функциями y₁,y₂,y₃:

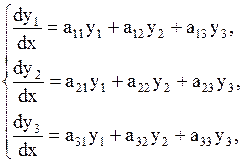(1.73)

где 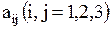- постоянные коэффициенты.

Будем искать частное решение системы (1.73) в виде

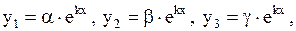(1.74)

где 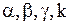- постоянные, которые надо подобрать так, чтобы функции (1.74) удовлетворяли системе (1.73).

Подставив эти функции в систему (1.73) и сократив на множитель , получаем:

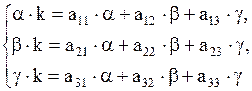
или

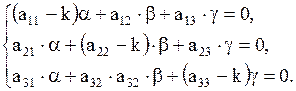(1.75)

Система (1.75) – однородная система линейных алгебраических уравнений с тремя неизвестными 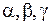имеет ненулевые решения тогда и только тогда, когда определитель системы равен нулю:

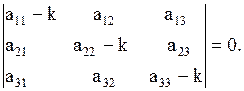(1.76)

Определение 1.39Уравнение (1.76) называется характеристическим уравнением системы (1.73).

Уравнение (1.76) является уравнением третьей степени относительно k. Рассмотрим возможные случаи.

Случай 1. Корни (1.76) действительные и различные 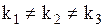. Для каждого корня 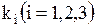напишем систему (1.75) и определим коэффициенты 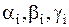(один из коэффициентов можно считать равным единице).

Получаем частные решения системы (1.73):

для корня : , , ;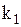

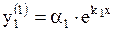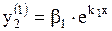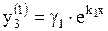для корня : , , ;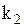

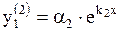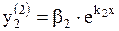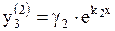для корня : , , .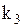

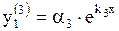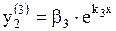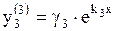Эти функции образуют фундаментальную систему решений и общее решение системы (1.73) записываются в виде:

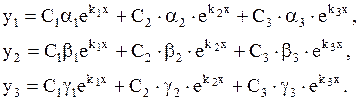(1.77)

Случай 2.Характеристическое уравнение (1.76) имеет корень k кратности m (m=2;3). Решение системы, соответствующее кратному корню, ищем в виде:

а) если m=2, то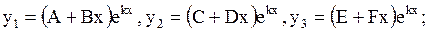

б) если m=3, то , , .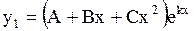

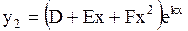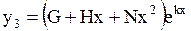Это решение зависит от m произвольных постоянных A, B, C,…, N, которые определяются методом неопределенных коэффициентов. Выразив все коэффициенты через m из них, полагаем поочередно один из них равным единице, а остальные равными нулю. Получим m линейно независимых частных решений системы (1.73).

Случай 3.Корни характеристического уравнения различные, но среди них есть комплексные: 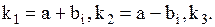Вид частных решений:

для k₁: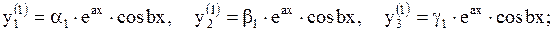

для k₂: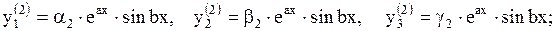

для k₃: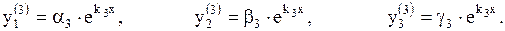

Общее решение имеет вид:

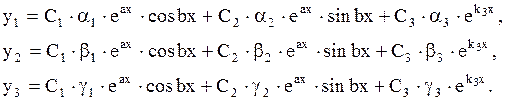(1.78)

Пример 1.32Решить систему уравнений:

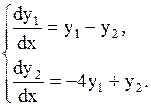
Решение. Характеристическое уравнение имеет вид 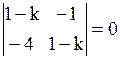, его корни k₁= –1, k₂=3.

Частные решения ищем в виде 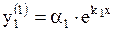, 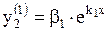и 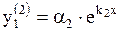, 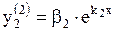. Найдем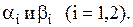

При k₁= –1 система (1.75) имеет вид

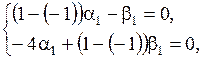или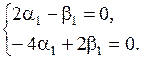

Эта система имеет бесчисленное множество решений. Пусть 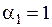, тогда 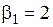. Получаем частные решения , .

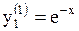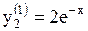При k₂=3 система (1.75) имеет вид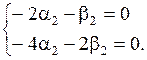

Пусть 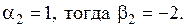Тогда корню k₂=3 соответствуют частные решения: 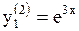и .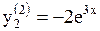

Общее решение исходной системы 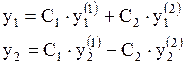имеет вид: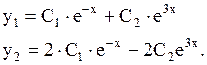

Самостоятельная работа

1. Найти общее решение системы уравнений: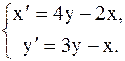

Отв.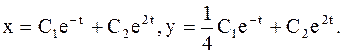

2. Найти решение задачи Коши: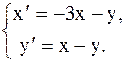

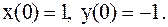
Отв.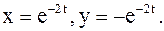

3. Найти общее решение системы уравнений

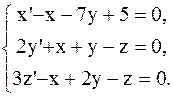
Отв.