I. требования к оформлению эпюра

МЕТОДИЧЕСКИЕ УКАЗАНИЯ И

ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ

К ЭПЮРАМ

ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ

Благовещенск

Издательство ДальГАУ

2012

УДК 514. 18 (072)

Работа “ Методические указания к эпюрам по начертательной геометрии “ выполнена преподавателями кафедры “Основы констру-ирования и графики” Паньковой Т.Л., Ивановым С.А., Дерезиной Е.В.

Методические указания предназначены для выполнения студентами первого курса инженерных специальностей .

Содержание работы соответствует требованиям государственного образовательного стандарта и рабочей программе. В данные методические указания включены задания к трем графическим самостоятельным работам (эпюрам), цель выполнения которых - углубить знания, полученные на теоретических занятиях по начертательной геометрии.

Методические указания содержат рекомендации по выполнению и

оформлению графических работ в соответствии с ГОСТами, а также примеры выполнения чертежей.

Рецензент : д.т.н., профессор Щитов С.В.

Методическая разработка “ Методические указания к эпюрам по на-чертательной геометрии “ рекомендованы к печати в издательстве ДальГАУ с присвоением грифа “Дальневосточный государственный аграрный университет” методическим советом института механизации сельского хозяйства. Протокол № 1 от сентября 2011 года

Издательство ДальГАУ

ВВЕДЕНИЕ

Задания, находящиеся в данном сборнике, предназначены для само-стоятельного выполнения студентами по мере освоения курса начерта-тельной геометрии с целью закрепления изученного материала.

Сборник содержит три комплексных задания (три эпюра), решение которых требует знания основных разделов курса.

I. ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ ЭПЮРА

Каждое задание выполняется карандашом на отдельном листе чертеж-ной бумаги указанного формата. Построения выполнять аккуратно с помощью чертежных инструментов по ГОСТ 2.303-68 «ЛИНИИ» (толщину сплошных основных линий следует принять равной 0,8 мм, толщину сплошных тонких и штриховых линий 0,4 мм). Все надписи должны выполняться в соответствии с требованиями ГОСТ 2.304-81 «ШРИФТ» шрифтом типа Б либо с наклоном к основанию строки 75^о, либо без наклона. Минимальный размер шрифта 3,5 мм.

В правом нижнем углу каждого формата следует располагать основную надпись для учебных целей (рис.1).

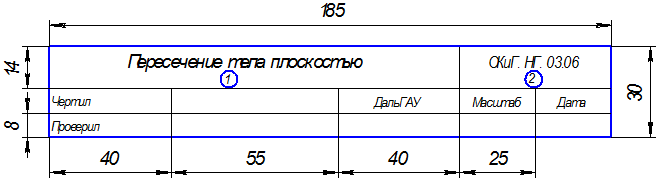
Рис.1. Основная надпись

В графе 1 основной надписи указывается тема выполненного задания.

В графе 2 указывается буквенно-цифровой код задания, например, ОКиГ.НГ.03.06,

где ОКиГ.НГ. - кафедра основ конструирования и графики,

начертательная геометрия,

03 – порядковый номер задания,

06 – номер варианта задания.

Задания должны быть сброшюрованы в альбом и снабжены титульным листом формата А3 горизонтального расположения, выполненным от руки (рис.2).

ДАЛЬНЕВОСТОЧНЫЙ ГОСУДАРСТВЕННЫЙ

АГРАРНЫЙ УНИВЕРСИТЕТ

ИНСТИТУТ МЕХАНИЗАЦИИ СЕЛЬСКОГО ХОЗЯЙСТВА

Кафедра “Основы конструирования и графики”

КОНТРОЛЬНАЯ РАБОТА

ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ

И ИНЖЕНЕРНОЙ ГРАФИКЕ

Выполнил : Ф. И. О. студента,

группа

Проверил : Ф. И. О. преподавателя

Благовещенск, 2012

Рис.2.Титульный лист

2 ЭПЮР № 1

Содержание задания

По координатам точек А,В,С,D,Е построить плоскость ∆ АВС и:

1. Определить в миллиметрах расстояние от точки D до плоскости треугольника АВС; определить видимость перпендикуляра, проходящего через точку D к плоскости треугольника АВС.

2. Построить плоскость, параллельную плоскости треугольника АВС и удаленную от нее на расстояние 50 мм;

3. Через прямую DE провести плоскость, перпендикулярную плоскости треугольника АВС; построить линию пересечения этих двух плоскостей; определить видимость.

Методические указания

Эпюр №1 включает в себя три задачи. Рассмотрим последовательно алгоритм их решения.

Задача № 1. Для того, чтобы определить расстояние от точки D до плос-кости треугольника АВС, необходимо опустить перпендикуляр из точки D на плоскость треугольника АВС, используя горизонталь и фронталь плоскости, и найти точку пересечения этого перпендикуляра с плоскостью треугольника АВС (это будет точка К, основание перпендикуляра).

Горизонтальную проекцию перпендикуляра к плоскости проводим перпендикулярно горизонтальной проекции горизонтали (горизонталь А1, на рисунке 3 ее проекции обозначены а1, а^' 1^' ) .

Фронтальную проекцию перпендикуляра к плоскости проводим перпендикулярно фронтальной проекции фронтали (фронталь – С2, ее проекции с2, с^' 2^' ).

Чтобы найти точку К, необходимо:

- через перпендикуляр провести вспомогательную проецирующую плоскость (в примере это плоскость γ);

- построить линию пересечения заданной и вспомогательной плоскостей (линия MN);

- найти точку пересечения перпендикуляра с линией MN (точка К).

Затем определим истинную величину перпендикуляра DK способом прямоугольного треугольника. Натуральная величина отрезка DK построена на плоскости H (треугольник D_o d k на рисунке 3 ). Отрезок DK есть гипотенуза прямоугольного треугольника, один катет которого – отрезок dk ,

а второй катет – разница в координатах Zмежду точками D и K (ΔZ).

Видимость проекций перпендикуляра определим методом кон-курирующих точек. Видимость на плоскости Н определена с помощью конкурирующих точек М и 3. Поскольку у точки 3 больше координата Z, то она закрывает точку М на виде сверху. Видимость на плоскости V определена с помощью конкурирующих точек 4 и 5. Поскольку у точки 5 больше координата Y, то она закрывает точку 4 на виде спереди.

Задача № 2.Плоскость, параллельную треугольнику АВС, можно задать двумя пересекающимися прямыми, параллельными двум сторонам треугольника АВС.

Из точки А проводим перпендикуляр к плоскости треугольника АВС (АF, точка F выбрана произвольно). Находим натуральную величину отрезка AF , для чего строим прямоугольный треугольник, гипотенуза которого – натуральная величина отрезка AF. На натуральной величине отрезка AF от точки А_о отмеряем 50 мм (точка L_о). Данную точку находим на проекциях отрезка АF ( l, l’) . Из этих точек строим две проекции искомой плоскости. Прямая М₁ ( ее проекции m₁ , m₁^' ) проведена параллельно стороне ВС. Прямая М₂ проведена параллельно стороне АС ( ее проекции m_{2 ,} m₂ ^' ).

Примечание: для решения задачи №2 можно использовать перпендикуляр к плоскости треугольника АВС, отмерив на его натуральной величине 50 мм.

Задача № 3.Строим плоскость, перпендикулярную заданной треу-гольником АВС, соблюдая условие перпендикулярности плоскостей. Иско-мую плоскость можно задавать двумя пересекающимися прямыми, одна из которых должна быть перпендикулярна плоскости треугольника АВС. В задаче № 1 мы построили перпендикуляр к плоскости ∆ ABC, поэтому плоскость зададим отрезком DE и перпендикуляром. Затем найдем линию пересечения двух плоскостей. Линия пересечения двух плоскостей строится по двум общим точкам, одна из которых – точка пересечения перпенди-куляра с плоскостью треугольника АВС (это точка К), а вторая – точка пересечения отрезка DE с плоскостью треугольника АВС (это точка К₁).

Для нахождения точки К₁ необходимо:

- через DE провести вспомогательную плоскость ( на рисунке 3 это горизонтально-проецирующая плоскость α);

- построить линию пересечения вспомогательной плоскости с плоскостью треугольника АВС ( это линия M₁ N₁);

- найти точку пересечения отрезка m₁'n'₁ c e'd' ( это точка f ' ).

Соединяем точки K и F (в двух проекциях это отрезки fk и f'k' ). В пересечении линии FK со стороной АВ получаем точку K ₁. Искомая линия пересечения двух плоскостей – линия KK₁ ( в проекциях k k₁ , k 'k'₁ ).