Охарактеризуйте свойства симметрического линейного оператора
1) Линейный оператор является симметрическим тогда и только тогда, когда его матрица в любом ортонормированном базисе симметрична, т.е. совпадает с транспонированной матрицей оператора.
2) Собственные векторы симметрического линейного оператора, отвечающие различным собственным числам, ортогональны.
3) Собственному числу кратности m симметрического линейного оператора соответствует линейно независимая система из m собственных векторов этого оператора.
4) Для всякого симметрического линейного оператора (симметричной матрицы) существует ортонормированный базис, состоящий из его собственных векторов.
131. Дать определение линейной формы L[y].
Отображение 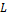 линейного пространства
линейного пространства 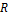 во множество вещественных чисел называется линейной формой или линейным функционалом, если для любых векторов
во множество вещественных чисел называется линейной формой или линейным функционалом, если для любых векторов 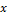 и
и 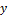 из
из 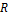 и любых чисел
и любых чисел 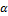 и
и 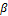 выполняется условие:
выполняется условие:
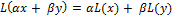
132. Запишите общий вид линейной формы. Как вычисляются коэффициенты линейной формы?
Общий вид линейной формы:
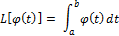
Коэффициенты линейной формы подбираются следующим образом: каждый 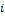 -тый коэффициент является
-тый коэффициент является 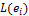 , где
, где 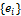 – базис.
– базис.
133. Как изменяются коэффициенты линейной формы при изменении базиса?
Коэффициенты линейной формы преобразуются по тому же закону, что и базисные векторы.
134. Дать определение билинейной формы В( 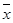 ,
, 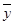 ).
).
Билинейная форма – функция 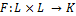 , линейная каждому из аргументов:
, линейная каждому из аргументов:
1) 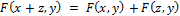 ;
;
2) 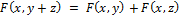 ;
;
3) 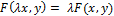 ;
;
4) 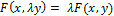 ,
,
где 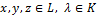 .
.
Матрица билинейной формы:
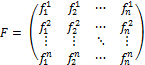
Билинейная форма действует на аргументы:
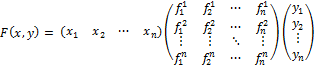
135. Запишите общий вид билинейной формы. Как определяются элементы матрицы билинейной формы?
Общий вид билинейной формы:
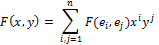
Элементы матрицы билинейной формы определяются следующим образом:
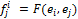
136. Какая билинейная форма называется симметричной?
Билинейная форма называется симметричной, если можно поменять аргументы местами и это не повлияет на результат.
137. Как изменяется матрица билинейной формы при изменении базиса?
Матрица, представляющая билинейную форму в новом базисе, связана с матрицей, представляющей её в старом базисе, через матрицу, обратную матрице перехода к новому базису (матрице Якоби), через которую преобразуются координаты векторов.
Иными словами, если координаты вектора в старом базисе 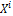 выражаются через координаты в новом
выражаются через координаты в новом  через матрицу
через матрицу 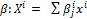 , или в матричной записи
, или в матричной записи 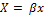 , то билинейная форма
, то билинейная форма 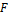 на любых векторах
на любых векторах 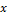 и
и 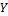 запишется, как
запишется, как
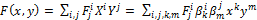 ,
,
то есть компоненты матрицы, представляющей билинейную форму в новом базисе, будут:
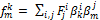 ,
,
или, в матричной записи:
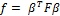 ,
,
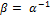 ,
,
где 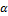 — матрица прямого преобразования координат
— матрица прямого преобразования координат 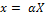 .
.
138. Дать определение квадратичной формы. Запишите общий вид квадратичной формы при n=3.
Квадратичная форма – функция, определённая в евклидовом пространстве 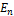 соотношением
соотношением 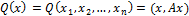 , где матрица
, где матрица 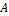 – симметрическая. Общий вид:
– симметрическая. Общий вид:
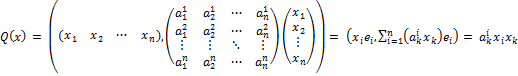 ,
,
Где 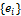 – некоторый ортонормированный базис в
– некоторый ортонормированный базис в 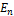 и
и 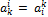 . При
. При 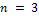 :
: