Пикар әдісі

Бұл y^/=f(x,y) (1) диффенерциалды теңдеуді аналитикалық функция түрінде жақындатылған шешімін алуға мүмкіндік береді. Пикар әдісі (1) теңдеудің жалғыз шешімінің және табылу теоремасын дәлделдеуге байланысты пайда болады және мәні бойынша сығылған көріністің принципін қолданудың бірі болып табылады. Бастапқы (2) шарты бар (1) теңдеуінің шешімін табу теоремасының шартына сәйкес табу талап етілсін (1) теңдеуінің екі жағын x₀-ден x-ке дейін интегралдаймыз:

y(x₀)=y₀ (5)

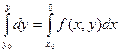
немесе

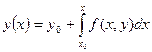(5)

(5) интегралды теңдеу шешімі дифференциалды теңдеуді және бастапқы шартты қанағаттандырады.

Шынында да, x=x₀ кезінде аламыз:

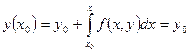
Сонымен (5) интегралдың теңдеудің шешімі тізбекті жақындау әдісін қолдануға мүмкіндік береді. y=y₀ теңестіріп (5) теңдеуінен бірінші жақындауды аламыз:

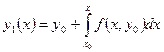
Оң жақтағы интеграл тек x айнымалысынан тұрады, бұл интегралды тапқаннан кейін y₁(x) жақындаудың аналитикалық өрнегі x айнымалы функциясы сияқты алынады. Енді (5) теңдеуінде у-те табылған у₁(х) мәнімен алмастырамыз және екінші жақындауды аламыз;

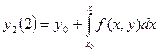
Және тағы сол сияқты.

Жалпы жағдайда интеграциялық формула мынадай түрде блады:

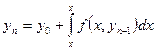
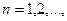(6)

(6) формуланың циклдық қолдануы төмендегі функция тізбегін береді:

Y₁(x), y₂(x), …, y_n(x) (7)

G-облысында f функциясы үзіліссіз болғандықтан, онда ол функция (х₀, у₀) нүктесінен тұратын кейбір 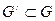облысында шектеулі болады, яғни

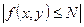(8)

Табылу теоремасы жағдайында (6) теңдеуіне қысылған көріністер принципін қолдана отырып (7) тізбегінің сәйкес келетін ( 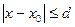сегментінде анықталған φ кеңістіктегі φ үзіліссіз функциялар ρ(φ₁, φ₂)=max │φ₁(x)-φ₂(x)│ метрикасы бойынша сәйкестік түріне айналады) көрсету қиын емес. Оның шегі интегралдық теңдеу шешімі яғни (2) бастапқы шарты бар диффенерциалдық теңдеу шешімі болып табылады. Бұл (7) тезбегінің R-ші мүшесі анықталған нақталық дәрежесі бар (1) теңдеуінің нақты шешіміне жақындау болып табылады. R–ші жақындау қателігін бағалау төмендегі формуламен беріледі:

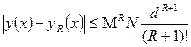(9)

Мұнда М – Липшиц константасы (4) N- (8) теңсіздігіндегі f функциясының моділінің жоғарғы шегі, ал 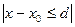аралығын анықтау үшін d шамасы төмендегі формула бойынша есептеледі.

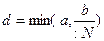. (10)

12.3. Біртіндеп жуықтау әдісі

Коши есебін қарастырайық. Біртіндеп жуықтау әдісі бойынша 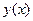шешімі 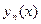функциясынын тізбектерінін шегі ретінде қарастырылады. Жоғарыда айтылған шарттар қанағаттандырылсын деп ұйғарсақ, келесі рекуренттік формула бойынша 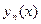табылады

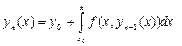(11)