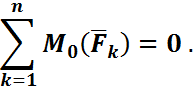Күштердің кез келген жазық жүйесінің тепе-теңдік шарты мен теңдеулері

Күштердің кез келген жазық жүйесі үшін Вариньон теоремасы

Теорема.Егер күштердіц кез келген жазъщ жүйесі тең әсер етуші күшке келтірілетін болса, онда осы тең әсер етуші күштің күштер әсер ететін жазъщтъщта жататын кез келген нүктеге қатысты моменті барлъщ қүраушы күштердің сол нүктеге қатысты моменттерінің алгебральщ қосындысына тең.

6.3,б-суретте тең әсер етуші R= R'күші Анүктесіне түсіріледі. Бұл мүкте келтіру Оцентрінен ОАқашықтығында орналасқан:

О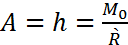
Анүктесінде түсірілген тең әсер етуші

Ккүшінің кез келген келтіру Оцентріне қатысты моментін анықтайық (6.4-сурет):

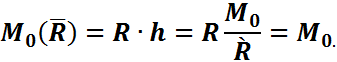
мұнда: М₀- қарастырылып отырған күштер жүйесінің келтіру Оцентріне қатысты бас моментінің абсолют шамасы. Тең әсер етуші 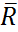күшінің келтіру Оцентріне қатысты моментінің таңбасы М₀бас моменттің немесе ( 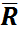, 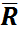”)қос күшінің (6.3,а,б-сурет) таңбасымен бірдей болады.

(6.5) теңдігі бойынша

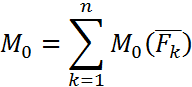
Осы теңдікті (6.9) формулаға қойсақ, тең әсер етуші күштің моменті

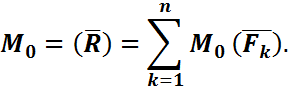
Сонымен, теорема дэлелденді.

Күштердің кез келген жазық жүйесінің тепе-теңдік шарты мен теңдеулері

Күштердің кез келген жазық жүйесінің бас векторы және бас моменті нөлге тең болса, күштер жүйесі нөлге балама болады деп жоғарыда (§6.3)айтылған болатын: 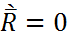, М₀=0 немесе ( 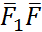₂,..., 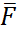_п)<=> 0. Осы тұжырым- дарға сүйене отырып, күштер жүйесінің аналитикалық түріндегі тепе- теңдік шартын тағайындайық.

1.Тепе-теңдік шартының негізгі түрі. (6.5) жэне (6.7) теңдіктерде R' және М₀ шамалары

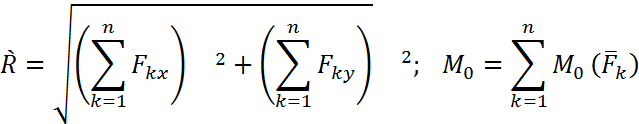
Күштер жүйесі тепе-теңдікте болғанда, Я' = 0, М₀ = 0, яғни

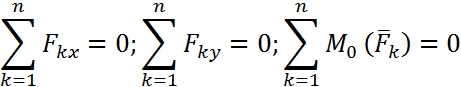
Осы жазылған формулалар күштердің кез келген жазық жүйесінің аналитикалық түріндегі тепе-теңдік теңдеулері болып табылады. Сөйтіп, күштердің кез келген жазъщ жүйесі тепе-теңдікте болуы үшін, барлық күштердің осы күштер жүйесінің әсер ету жазьщтыгында орналасқан екі координат өстеріне проекцияларының алгебралъщ қосындысы және

барлық жүйе күштерінің осы жазықтықтагы кез келген нүктеге қатысты моменттерінің алгебралық қосындысы нөлге тең болуы қажет және жеткілікті.

2.Тепе-теңдік шартының екінші түрі.

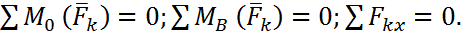(6.12)

Күштердің кез келген жазық жүйесі тепе-теңдікте болуы үшін, барлық күштердің осы күштер жүйесінің әсер ету жазықтыгында алынган кез келген екі А және В нүктелеріне қатысты моменттеріңің алгебралық қосындысы және А, В нүктелері арқылы өтетін түзуге перпендикуляр болмайтын кез келген Ох өсіне проекцияларыныц алгебралъщ ңосындысы нөлге тең болуы қажет және жеткілікті.Осы шарттардың қажеттілігі күштер жүйесі тепе-теңдікте болғанда, барлық күштердің осы күштер жүйесінің әсер ету жазықтығында алынған кез келген нүктеге қатысты моменттерінің алгебралық қосындысы мен барлық күштердің кез келген өске проекцияларының алгебралық қосындысы нөлге тең болуынан шығады. Енді осы шарттардың жеткіліктілігін дәлелдейік. Ол үшін кезекпен А жэне В нүктелерін келтіру центрі ретінде алайық.Егер қарастырылып отырған күштер жүйесі үшін (6.12) теңдеулердің алғашқы екі шарты ғана орындалатын болса, онда М_А = 0, М_в = 0. Бұл жағдайда осы күштер жүйесі 6.3-ші параграфта айтылғандай, тепе-теңдікте болмай, А және В нүктелері арқылы өтетін шамасы бас вектордың шамасына тең, тең әсер етуші К күшке келтірілуі мүмкін (6.5-сурет). Бірақ үшінші шарт бойынша

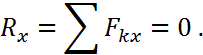
болуы қажет. Ох өсі АВ түзуіне препендикуляр болмайтын жэне кез келген жаққа бағытталатын түзу болатындықтан, соңғы шарт тек қана тең әсер етуші К күші нөлге тең болғанда ғана орындалады. Сондықтан күштердің кез келген жазық жүйесі 6.12 шарттар қанағаттандырылғанда ғана тепе-теңдікте болады.

3.Тепе-теңдік шартының үіиінші түрі.

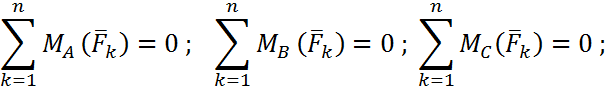
Күштердің кез келген жазъщ жүйесі тепе-теңдікте болуы үшін, барлыц күиітердің осы күштер жүйесінің әсер ету жазъщтыгында алынган бір түзудің бойында жатпайтын А, В және С нүктелеріне қатысты моменттерінің алгебралық қосындысы нөлге тең болуы қажет және жеткілікті.

Осы шарттардың қажеттілігі күштердің кез келген жазық жүйесі тепе- теңдікте болғанда, барлық күштердің осы күштер жүйесінін әсер ету жазықтығында алынған кез келген нүктеге қатысты моменттерінің алгебралық қосындысы нөлге тең болуынан туындайды. Осы шарттардың жеткілікті болатынын дәлелдейік.Келтіру центрі ретінде А нүктесін алайық. Дәлелдеуді қажет етіп отырған тұжырымның шарты бойынша