Интегралы движения в методе Гамильтона
Рассмотрим полную производную функцию обобщенных координат, обобщенных импульсов и времени  :
:

Используем уравнения движения Гамильтона  :
:

Здесь мы ввели обозначение:
 - скобки Пуассона
- скобки Пуассона
Если  , то
, то  . В этом случае мы можем сформулировать условие того, что функция
. В этом случае мы можем сформулировать условие того, что функция 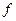 интеграл движения:
интеграл движения:
Чтобы 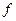 была интегралом движения, скобки Пуассона
была интегралом движения, скобки Пуассона  должны обращаться в нуль.
должны обращаться в нуль.

Скобки Пуассона и их свойства.

1. 
2. 
3. 
4. 
5. 
6. тождество Якоби 
7. 
Докажем свойство 7:

используем свойства 5 и 6:

используем свойство 1:


используем свойство 3:

Теорема Пуассона:
Пусть 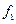 и
и  интегралы движения, это означает, что
интегралы движения, это означает, что  и
и  , тогда согласно свойству 7:
, тогда согласно свойству 7:
 =0
=0
Скобки Пуассона интегралов движения являются интегралом движения. Если мы знаем интегралы движения, то с помощью скобок Пуассона можно получать более удобные формы интегралов движения.
Рассмотрим частные случаи скобок Пуассона:
1. 

т.к.  и
и  , то
, то 
2. 
3. 

Учитывая  ,
,  ,
,  ,
,  получаем:
получаем:

4. 

5. 


6. 

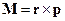 ,
,  , тогда:
, тогда:

7. 
8.  Здесь
Здесь  - компонента вектора
- компонента вектора  - функции от координат и импульсов.
- функции от координат и импульсов.
 , здесь
, здесь  - скаляр.
- скаляр.
 , здесь
, здесь  - скалярная функция координат и времени.
- скалярная функция координат и времени.
Задачи
1. Определить скобки Пуассона, составленные из декартовых компонент импульса р и момента импульса 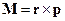 материальной частицы.
материальной частицы.
Ответ: 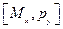 =-pz
=-pz
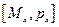 =0,
=0, 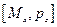 =-py
=-py
2. Определить скобки Пуассона, составленные из компонент М.
Ответ: 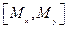 =-Mz,
=-Mz, 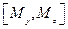 =-Mx ,
=-Mx , 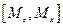 =-My.
=-My.
3. Показать, что
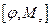 =0,
=0, 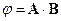 ,
,
где φ – любая скалярная функция координат и импульса частицы.
Указание. Скалярная функция может зависеть от компонент векторов r и pтолько в комбинациях r2,p2, 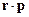 . Поэтому
. Поэтому
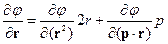
и аналогично для 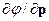 .
.
4. Показать, что
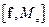 =
= 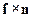 ,
,
где f – векторная функция координат и импульса частицы, а n – единичный вектор в направлении оси z.
Указание. Произвольный вектор f(r, p) может быть написан в виде 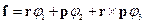 где
где 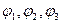 - скалярные функции
- скалярные функции
Малые колебания и свойства потенциальной энергии.

Рассмотрим систему с одной степенью свободы и исследуем функцию  на экстремумы.
на экстремумы.
 (отсюда получаем координаты точек равновесия для графика).
(отсюда получаем координаты точек равновесия для графика).


 (21.1)
(21.1)
 или
или  ;
;  ;
; 
Итак:  , т.к.
, т.к.  ,
,  ,
,  ,
,  .
.
Отбросим в (21.1) слагаемые, начиная с третьего члена - получим параболический вид потенциальной энергии.
Если потенциальная энергия возрастает при удалении от положения равновесия, то в этом случае  - точка устойчивого равновесия.
- точка устойчивого равновесия.
Рассмотрим точку 

 ,
,  - точка неустойчивого равновесия.
- точка неустойчивого равновесия.
Колебания называются малыми, если в разложении последующие члены значительно меньше первых трёх:


Колебания, удовлетворяющие этому условию, называются линейными (гармоническими). Учёт последующих членов приводит к нелинейности или ангармоничности колебаний.
