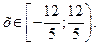Уравнение окружности, для которой высота СD является диаметром

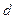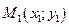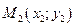Решение. 1. Расстояние между точками и определяется по формуле:

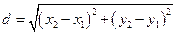. (1)

Подставив в эту формулу координаты точек А и В, имеем:

.

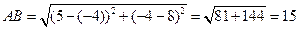2. Уравнение прямой, проходящей через точки и , имеет вид:

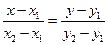. (2)

Подставив в (2) координаты точек:

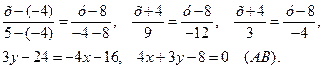
Для нахождение углового коэффициента 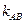прямой АВ разрешим полученное уравнение относительно у: 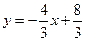. Отсюда 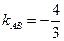. Подставив в формулу (2) координаты точек А и С, получим уравнение прямой АС.

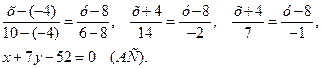
Отсюда .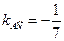

3. Угол 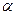между двумя прямыми, угловые коэффициенты которых равны и , определяется по формуле:

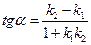. (3)

Угол А, образованный прямыми АВ и АС, найдем по формуле (3), подставив в нее , .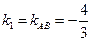

,

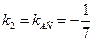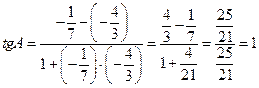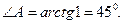
4. Так как высота 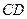перпендикулярна стороне 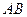, то угловые коэффициенты этих прямых обратны по величине и противоположны по знаку, т.е.

.

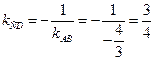Уравнение прямой, проходящей через данную точку 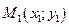в заданном угловым коэффициентом направлении, имеет вид:

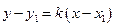. (4)

Подставив в (4) координаты точки С и 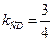, получим уравнение высоты :

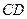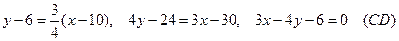. (5)

Для нахождения длины 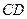определим координаты точки 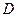, решив систему уравнений (АВ) и ( ):

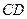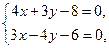
откуда 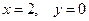, то есть .

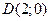Подставив в формулу (1) координаты точек С и 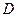, находим:

.

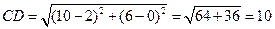5. Уравнение окружности радиуса 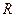с центром в точке 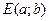имеет вид:

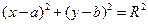. (6)

Так как 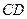является диметром искомой окружности, то ее центр Е есть середина отрезка 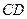. Воспользовавшись формулами деления отрезка пополам, получим:

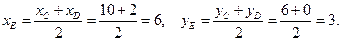
Следовательно, 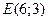и 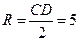. Используя формулу (6), получаем уравнение искомой окружности: .

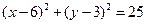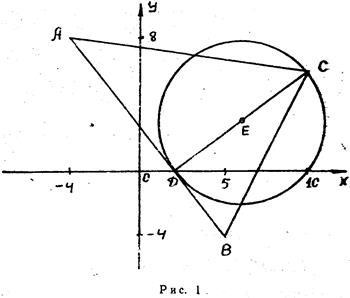
На рис. 1 в декартовой прямоугольной системе координат изображен треугольник , высота 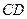, окружность с центром в точке Е.

Задача № 2. 1)Определить тип заданной кривой и построить её (для окружности указать центр, для эллипса и гиперболы – фокусы и эксцентриситет, для параболы – фокус и директрису):

x²+4y²=16.

Решение. Для того, чтобы определить тип кривой второго порядка (окружность, эллипс, гипербола или парабола), произведём преобразования заданного уравнения:

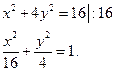
Получили каноническое уравнение эллипса:

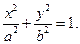
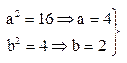
– полуоси эллипса.

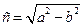
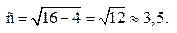Найдём координаты его фокусов: F₁(-c;0) и F₂(c;0), где – половина расстояния между фокусами.

Итак, Тогда F₁(-3,5;0) и F₂(3,5;0) – фокусы эллипса.

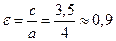– эксцентриситет эллипса:

Построим эллипс (рис. 2).

y

• •

-4 F₁ F₂ 4 х

-2

Рис. 2

2).Определить тип заданной кривой и построить её (для окружности указать центр, для эллипса и гиперболы – фокусы и эксцентриситет, для параболы – фокус и директрису):

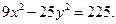
Решение. Преобразуем заданное уравнение:

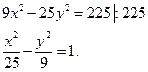
Получили каноническое уравнение гиперболы:

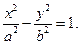
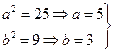
– полуоси гиперболы.

Найдём координаты её фокусов: F₁(-c;0) и F₂(c;0), где 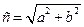– половина расстояния между фокусами.

Итак,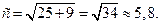

Тогда F₁(-5,8;0) и F₂(5,8;0) – фокусы гиперболы.

Эксцентриситет гиперболы: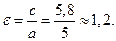

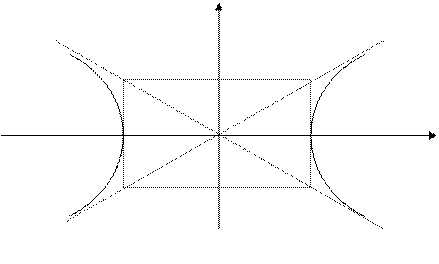
Построим гиперболу (рис. 3).

y

• •

F₁ -5 5 F₂ x

-3

Рис. 3.

3).Определить тип заданной кривой и построить её (для окружности указать центр, для эллипса и гиперболы – фокусы и эксцентриситет, для параболы – фокус и директрису).

y²=6x+12

Решение. Преобразуем данное уравнение:

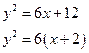
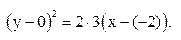Получили уравнение параболы: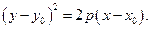

Ветви параболы направлены вправо, вершина расположена в точке (x₀; y₀), т.е. в точке (-2;0).

Для построения параболы её уравнение приведём к простейшему (каноническому) виду. Для этого произведём параллельный перенос системы координат:

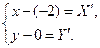
Тогда в новой системе координат X′O′Y′, где О′(-2;0) – начало координат, уравнение параболы принимает канонический вид: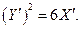

Найдём координаты фокуса и уравнение директрисы: 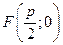– фокус, 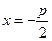– уравнение директрисы.

Итак, 2p=6, значит, р=3. Тогда F(1,5; 0) и х= -1,5.

Строим параболу в системе координат X′O′Y′ (рис.4).

y

Y^′

р

O^′ F x(X^′)

Рис.4

Задача № 3.Даны координаты трех точек: А(3; 0; –5), В(6; 2; 1), С(12; –12; 3).

Требуется:

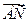1) записать векторы и в системе орт и найти их модули;

2) найти угол между векторами и ;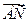

3) составить уравнение плоскости, проходящей через точку С перпендикулярно вектору .

Решение. 1) Если даны точк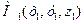и и 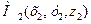, то вектор 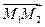через орты 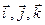выражается следующим образом:

.

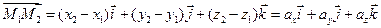Подставляя в эту формулу координаты точек А и В, имеем:

.

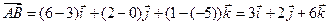Аналогично

.

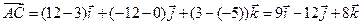Модуль вектора 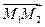вычисляется по формуле

.

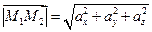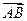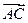Подставляя в формулу найденные ранее координаты векторов и , находим их модули:

,

.

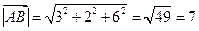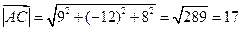2) Косинус угла 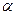, образованного векторам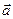и и 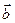, равен их скалярному произведению, деленному на произведение их модулей

.

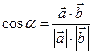Так как скалярное произведение двух векторов, заданных своими координатами, равно сумме попарных произведений одноименных координат, то

.

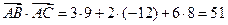Тогда

.

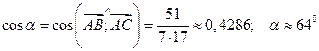3) Уравнение плоскости, проходящей через точку 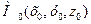перпендикулярно вектору 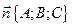, имеет вид

.

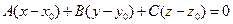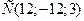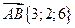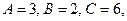
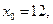
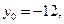
По условию задачи искомая плоскость проходит через точку перпендикулярно вектору . Подставляя 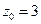, получим:

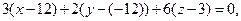
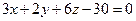– искомое уравнение плоскости.

Задача № 4.Данную систему уравнений решить методом Крамера (с помощью определителей):

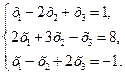
Решение. Вычислим определитель системы Δ по правилу «треугольников»:

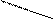
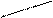
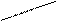
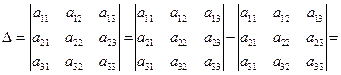(a₁₁ a₂₂ a₃₃ + a₂₁ a₃₂ a₁₃+ a₁₂ a₂₃ a₃₁) – ( a₃₁ a₂₂ a₁₃+ a₃₂ a₂₃ a₁₁+ a₂₁ a₁₂ a₃₃).

Итак,

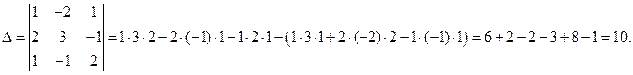
Δ≠0 система имеет единственное решение, которое находим по формулам Крамера:

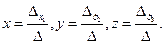
Определители 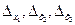получаем заменой соответствующего столбца определителя Δ столбцом свободных членов системы.

Вычислим определители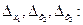

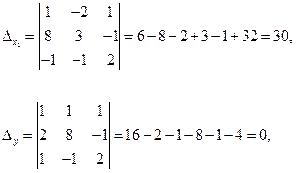
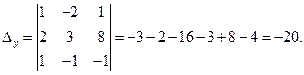
Таким образом,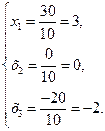

Сделаем проверку, подставив найденное решение в каждое уравнение данной системы:

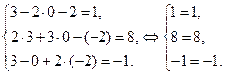– верно.

Ответ: (3;0;-2).

Задача № 5.Вычислить пределы:

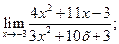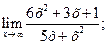а) б) в)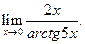

Решение. а) Подстановка предельного значения аргумента х= -3 приводит к неопределенному выражению вида .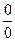

Для устранения этой неопределенности разложим числитель и знаменатель дроби на множители и сократим дробь на множитель . Такое сокращение возможно, так как множитель отличен от нуля при :

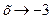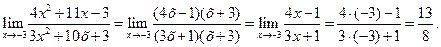
б) При х→∞ числитель и знаменатель дроби 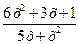стремятся к ∞.

Тогда получаем неопределённость вида 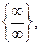которая раскрывается по следующему правилу: предел отношения двух бесконечно больших функций, являющихся многочленами, равен пределу отношения их слагаемых со старшей степенью переменной.

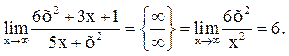
Итак,

в) Для раскрытия неопределённости вида 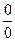, содержащей тригонометрические функции, воспользуемся эквивалентными функциями:

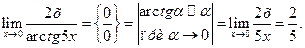
Контрольная работа № 2

Задача № 6. Провести полное исследование функции и построить её график:

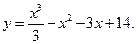
Решение. Проведём исследование функции по следующей схеме:

1) Область определения функции: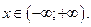

2) Возрастание/убывание, экстремумы функции:

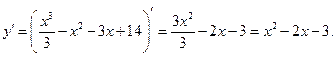
Найдём критические точки функции – точки, в которых y'=0 или не существует:

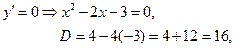
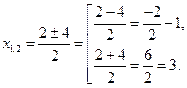
Точек, в которых производная не определена, нет. Отметим полученные точки на числовой прямой:

+ – +

-1 3 х

Определим знак производной на каждом интервале: подставим любую точку из интервала в производную y′=x²-2x-3, тогда знак полученного значения производная сохраняет на всём интервале. Например, y′(-2)=(-2)²-2(-2)-3=5>0,

y′(0)=0²-2∙0-3=-3<0,

y′(4)=4²-2∙4-3=5>0.

Теперь по полученным знакам производной делаем вывод о поведении функции: знак «+» соответствует возрастанию функции, «-» – убыванию. А точки, в которых происходит смена знака, являются точками экстремума функции: х_max= -1, x_min=3. Найдём экстремумы:

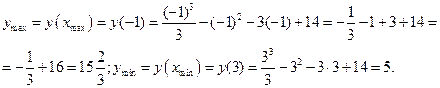
Итак, точка 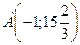– точка максимума, 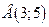– точка минимума.

3) Найдём интервалы выпуклости/вогнутости и точки перегиба графика функции.

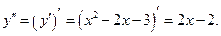
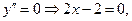
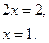
Определим знак второй производной на интервалах (-∞;1) и (1;∞): y"(0)=2∙0-2=-2<0, y"(2)=2∙2-2=2>0. Следовательно, на первом интервале график является выпуклым, на втором – вогнутым, а при х=1 имеет перегиб.

Найдём соответствующее значение функции:

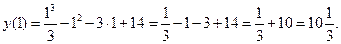
Таким образом, точка 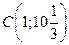– точка перегиба графика функции.

Теперь, пользуясь результатами исследования функции, строим её график (рис. 5).

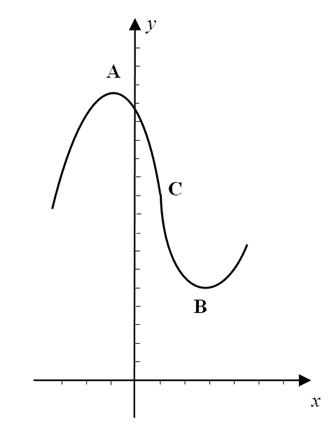Рис. 5

Задача № 7.Найти дифференциал указанной функции.

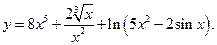
Решение. Преобразуем функцию, применяя свойства степеней:

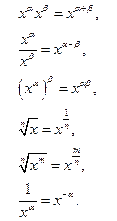
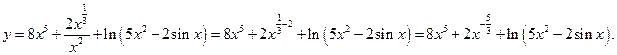
Затем, применяя правила дифференцирования и табличные формулы, получаем:

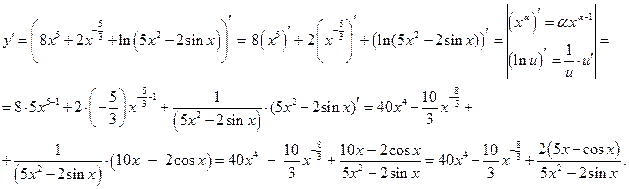
Дифференциал функции равен произведению её производной на дифференциал независимой переменной: 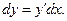Тогда для данной функции:

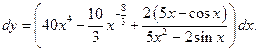
Задача № 8.Исследовать на экстремум функцию .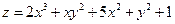

Решение. Находим стационарные точки – точки, в которых частные производные функции равны нулю:

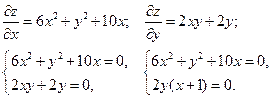
Решение последней системы дает четыре стационарные точки:

.

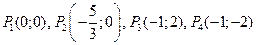Находим частные производные второго порядка:

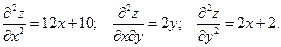
Исследуем каждую стационарную точку.

1) В точке 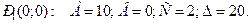Так как 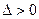и 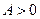, то в этой точке функция имеет минимум.

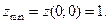
2) В точке 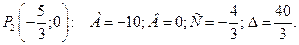Так как 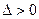и 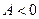, то в этой точке функция имеет максимум.

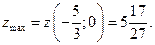
3) В точке 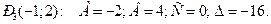Так как 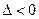, то в этой точке нет экстремума.

4) В точке 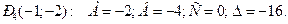Так как 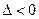, то в этой точке нет экстремума.

Задача № 9.Вычислить площадь фигуры, ограниченной линиями , .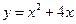

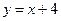Решение. Графиком первой функции является парабола с ветвями вверх, второй функции – прямая.

Найдём координаты вершины параболы:

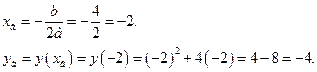
Итак, точка (-2;-4) является вершиной параболы.

Для нахождения точек пересечения данных линий решим систему уравнений:

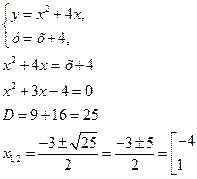
Найдём вторые координаты (ординаты) точек пересечения графиков, подставив найденные значения х в любое из уравнений: y(-4)=-4+4=0, y(1)=1+4=5. Таким образом, парабола и прямая пересекаются в точках (-4;0) и (1;5).

Теперь вершину параболы и точки пересечения используем для построения графиков (рис. 6).

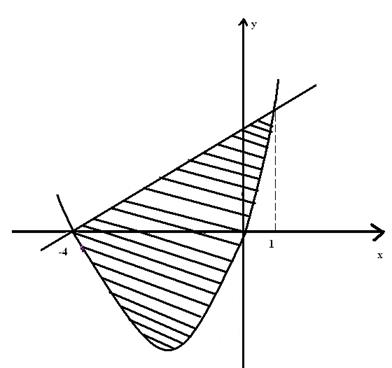
Рис. 6

Площадь фигуры, ограниченной сверху и снизу непрерывными линиями и 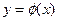, пересекающимися в точках с абсциссами x=a и x=b, определяется по формуле:

.

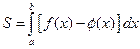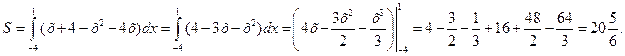
Задача № 10.Найти общее решение дифференциального уравнения 1-го порядка.

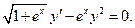
Решение. Это дифференциальное уравнение 1-го порядка с разделяющимися переменными. Находим его решение по стандартной схеме:

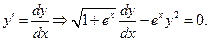
Разделим переменные:

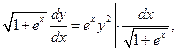
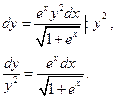
Проинтегрируем обе части уравнения:

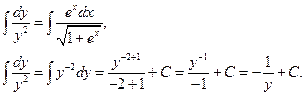
Второй интеграл решим методом замены переменной:

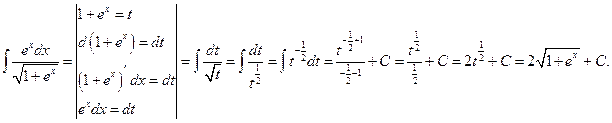
Теперь приравняем результаты, причём произвольную постоянную С запишем только в правой части:

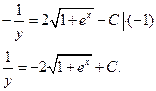
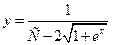–общее решение.

Задача № 11.Найти частное решение дифференциального уравнения 2-го порядка, удовлетворяющее указанным начальным условиям.

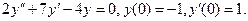
Решение. Это линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами. Общее решение уравнения составляется в зависимости от корней характеристического уравнения:

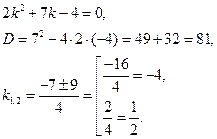
Если корни характеристического уравнения действительны и различны, то общее решение имеет вид: 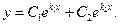В нашем случае 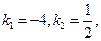значит,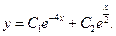

Теперь из общего решения уравнения выделим частное решение, удовлетворяющее заданным начальным условиям.

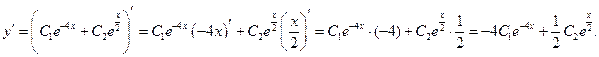
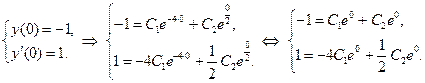
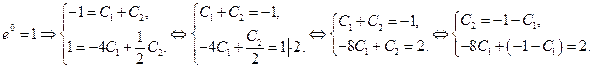
Итак,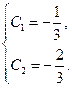

Подставим найденные значения констант в общее решение. Тогда 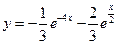– частное решение уравнения.

Задача 12.Дан степенной ряд 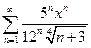. Написать первые три члена ряда, найти интервал сходимости ряда и исследовать его сходимость на концах интервала.

Решение. 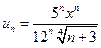– общий член ряда. Подставив в эту формулу вместо n значения 1, 2, 3, …, можно найти любой член ряда:

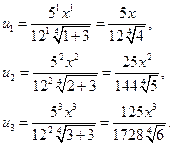
Степенной ряд в общем виде записывается следующим образом: 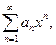где a_n – формула числовых коэффициентов. Для данного ряда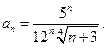

Областью сходимости степенного ряда является интервал (-R;R), где 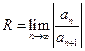– радиус сходимости. Вычислим его:

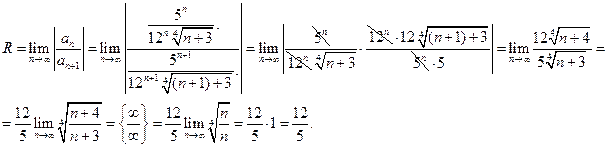
Итак, ряд является сходящимся (абсолютно) при всех х, принадлежащих интервалу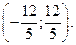

Теперь проверим сходимость ряда на концах этого интервала.

Пусть 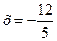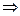получаем ряд: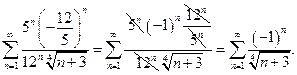

Это числовой знакочередующийся ряд, исследуем его по признаку Лейбница:

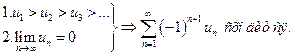
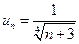
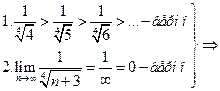ряд сходится, значит, 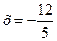– точка сходимости.

При 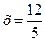исходный ряд принимает вид: 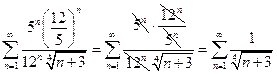– числовой знакоположительный ряд. Исследуем его сходимость при помощи интегрального признака сходимости Коши. Рассмотрим несобственный интеграл: 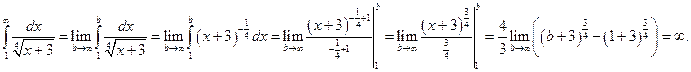Так как несобственный интеграл расходится, то расходится и исследуемый ряд. Значит, 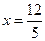– точка расходимости.

Таким образом, данный степенной ряд является сходящимся при