Основные уравнения строительной механики

Математическая сторона основной задачи строительной механики основана на зависимостях, полученных в сопромате. Напомним их на примере напряженно-деформированного состояния элемента рамы, для которого – в отличие от балки – поперечный изгиб сопровождается дополнительным растяжением или сжатием.

Пусть такой элемент длиной dx расположен в локальной системе координат Oxy, где ось Ox направлена по оси стержня, и загружен распределенной нагрузкой интенсивностью q_x и q_y вдоль Ox и Oy соответственно (рис. 1.20).

Напряженно-деформированное состояние стержня определяется девятью компонентами:

– внутренними усилиями (M, Q, N,);

– перемещениями (u, v, q);

– деформациями (κ, g, e).

Уравнения для определения этих функций можно разделить на три группы.

Статические уравнения – связывают внутренние усилия (рис. 1.20, б) с заданной нагрузкой:

dN/dx = – q_x; ü

dQ/dx = q_y; ý (1.10)

dM/dx = Q . þ

Геометрические уравнения – выражают деформации через перемещения, показанные на рис. 1.20, в, г:

κ = dq/dx; ü

g = q - dv/dx; ý (1.11)

e = du/dx. þ

Физические уравнения – представляют собой зависимости между внутренними усилиями и деформациями:

κ = M/EJ; ü

g = mQ/GF; ý (1.12)

e = N/EF; þ

где E – модуль Юнга;

G – модуль сдвига;

F – площадь поперечного сечения стержня;

J – момент его инерции;

m – коэффициент, учитывающий неравномерность распределения касательных напряжений в поперечном сечении стержня.

Q > 0

γ>0

Q+dQ

M > 0

N+dN

qx > 0

qy > 0

u>0

θ>0

N > 0

M+dM

θ+dθ > 0

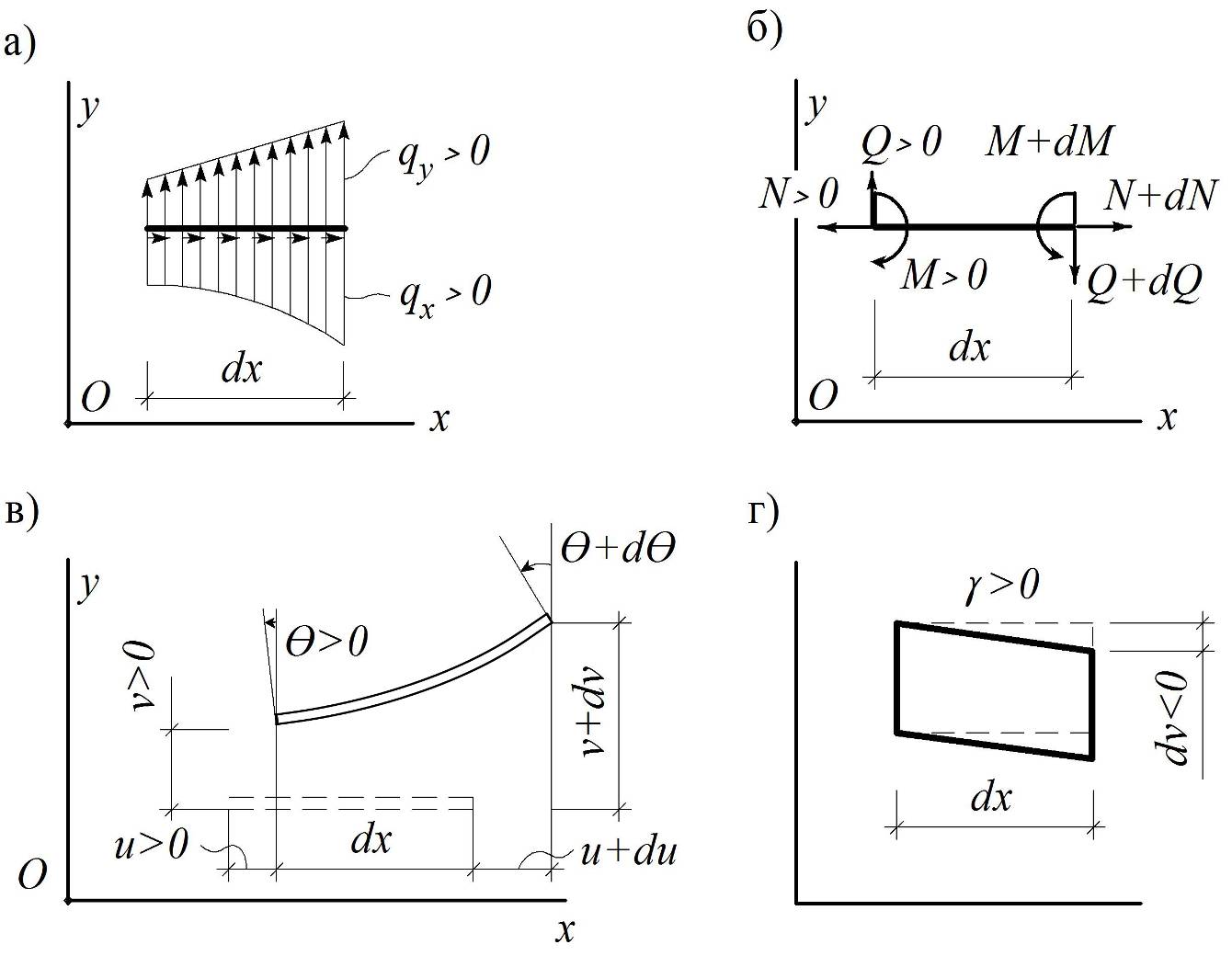
Рис.1.20

Отметим, что выражения EJ и EF в (1.12) называются жесткостями стержня при изгибе и растяжении (сжатии) соответственно.

При решении системы уравнений (1.10) – (1.12) возможны два варианта:

1) внутренние усилия M, Q, N удается найти из системы уравнений (1.10), не обращаясь к остальным уравнениям – это СОС;

2) внутренние усилия можно найти только путем совместного решения всех девяти уравнений – это СНС.

В последнем случае при решении этих уравнений возможны два подхода:

– в качестве основных неизвестных выбирают усилия M, Q, N, выражая все остальные через них – это решение в форме метода сил;

– в качестве основных неизвестных выбирают перемещения u, v, q – это решение в форме метода перемещений.

Системы, описываемые линейными уравнениями (1.10) - (1.12), называются линейно-деформируемыми. Для них справедлив принцип суперпозиции, в соответствии с которым:

внутренние усилия, перемещения и деформации от заданной нагрузки (или иного воздействия) можно найти как сумму соответствующих величин от каждой нагрузки в отдельности.

Примечания

1. Первое из статических уравнений (1.10) получается из условия равновесия рассматриваемого элемента рамы. Полагая в его пределах q_x = const, и составляя уравнение SX = 0, получим:

– N + q_x×dx + (N +dN) = 0,

откуда и следует искомая зависимость. Два других уравнения из (1.10) – это дифференциальные зависимости Журавского.

2. Первое из физических уравнений (1.12) представляет собой дифференциальное уравнение изогнутой оси балки:

κ = dq/dx = d ²v/dx ² = M /EJ.

Второе уравнение в предпосылке равномерного распределения касательных напряжений в поперечном сечении стержня (m =1) выражает закон Гука при сдвиге:

t = Q/F = Gg.

При этом мы не уточняем смысл коэффициента m по причине, которая будет указана в § 3.5. Последнее из физических уравнений (1.12) – это закон Гука при ЦРС:

s = N/F = E×e.

3. В дальнейшем мы будет по-прежнему применять обозначение Oxy для глобальной системы координат, связанной с конструкцией в целом.