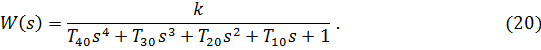Составление передаточной функции
Конструкция и принцип действия гидроусилителя
Согласно представленному заданию в качестве объекта исследования представлен гидроусилитель с устройством «струйная трубка» и подвижным выходным звеном в виде корпуса гидроцилиндра. Рассмотрим более подробно конструкцию данного устройства (рис. 1).

Рис. 1. Гидроусилитель с устройством «СТРУЙНАЯ ТРУБКА»
Чувствительным элементом данного следящего устройства является струйная трубка 1. Плита 2 выполнена заодно с корпусом гидроцилиндра и может перемещаться в направляющих 3. Поршень 4 закреплен неподвижно.
Принцип действия
Под действием изменяющегося усилия P и деформации линейной пружины П струйная трубка поворачивается на малый угол φ, например, по часовой стрелке возникает перепад давления p=p1-p2>0. Плита 2, а соответственно, и корпус гидроцилиндра перемещаются влево. Если в процессе движения сила P сохраняет свое постоянное значение и внешняя активная нагрузка Pa=0, то со временем плита 2 займет положением, при котором имеет место приближенное равенство δ=y.
В замкнутом усилителе сигнал, приводящий к изменению усилия P, формируется как результат замыкания управляющего воздействия на ГУ и воздействия, поступающего по каналу ГОС.
На рис. 1 также введены следующие обозначения:
· a, b – плечо приложенной cилы P и длина струйной трубки соответственно;
· φ и δ – угол поворота и смещение среза сопла трубки;
· p1 и p2 – давления в полостях гидроцилиндра;
· Q1 и Q2 – расходы, втекающие и вытекающие из полостей гидроцилиндра;
· F – эффективная площадь поршня гидроцилиндра.
Составление передаточной функции
Запишем уравнение струйной трубки. Вращающий момент струйной трубки от усилия P уравновешивается инерционным моментом, моментом от сил трения в опорах и моментом от усилия, развиваемого пружиной П. Следовательно
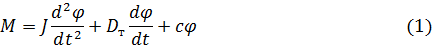
где: J – момент инерции трубки;
Dт – коэффициент демпфирования;
с – приведенный коэффициент жесткости пружины П.
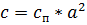 (2)
(2)
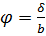 (3)
(3)
где: 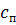 – жесткость пружины;
– жесткость пружины;
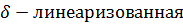 длина дуги, описываемая концом трубки.
длина дуги, описываемая концом трубки.
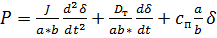 (4)
(4)
Перепишем уравнение (4) в виде приращений, учитывая, что для малых приращений справедливо
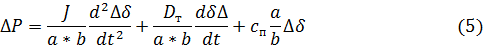
Запишем уравнение поршня гидроцилиндра с учетом действия на него и инерционной составляющей и с учетом сил, действующих со стороны пружин
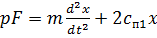 (6)
(6)
Перепад давления является функцией смещения конца трубки от среднего положения и расхода 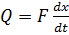 , поступающего в цилиндр, то есть
, поступающего в цилиндр, то есть 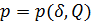 . Линеаризация в окрестности точки δ=Q=0 дает
. Линеаризация в окрестности точки δ=Q=0 дает
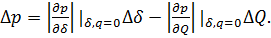 (7)
(7)
Линеаризованное уравнение движения поршня гидроцилиндра запишется в виде
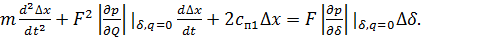 (8)
(8)
Исключая из уравнений (5) и (8) переменную 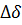 и опуская символ
и опуская символ  , окончательно получим
, окончательно получим
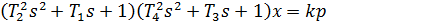 (9)
(9)
где: T1 – T4 – постоянные времени,
k – коэффициент усиления.


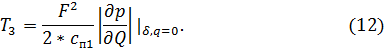

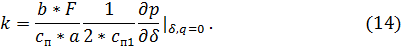
Перемножим между собой два получившихся трехчлена (9) и в результате упрощения получим
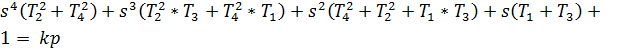 (15)
(15)
Введем обозначения
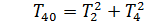 (16)
(16)
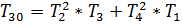 (17)
(17)
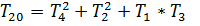 (18)
(18)
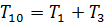 . (19)
. (19)
Таким образом получена передаточная функция исследуемой системы автоматического регулирования