Экспериментальное определение констант критериального уравнения

При проведении опытов измеряют и определяют размерные величины, содержащиеся во всех критериях подобия. По результатам опытов вычисляют значения критериев. Затем составляют таблицы, в которые соответственно значениям критерия вписывают значения определяющих критериев и т.д. Этой операцией завершается подготовительный этап обработки опытов.

Для обобщения табличных данных в виде степенной зависимости:

используется логарифмическая система координат. Подбором показателей степени и т.д. добиваются такого расположения опытных точек на графике, чтобы через них можно было провести прямую линию. Уравнение прямой линии дает искомую зависимость между критериями.

Покажем, как на практике определить константы критериального уравнения:

.

В логарифмических координатах это уравнение прямой линии:

.

Нанося опытные точки на график (рис. 4), проводят через них прямую линию, наклон которой определяет значение постоянной .

Рис. 4. Обработка опытных данных

Остается найти постоянную 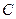. Для любой точки прямой на графике . Поэтому значение 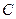находят по любой паре соответствующих значений и , отсчитанных на прямой линии графика. Для надежности значения 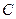определяют по нескольким точкам прямой и в конечную формулу подставляют среднее значение:

При большем числе критериев определение констант уравнения несколько усложняется и проводится по методике, описанной в книге [33[VK2] ].

В логарифмических координатах не всегда удается расположить опытные точки вдоль прямой линии. Это случается, когда наблюдаемая зависимость не описывается степенным уравнением и надо искать функцию другого вида.

Третья теорема подобия

Новые типы бытовых машин и приборов разрабатываются по результатам, полученным на моделях и экспериментальных установках. Процессы в экспери-ментальных установках должны быть подобны тем, которые будут протекать в промышленном образце.

Две первые теоремы распространяются на явления, обладающие подобием. Третья теорема подобия М.В. Кирпичева и А.А. Гухмана (1931 г.) определяет необходимые и достаточные условия, при которых явления можно считать подобными: подобны те явления, которые описываются одной и той же системой дифференциальных уравнений и имеют подобные условия однозначности.

Требование условий однозначности при критериальном обобщении имеет тот же смысл, что и установление единственности (однозначности) аналитического решения физических дифференциальных уравнений.

Дифференциальное уравнение описывает широкий круг явлений данного класса, основой которых является общий закон физики (например, класс явлений распространения тепла). Однако такое общее уравнение не отражает индивидуальных признаков частного явления (например, прогрева ткани утюгом). Поэтому исходному уравнению удовлетворяет множество решений. Специалиста обычно интересует конкретное явление данного класса, наблюдаемое в условиях работы определенной машины или прибора. Поэтому из множества возможных решений исходного уравнения (или системы уравнений) надо выбрать одно решение, соответствующее индивидуальному явлению. Для этого в условия задачи вводят дополнительные условия однозначности (краевые условия), не содержащиеся в исходной системе уравнений и ограничивающие решение единственным конкретным случаем. Условия однозначности включают следующие необходимые данные:

1) сведения о геометрических свойствах системы (конфигурация и размеры рабочего объема аппарата);

2) данные о физических свойствах продуктов и материалов (теплопроводность, теплоемкость стенок аппарата, вязкость, плотность рабочих сред и др.);

3) данные о состоянии системы на ее границах (граничные или пространственные краевые условия) и о взаимодействии с окружающей средой (интенсивность теплообмена или массообмена, распределение температур или концентраций на поверхности и др.);

4) данные о состоянии системы в начальный и конечный моменты времени процесса (временные условия).

Исходная система физических уравнений совместно с условиями однозначности определяет конкретные явления данного класса. Решение такой системы в виде формулы не всегда может быть получено из-за чрезмерной сложности ее вывода. В этом случае прибегают к методу обобщенных переменных, т.е. к теории подобия.

Очевидно, критерии подобия следует выводить не только из основного физического уравнения процесса, но и из уравнений, составляющих условия однозначности. Результатом подобия условий однозначности будет одинаковый вид функций и совпадение значений искомого критерия для двух и ряда подобных процессов.