Законы сохранения для плотностей числа частиц, импульса и энергии

Линейный закон представляет собой обобщение известных эмпирических фактов, сформулированных в виде законов:

а) уравнение диффузии, закон Фика- ;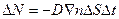

б) уравнение теплопроводности, уравнение Фурье- ;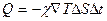

в) Закон Ома 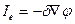, I_e-поток заряда,

где DN, DQ-соответственно количество частиц и теплоты, проходящих через площадь DS за время Dt, Ñn=Dn/Dx-градиент плотности числа частиц, ÑТ=DТ/Dх- градиент температуры, D- коэффициент диффузии, c-коэффициент теплопроводности, Ñj-градиент потенциала.

Процессы переноса, в которых градиенты данного свойства вызывает поток этого же физического свойства называют прямыми процессами переноса. Существуют непрямые (перекрёстные) процессы переноса, в которых градиент одного физического свойства вызывает поток другого физического свойства. Пример - термодиффузионные явления. Если имеет место два градиента: концентрации n и температуры T, то в такой среде возникают потоки частиц и тепла

.

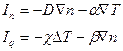Процесс возникновения потока частиц под действием градиента температуры носит название эффекта Дюфура, а процесс возникновения потока тепла под действием градиента концентрации называется эффектом Соре.

Введём в рассмотрение термодинамические силы

,

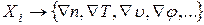связанные с градиентами различных физических величин (плотности, температуры, скорости, потенциала) и также вызываемые этими силами потоки

.

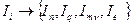Линейный закон термодинамики необратимых процессов утверждает: каждый поток представляет собой линейную комбинацию термодинамических сил

,

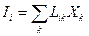L_ik - кинетический коэффициент

Рассмотрим в формуле (2.2) увеличение энтропии при изменении локальных макроскопических параметров A в адиабатных условиях как термодинамические силы X_i необратимых процессов, а величину 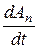как термодинамические потоки I_i. В результате получим обобщённое выражение для локального производства энтропии

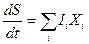. (2.3)

Соотношение (2.3) основная формула макроскопической термодинамики необратимых процессов. Линейный закон справедлив только при сравнительно небольших отклонениях системы от положения равновесия. В линейной термодинамике необратимых процессов выделяются три принципа:

1.Соотношение взаимности Онзагера, утверждающее, что кинетические коэффициенты сопряженных процессов равны, т.е. L_ik=L_ki.Существует принцип Кюри: линейный закон для каждого потока должен связывать потоки и термодинамические силы одной и той же тензорной размерности. В связи с этим необходимо различать векторные потоки, связанные с переносом энергии и вещества (градиенты температур, химического потенциала и соответствующие потоки тепла, частиц); тензорные силы и потоки, описывающие перенос импульса, в терминах сдвиговой вязкости (градиент скорости и тензор потока импульса); скалярные силы и потоки – давление и дивергенция скорости.

Принцип Кюри позволяет установить факты, согласно которым, например, в результате химической реакции (скалярный процесс) не может возникнуть диффузия (векторный процесс).

2. Второй принцип линейно необратимых систем характеризует их стационарное, не зависимое от времени состояние. Возникает вопрос о специфической особенности стационарных (установившихся) необратимых процессов, отличающих их от нестационарных (неустановившихся, переходных) процессов. Вопрос заключается об обнаружении физической величины, которая при стационарном процессе имела бы экстремальное значение, подобно тому, как равновесные состояния характеризуются максимальной энтропией. В работах И. Пригожина по неравновесной термодинамике это положение сформулировано как принцип минимума производства энтропии в стационарном необратимом процессе

, .

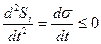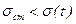Здесь 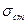- производство энтропии в стационарном состоянии, 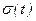- производство энтропии в момент установления стационарного состояния.

Производство энтропии необратимых процессов обусловлено диссипацией энергии – переходом части энергии упорядоченного движения в энергию неупорядоченного движения (в конечном итоге в теплоту).

Третий принцип линейной термодинамики – принцип текущего равновесия. Он показывает, что стационарные состояния открытых неравновесных систем обладают свойствами устойчивости. При незначительном внешнем воздействии на систему в стационарном состоянии в ней возникают внутренние потоки, ослабляющие результаты этого воздействия и система стремиться вернуться в стационарное состояние.

Для поддержания устойчивого стационарного состояния должен происходить приток отрицательной энтропии в объёме системы, компенсирующий производство энтропии в ней, а так же приток вещества, компенсирующего изменения, вызванные химическими реакциями.

Таким образом, принципиальное различие между термодинамическим равновесием и текущим равновесием связано наличием конечного производства энтропии. Состояние текущего равновесия однородно в пространстве, упорядочение и образование новых структур в области линейных необратимых процессов невозможны.

Нелинейная термодинамика

Нелинейная термодинамика имеет дело с открытыми системами, далёкими от равновесия, когда связь между термодинамическими потоками и силами перестаёт быть линейной, а соотношение Онзагера не выполняется. Открытые системы в отличие от замкнутых или изолированных систем могут обмениваться с окружающими телами как энергией и веществом, так и информацией. Открытые системы являются макроскопическими, то есть состоят из очень большого числа структурных объектов, принимаемых за элементарные. Установлено, что в нелинейной области неравновестности открытые системы способны развиваться, то есть спонтанно образовывать упорядоченные структуры, само- организовываться. Отдельные примеры подобных процессов были известны. Это возникновение турбулентности, вихрей, образование ячеистой структуры в неоднородно нагретом горизонтальном слое жидкости. Общим во всех явлениях образования упорядоченных структур при необратимых процессах в сильно неравновесных, открытых системах, является совместное кооперативное движение больших групп молекул или других элементарных структурных единиц системы. Немецкий учёный Хакен предложил для таких процессов самоорганизации общий термин «синергетика» - в переводе с греческого означает совместное, кооперативное действие.

Физическая природа синергетики состоит в том, что нелинейной области вдали от равновесного состояния система теряет устойчивость и малые флуктуации приводят к новому режиму – совокупному движению многих частиц.

Принцип синергетики

В открытых системах, вдали от равновесия, в нелинейной области реализуется принцип «неравновесность» - источник упорядоченности. Энтропия, служащая мерой беспорядка, может уменьшиться в открытых системах с течением времени, благодаря связи системы с окружающей системой. Открытая система подводимую от внешнего источника энергию диссипирует в термостат, при этом внутрисистемное производство энергии увеличивается, т.е. 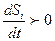. Однако если система экспортирует энтропию во внешнюю среду, т.е. потоковое слагаемое энтропии отрицательное.

.

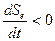Если

,

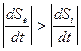то полная энтропия открытой системы уменьшается. Такая система становиться активной, т. е. способной к самоорганизации. В активной среде возникает устойчивая флуктуация, которая становиться источником образования новой структуры.

Структуры, возникающие в результате самоорганизации открытых нелинейных систем, Пригожин назвал диссипативными. Эффект образования диссипативных структур классифицируется как кинетический фазовый переход. В отличие от классических термодинамических фазовых переходов (плавление, кристаллизация), у которых радиус корреляции имеет атомные масштабы, в случае кинетических фазовых переходов радиус корреляции сложной системы достигает макромасштабы.

Схема термодинамической ветви развития открытых систем приведена на рисунке 1. Точки 1,2,3 пороговые значения управляющего параметра, при достижении которых открытая система теряет динамическую устойчивость (состояния A,B,C)

Состояния неустойчивости A,B,C называются бифуркациями. В точке бифуркации система становиться весьма чувствительной к слабым сигналам, от которых зависит вариант образования диссипативных структур, то есть дальнейший путь развития системы. Между точками бифуркаций в системе выполняются детерминистические законы, но в окрестности точек бифуркации важную роль играют флуктуации и вероятностные закономерности. Нелинейная термодинамика коренным образом изменяет статус II начала термодинамики. Этот закон определяет не только разрушение структур при необратимых процесса вблизи равновесного состояния, но и возникновения структур при необратимых процессах, вдали от равновесия открытой системы. Отражая необратимость всех реальных процессов, второе начало отражает закон развития материи.