Влияние стационарного электрического поля на оптические свойства кристаллов

Рассмотренная в предыдущем параграфе оптическая анизотропия обусловлена лишь физическими свойствами среды, ее структурой. Та­кая анизотропия не связана с воздействием внешних полей, поэтому она называется естественной. Внешние поля могут менять структуру, а зна­чит, и симметрийные свойства среды. В силу принципа Кюри кристалл, находящийся под внешним воздействием, сохраняет лишь элементы симметрии, общие с элементами симметрии воздействия. Так что, на­пример, изотропная среда может стать оптически анизотропной.

Эффекты, состоящие в индуцировании оптической анизотропии электрическим полем, называются электрооптическими. Они наблюда­ются в неподвижных материалах, помещенных в сильное стационарное электрическое поле, когда по такому фоновому состоянию (отличаю­щемуся от естественного в отсутствие поля) пропускается электромаг­нитная волна (свет). В узком смысле электрооптическим эффектом на­зывается изменение показателя преломления света в кристалле, вызванное стационарным внешним электрическим полем. Важнейшими электрооптическими эффектами являются эффекты Поккельса (линей­ный) и Керра (квадратичный). В этом приближении зависимость пока­зателя преломления п от стационарного внешнего поля 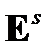имеет вид:

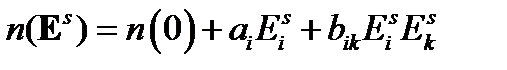(57)

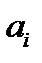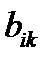где и - величины, определяемые константами Поккельса и Кер­ра, описывающими линейный и квадратичный эффекты соответственно.

Характер эффекта зависит от симметрии исходного (естественного) кристалла. Линейный электрооптический эффект возможен только в кристаллах, группа симметрии которых не содержит преобразования инверсии (нецентросимметричные кристаллы). В центросимметричных кристаллах, а также в изотропных средах возможен лишь квадратичный эффект. Квадратичный эффект может наблюдаться и на кристаллах, проявляющих линейный электрооптический эффект. В большинстве случаев он дает лишь малые добавки к основному линейному эффекту.

Если же направление поля 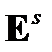в кристалле таково, что соответ­ствующие ему константы 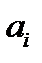(57) равны нулю, квадратичный эффект становится определяющим.

Учет последующих членов в разложении (57) приводит к электро­оптическим эффектам более высокого порядка. Ниже рассматривается только линейный электрооптический эффект - эффект Поккельса.

Следует отметить, что величина электрооптического эффекта зави­сит также и от механического состояния кристалла. Так, если кристалл свободен, то вследствие обратного пьезоэлектрического эффекта стати­ческое электрическое поле будет вызывать деформации, которые в свою очередь вследствие пьезооптического эффекта будут приводить к изме­нению показателя преломления.

Электрооптический эффект, возникающий в кристалле с запре­щенными деформациями (механически зажат), называется первичным, а эффект, обусловленный деформациями кристалла, - вторичным.

Эффект, наблюдаемый в свободном кристалле, равен сумме первичного и вторичного. В данной работе исследуется лишь первичный эффект Поккельса.

Существование электрооптических эффектов в материальной среде свидетельствует о том, что уравнения для электромагнитного поля в этой материальной среде в отличие от подобных уравнений в вакууме нелинейны. Анализ электрооптических эффектов, хотя и основанный на нелинейных уравнениях (для которых все решения, кроме самых про­стых, трудно получить), можно сделать простым и прозрачным, если предположить, что нестационарная часть решения - световая волна - имеет столь малую интенсивность, что описывающие ее векторы можно

считать бесконечно малыми в сравнении с E^s . Иными словами, поле волны Е₀(39) является малым возмущением по отношению к смещаю­щему полю E^s .

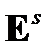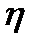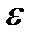В этом довольно общем подходе к анализу электрооптического эффекта предполагается, что электрическая индукция D является функцией напряженности стационарного внешнего поля и линей­ным функционалом возмущающего нестационарного поля световой волны. Следствием этого является зависимость материальных характе­ристик и от 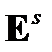. В рассматриваемом случае эффекта Поккельса для тензора 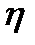имеем:

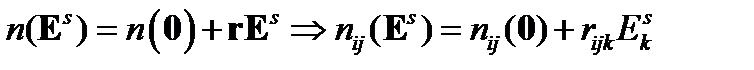(58)

где постоянные Поккельса 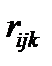- компоненты тензора 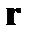(третьего ранга) электрооптических коэффициентов.

Для удобства практического использования коэффициентов 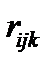два первых тензорных индекса i, j заменяются одним матричным 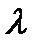. Схема замены 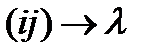индексов выглядит следующим образом:

i
j

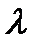В результате замены 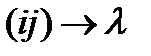индексов постоянные Поккельса мо­гут быть представлены матрицей 6x3. Симметрийные свойства кри­сталла определяют элементы матрицы 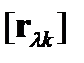, равные нулю, а также соот­ношения между ненулевыми коэффициентами 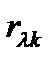, вследствие которых уменьшается число независимых элементов матрицы .

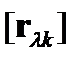Найдем индуцированное полем 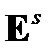изменение 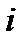-го главного пока­зателя преломления 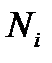(50). С учетом малости второго слагаемого в (58), запишем:

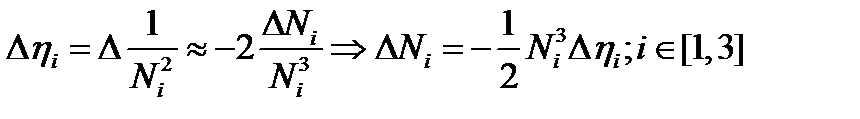(59)

С той же точностью изменение 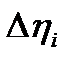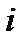-го главного значения тензора 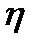согласно (58) равно

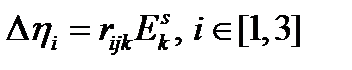(60)

Подставив (60) в (59), получим:

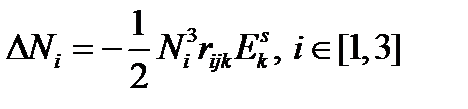(61)

Величина 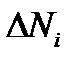- это индуцированное полем изменение 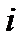-й полуоси эллипсоида Пуансо (оптической индикатрисы). Можно показать, что недиагональные компоненты тензора 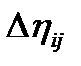описывают вращение эллипсоида (50), следствием которого является изменение поляризации волн. Численные значения 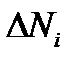определяются материальными харак­теристиками кристалла. Электрооптический эффект считается значи­тельным, если 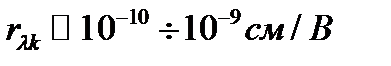. Поэтому при обычных внеш­них полях ~ 10⁴ В/см линейное изменение (61) показателя

преломления составляет 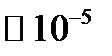. Это означает, что существенные из­менения оптической длины вследствие эффекта Поккельса могут быть получены только в тех случаях, когда длина кристалла в на­правлении распространения света ~ в 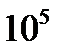раз превышает длину вол­ны света.