Обыкновенные дроби и дробные выражения
МИНИСТЕРСТВО ОБРАЗОВАНИЯ НИЖЕГОРОДСКОЙ ОБЛАСТИ
Государственное бюджетное образовательное учреждение
Среднего профессионального образования
«НИЖЕГОРОДСКИЙ КОЛЛЕДЖ МАЛОГО БИЗНЕСА»
Методические указания для студентов по подготовке к экзамену по учебной дисциплине «Математика»
Для студентов 1 курса СПО
Учебно-методическое пособие
Нижний Новгород
Содержание:
Введение 3
Обыкновенные дроби и дробные выражения 5
Контрольные вопросы и задания для самостоятельного решения по разделу 1 11
Проценты 12
Контрольные вопросы и задания для самостоятельного решения по разделу 2 17
Степени и корни 19
Контрольные вопросы и задания для самостоятельного решения по разделу 3 23
Уравнения и методы их решения 24
Контрольные вопросы и задания для самостоятельного решения по разделу 4 28
Логарифмы 30
Контрольные вопросы и задания для самостоятельного решения по разделу 5 38
Простейшие задачи по теории вероятностей 40
Контрольные вопросы и задания для самостоятельного решения по разделу 6 43
Простейшие тригонометрические уравнения 44
Контрольные вопросы и задания для самостоятельного решения по разделу 7 51
Производные элементарных функций 53
Контрольные вопросы и задания для самостоятельного решения по разделу 8 60
Площадь криволинейной трапеции 62
Контрольные вопросы и задания для самостоятельного решения 68
литература и интернет ресурсы 70
Введение
Реформа современного образования может состояться лишь при условии создания таких компьютерных пакетов (электронных учебников, пособий, тренажеров, тестеров и проч.), наличие которых обеспечит одну и ту же компьютерную среду в специализированной аудитории на практических занятиях, в компьютерном классе учебного заведения или общежитии, оборудованном для самостоятельной работы учащихся, а также дома на персональном компьютере.
Электронный учебник (или электронное пособие) не может и не должен заменять книгу! Так же как просмотр фильма не заменяет чтения книги, по которой он был поставлен, так и наличие электронного пособия не только не должно заменять чтения и изучения обычного учебника, а напротив, побуждать студента взяться за книгу.
Как готовиться к экзамену по математике?
70% ошибок на экзаменах – по темам из начальной школы! Это дроби, отрицательные числа, элементарные преобразования выражений и все такое же простенькое. Высокий полет математической мысли заканчивается ошибками на уровне пятого класса. Чтобы подготовиться к экзамену по математике, первым делом нужно ликвидировать пробелы из прошлого. А так же необходимо освоить математические определения и термины! Студенты должны понимать, к примеру, что такое знаменатель, дискриминант, или функция на простом, даже примитивном уровне. Что это такое, зачем это нужно и как с этим обращаться. И, конечно, нужно решать. Нужно пытаться решать, пробовать. Все когда-то не умели. Но кто пытался и пробовал, пусть и неправильно, с ошибками - тот сейчас умеет решать. А кто не пробовал, типа всё равно не получается... - тот так и не научился.
Вот вам три составляющие ответа на вопрос "Как готовиться к экзамену по математике?»:
- ликвидировать пробелы,
- освоить термины на понятном уровне,
- осмысленно решать задания.
Математика школьного курса не решает сложные примеры. Вся мощь математики направлена на упрощение сложных выражений. Именно для этого нужны правила и формулы различных преобразований. Они позволяют записывать исходное выражение в другом, удобном виде, не меняя его сущности.
Например:
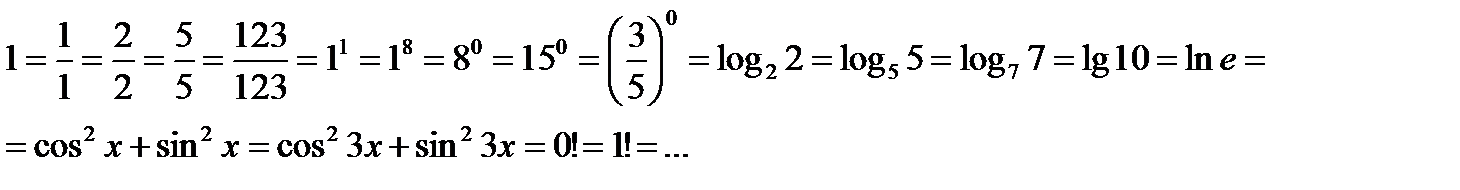
Это всё одно и то же число 1!
Только записанное в самых разных видах. Какой вид выбрать зависит от задания.
Практически любое решение начинается с преобразования исходного выражения. С помощью правил и формул. Формулы нужно знать!
Преобразования выражений – вещь, поначалу, хлопотная. На стартовом этапе нужно проверять, где можно, правильность преобразования обратным преобразованием. Т.е. разложили на множители – перемножьте обратно и приведите подобные. Нашли корни уравнения – подставьте в исходное выражение. Посмотрите, что получилось. И так далее.
Как пользоваться ЭП (электронным пособием)?
ЭП состоит из нескольких разделов, каждый из которых имеет две части:
- основные теоретические сведения с примерами решения заданий
- контрольные вопросы и задания для самостоятельного решения
С помощью гиперссылок (знак ) можно вернуться к оглавлению, чтобы перейти другому разделу, или к какой либо части текущего раздела. Все темы ЭП являются повторение пройденного материала и иллюстрированы вставками из презентаций, показанных на занятиях в течение всего первого курса. Все примеры подобны заданиям экзаменационной работы.
Обыкновенные дроби и дробные выражения
Итак, какие бывают дроби?
Дроби бывают трёх видов. Обыкновенные, десятичные и смешанные числа (содержащие целую и дробную части).
Десятичные дроби и смешанные числа всегда можно перевести в обыкновенные дроби. Обратный перевод не всегда возможен. Смешанные числа практически не используются в старших классах. Для того, чтобы с ними работать, их всяко надо переводить в обыкновенные («неправильные») дроби. Выбор вида дробей для работы с заданием зависит от этого самого задания. При наличии разных видов дробей в одном задании, самое надёжное - перейти к обыкновенным дробям.
Всё многообразие преобразований дробей обеспечивается одним-единственным свойством! Оно так и называется, основное свойство дроби: если числитель и знаменатель дроби умножить (разделить) на одно и то же число, дробь не изменится.
Кстати, если в дроби стоят всякие логарифмы, синусы и прочие буковки, это ничего не меняет. В том смысле, что все действия с дробными выражениями ничем не отличаются от действий с обыкновенными дробями!
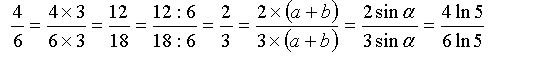
Любое целое число можно записать в виде дроби. В числителе - само число, в знаменателе - единица. С буквами - то же самое.
Иногда вместо горизонтальной чёрточки ставят наклонную черту: 1/2, 3/4, 19/5, ну, и так далее. Чёрточка, что горизонтальная, что наклонная, означает деление верхнего числа (числителя) на нижнее (знаменатель).
Иногда в примерах возникает такой казус как «трёхэтажная дробь»:

Т.е. всё зависит от того какую черту считать главной.
Десятичные дроби
С десятичными дробями всё просто. Как слышится, так и пишется!
Например:
Ноль целых, двадцать пять сотых (0,25) так и пишем: 25/100.
Сокращаем (делим числитель и знаменатель на 25),
получаем обычную дробь: 1/4.
Любую десятичную дробь можно превратить в обыкновенную.
Но не каждая обыкновенная дробь переводится в десятичную!


Для работы со смешанными числами их нужно перевести в обыкновенные (неправильные) дроби. Как это сделать? Надо знаменатель дробной части умножить на целую часть и прибавить числитель дробной части. Это будет числитель обычной дроби. А знаменатель? Знаменатель останется тем же самым. Звучит сложно, но на деле всё элементарно.
Например:
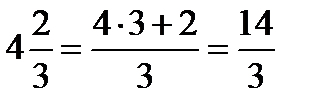
Действия с обыкновенными дробями:
Сложение и вычитание дробей
Сложить (отнять) дроби с одинаковыми знаменателями просто: при сложении (вычитании) знаменатель не меняется. Числители складываются (вычитаются) и дают числитель результата. Например:
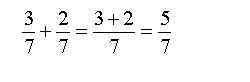
Или:
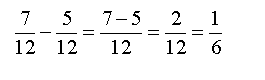
В общем виде:
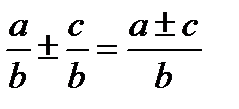
А если знаменатели разные? Тогда, используя основное свойство дроби делаем знаменатели одинаковыми! Это называется «приведём к общему знаменателю».
Например:
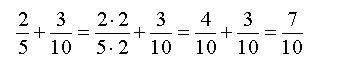
или
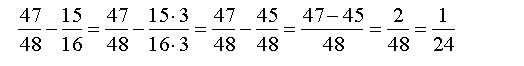
или
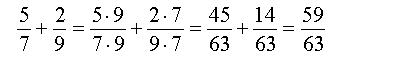
То же самое происходит если надо сложить два дробных выражения:
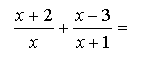
Надо сделать знаменатели одинаковыми. Так и записываем, черту дроби, сверху пустое место оставим, потом допишем, а снизу пишем произведение знаменателей, чтобы не забыть:
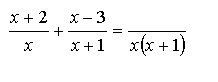
И, конечно, ничего в правой части не перемножаем, скобки не открываем! А теперь, глядя на общий знаменатель правой части, соображаем: чтобы в первой дроби получился знаменатель х(х+1), надо числитель и знаменатель этой дроби умножить на (х+1). А во второй дроби - на х. Получится вот что:
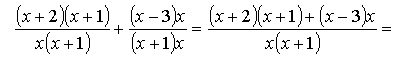
Обратите внимание! Здесь появились скобки! Скобки появляются потому, что мы умножаем весь числитель и весь знаменатель! А не их отдельные кусочки...
В числителе правой части записываем сумму числителей, всё как в числовых дробях, затем раскрываем скобки в числителе правой части, т.е. перемножаем всё и приводим подобные.
Раскрывать скобки в знаменателях, перемножать что-то не нужно! Вообще, в знаменателях (любых) всегда приятнее произведение! Получим:
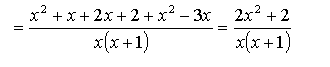
Умножение дробей
Чтобы умножить две обыкновенные дроби, нужно перемножить их числители и знаменатели:
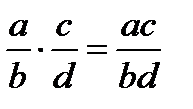
В частности, чтобы умножить дробь на натуральное число, надо числитель умножить на число, а знаменатель оставить тем же:
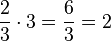
Перед умножением и делением алгебраических дробей, зачастую выгодно разложить их числители и знаменатели на множители — это облегчает сокращение алгебраической дроби, которая получается в результате умножения или деления.
Например:
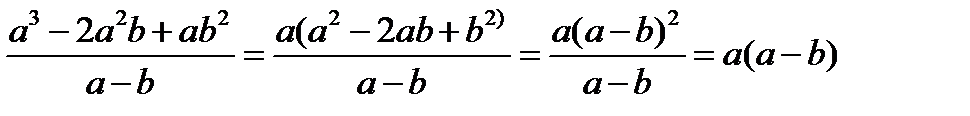
Для разложения алгебраических дробей используются формулы сокращённого умножения (разность квадратов, квадрат разности и тд…):

Деление дробей
Чтобы поделить одну обыкновенную дробь на другую, нужно умножить первую на дробь, обратную второй:
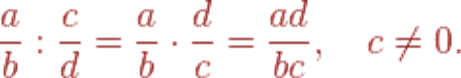
Например
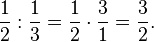
Контрольные вопросы и задания для самостоятельного решения по разделу 1
Ответьте на вопросы:
a) Как избавиться от «трёхэтажности» в обыкновенной дроби?
b) По какому правилу складываются и вычитаются обыкновенные дроби?
c) Как умножить обыкновенные дроби?
d) Как разделить дробь на дробь?
e) Как перевести смешанную дробь в «неправильную»?
Решите упражнения:
№ 1.
1.1) 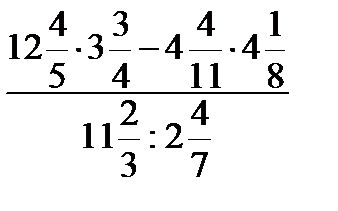 1.2)
1.2) 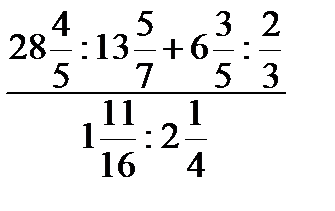
1.3) 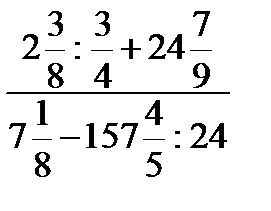 1.4)
1.4) 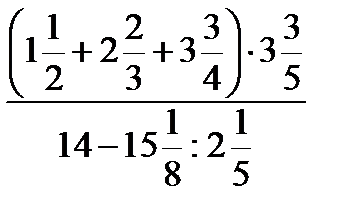
№ 2.
2.1) 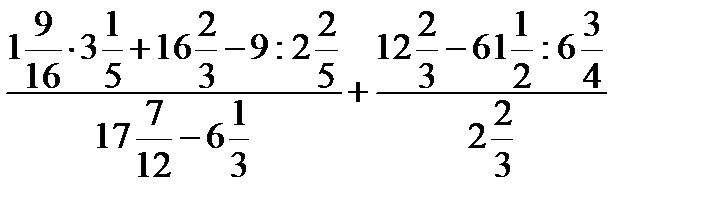
2.2) 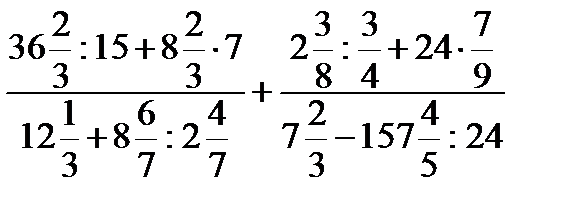
2.3) 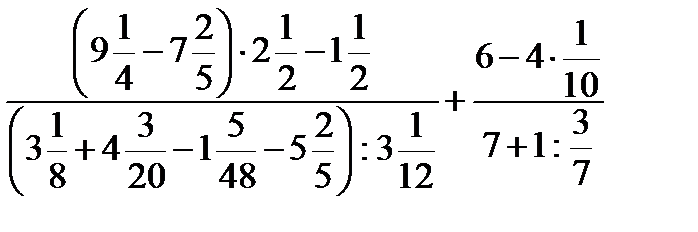
Проверьте своё решение:
Ответы:
1.1) 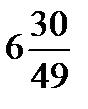 1.2)
1.2) 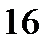 1.3)
1.3) 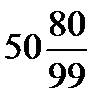 1.4)
1.4) 
2.2) 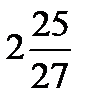 2.3)
2.3)  2.4)
2.4) 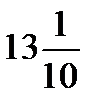
Проценты
Что такое проценты в математике? Как решать задачи на проценты?
Единственно, что нужно запомнить железно – что такое один процент. Это понятие - и есть главный ключ к решению задач на проценты, да и к работе с процентами вообще.
Один процент – это одна сотая часть какого-то числа.
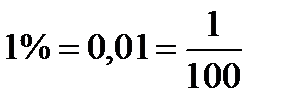
0% = 0; 0,07% = 0,0007; 45,1% = 0,451;
100% = 1; 156% = 1,56; 25% = 0,25
Резонный вопрос – а сотая часть какого числа? А вот того числа, о котором идёт речь в задании. Если там говорится о цене, один процент – это одна сотая часть цены. Если о скорости, один процент – это одна сотая часть скорости. И так далее. Понятно, что само число, о котором идёт речь, составляет всегда 100%. А если нет самого числа, то и проценты смысла не имеют…
Другое дело, что в сложных задачах само число так запрячут, что и не найдёшь.
Например:
Давайте найдём 3% от 400. Сначала найдём один процент. Это будет одна сотая, т.е. 400/100 = 4. Один процент – это 4. А нам сколько процентов надо? Три. Вот и умножаем 4 на 3. Получим 12. Всё. Три процента от 400 – это 12.
5% от 20 это будет 20 поделить на 100 (одна сотая – 1%), и умножить на пять (5%):
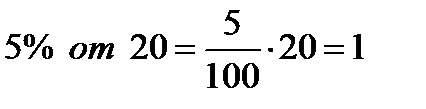 5% от 20 это будет 1.
5% от 20 это будет 1.
А если нам нужно записать х% от какого-то числа, например, от 50? Да всё то же самое. Один процент от 50 – это сколько? Правильно, 50/100 = 0,5. А у нас этих процентов – х. Ну и умножим 0,5 на х! Получим, что
х% от 50 это – 0,5х.


Примеры решения текстовых задач на проценты:
Задача 1.
Проезд на автобусе стоит 14 рублей. В дни школьных каникул для учащихся ввели скидку 25%. Сколько стоит проезд на автобусе в дни школьных каникул?
Решение:
Сколько будет один процент от 14 рублей? Одна сотая часть.
То есть 14/100 = 0,14 рубля. А таких процентов у нас 25.
Умножим 0,14 рубля на 25.
Получим 3,5 рублей. Величину скидки в рублях мы установили, остаётся узнать новую стоимость проезда:
14 – 3,5 = 10,5
Ответ: Десять с половиной рублей.
Задача 2

Контрольные вопросы и задания для самостоятельного решения по разделу 2
Ответьте на вопросы:
1) Что такое процент?
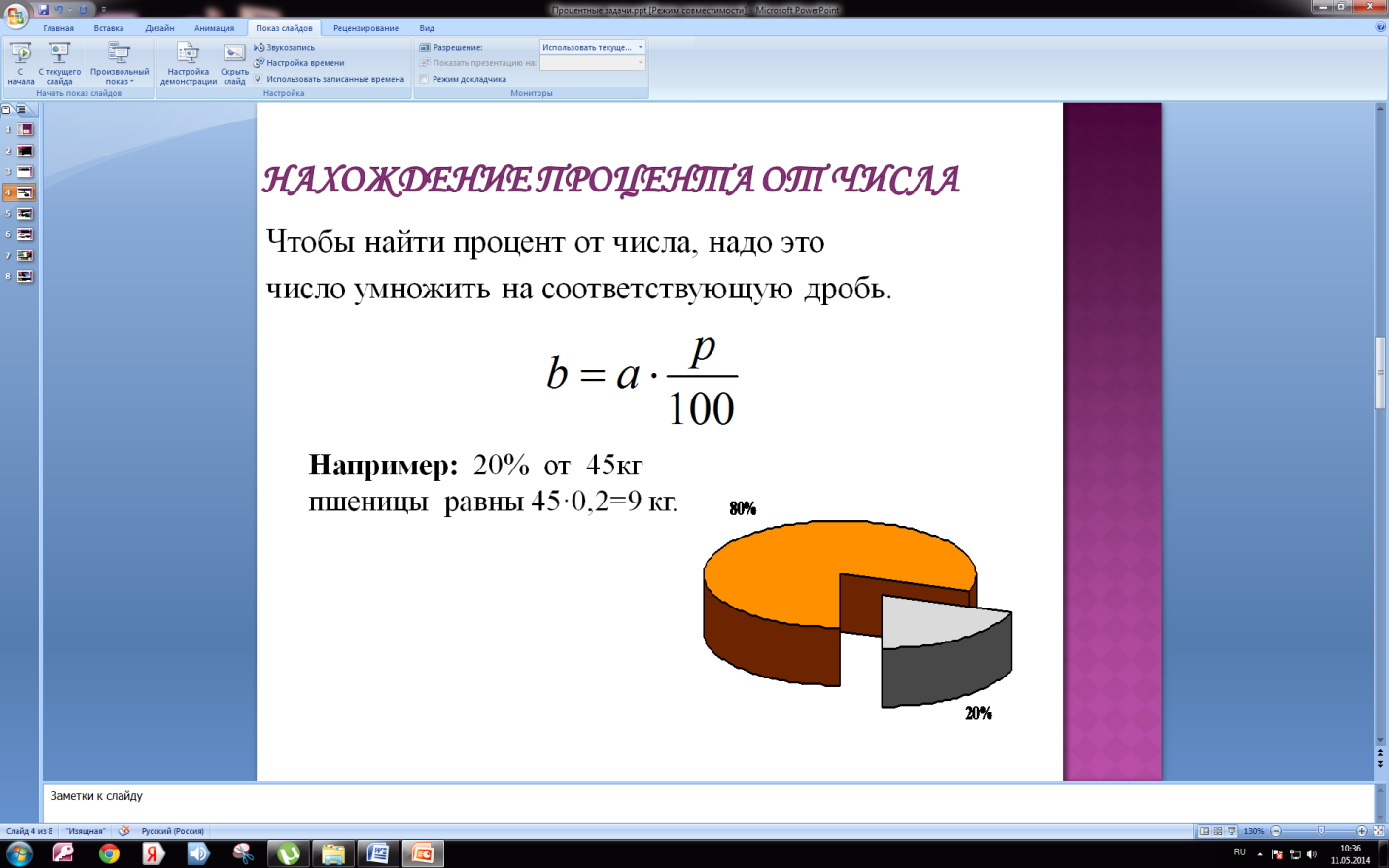
2) Как найти процент от числа?
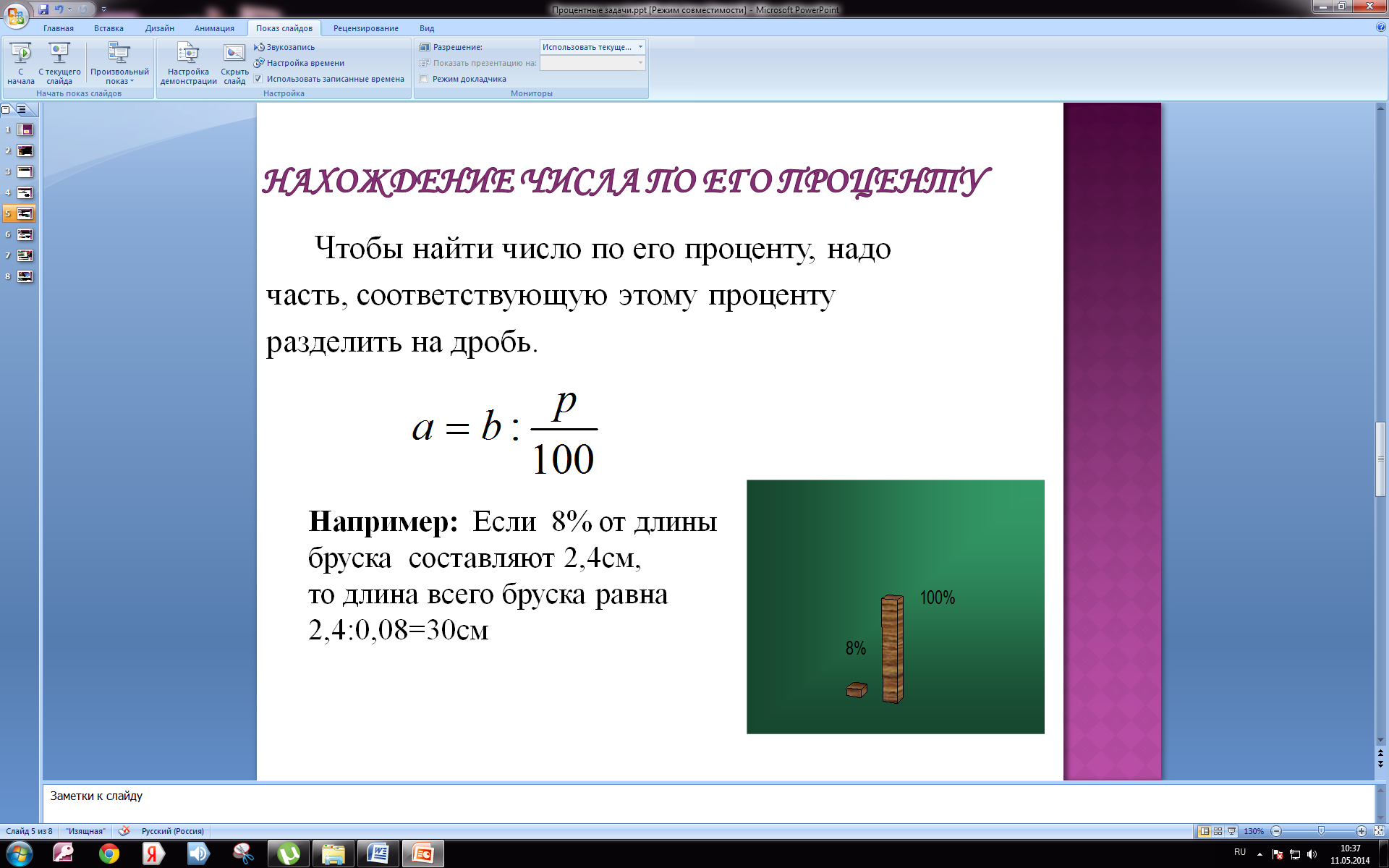
3) Как найти число по его проценту?
Решите упражнения:
1) Футболка стоила 500 рублей. После снижения цены она стала стоить 390 рублей. На сколько процентов была снижена цена на футболку?
2) Футболка стоила 1200 рублей. После снижения цены она стала стоить 972 рубля. На сколько процентов была снижена цена на футболку?
3) Футболка стоила 800 рублей. Затем цена была снижена на 15%. Сколько рублей сдачи с тысячарублёвой купюры должен получить покупатель при покупке этой футболки после снижения цены?
4) Билет на автобус стоит 15 рублей. Какое максимальное число билетов можно будет купить на 100 рублей после повышения цены билета на 20%?
5) Флакон шампуня стоит 200 рублей. Какое наибольшее число флаконов можно купить на 1000 рублей во время распродажи, когда скидка составляет 15%?
6) Шариковая ручка стоит 30 рублей. Какое наибольшее число таких ручек можно будет купить на 700 рублей после повышения цены на 25%?
7) В пачке 250 листов бумаги формата А4. За неделю в офисе расходуется 700 листов. Какое наименьшее количество пачек бумаги нужно купить в офис на 8 недель?
8) В упаковке 16 печек сахара. За неделю кондитерская фабрика расходует 183 пачки. Какое наименьшее количество упаковок сахара нужно купить фабрике на 15 дней?
9) Тетрадь стоит 16 рублей. Сколько рублей заплатит покупатель за 40 тетрадей, если при покупке более 30 тетрадей магазин делает скидку 15% от стоимости всей покупки?
10) На счету Машиного мобильного телефона было 67 рублей, а после разговора с Леной осталось 10 рублей. Сколько минут длился разговор с Леной, если одна минута разговора стоит 1 рубль 50 копеек?
11) Магазин покупает чайники по оптовой цене 420 рублей за штуку, а продает с наценкой 25%. Какое наибольшее число таких чайников можно купить в этом магазине за 3400 рублей?
12) Магазин, делая наценку 50%, продает канцелярские наборы по цене 90 рублей за штуку. Какое наибольшее число таких наборов может закупить хозяин этого магазина на 4300 рублей?
13) В школе есть трехместные туристические палатки. Какое наименьшее число палаток нужно взять в поход, в котором участвует 25 человек?
14) На день рождения полагается дарить букет из нечетного числа цветов. Ромашки стоят 20 рублей за штуку. У Вани есть 250 рублей. Какое наибольшее количество цветов может купить Ваня на эти деньги, чтобы поздравить Машу с днем рождения?
15) Сырок стоит 6 рублей 30 копеек. Какое наибольшее число сырков можно купить на 50 рублей?
16) В пачке 500 листов бумаги формата А4. За неделю в офисе расходуется 800 листов. Какое наименьшее количество пачек бумаги нужно купить в офис на 3 недели?
Проверьте своё решение:
Ответы:
1) на 22% 2) на 19% 3) 320руб. 4) 5
Пачки
