Каналдың өткізгіштік қабілеті

I(X; Y) шамасы ақпараттар теориясында маңызды рөлге ие және байланыс каналы арқылы ақпарат тасымалдау процесін сипаттайды. (7.9) анықтамадан I(X; Y) каналдың өту ықтималдығынан және канал кірісіндегі символдар ықтималдық-тарын бөлуге байланысты.

Алдағы ой жүгіртулер үшін көзге түскен өту ықтималдықты жадсыз дискретті каналды қарастырамыз және өзімізге келесі сауалды қоямыз: Бұл канал арқылы қаншалықты максималды ақпарат тасымалдай аламыз?

Каналдың өткізгіштік қабілеті берілген өту ықтималдықтары менен Х дереккөзі символының барлық кіріс бөлінулеріне тасымалданып жатқан максималды ақпаратқа тең

Ескерту.Өткізгіштік қабілеттің өлшем бірлігі – бит/символ. Мысалы, егер канал арқылы секундына 1 символ тасымалданып жатса, онда сонымен қатар бит/символ өлшем бірлігі турасында да айтуға болады.

Максимум барлық мүмкін дереккөз кірістерінен іздестірілгендіктен, өткізгіштік қабілет каналдың өту ықтималдықтарына тәуелді.

Математикалық тұрғыдан алғанда жадсыз дискретті каналдың өткізгіштік қабілетін іздеу максимум I(X;Y) ақпаратты қамтамасыз ететін дереккөздің кіріс символдарының ықтималдықтарының бөлінуін іздегенмен тең. Солай бола тұра каналдың кіріс х € X символдарының ықтималдықта-рына шектеу қойылады

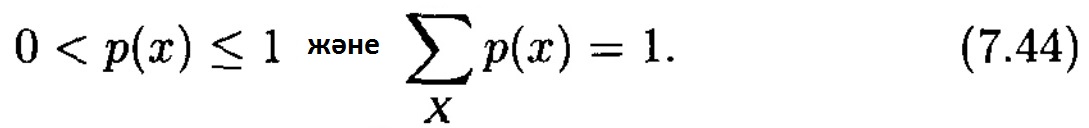
Әсілінде, I(х, у) максимумын (7.44) шектеулер тұсында мультипликатты Лагранж әдісін қолдану арқылы анықтауымыз мүмкін. Бірақ , мұндай шешім шамадан тыс шығынды қажет етеді. Дербес жағдайларда (симметриялы каналдар) өткізгіштік қабілетті табуға келесі теорема [10] жәрдемін тигізеді.

7.5.1 Теорема.Симметриялы жадсыз дискретті каналдарда өткізгіштік қабілетке Х дереккөзінің кіріс символдарының ықтималдықтарын бірқалыпты бөлу арқылы жетеміз.

Ескерту.[10] теоремада канал симметриялы я симметриялы емес екендігін анықтайтын тәсілдер ұсынылған.

Ткізгіштік қабілет

Екілік симметриялы жадсыз дискретті канал (ЕСК) каналдың өті ықтималдықтарының матрицасы арқылы анықталады (7.2). ЕСК сипаттай алатын жалғыз параметр ɛ қате ықтималдығы болып табылады. Канал өткелдерінің символдарының және симметрияларының бірқалыпты бөлінуі шығыс символдарының бірқалыпты бөлінуіне алып келеді, яғни

р(х₁) = p(x₂) = p(y₁) = p(y₂) = 1/2. (7.45)

(7.9) пайдаланып, алатынымыз

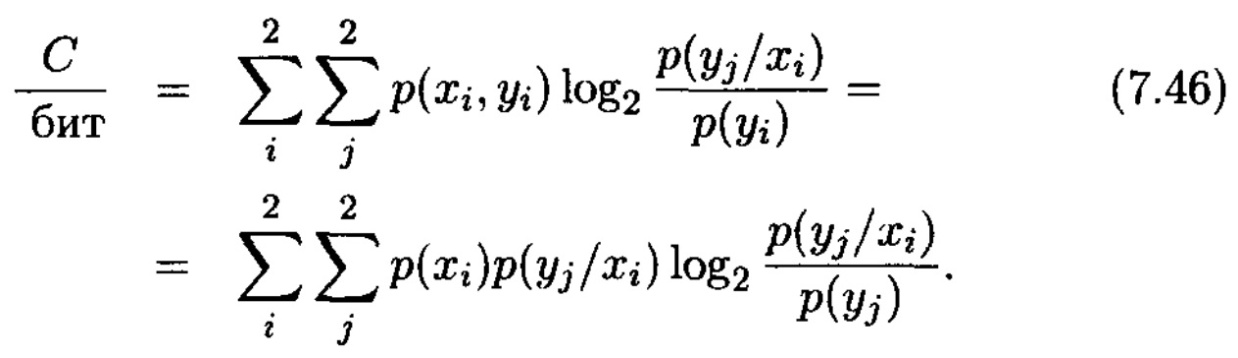
Сандық мәндерін қойғанда, шығады

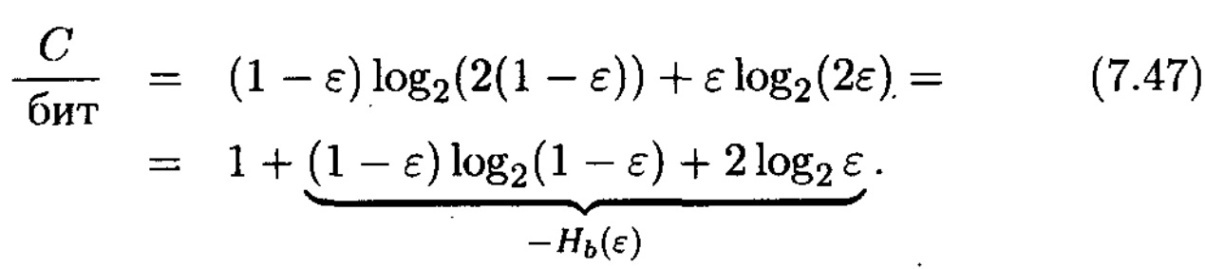
ЕСК энтропиясы (2.32) арқылы анықталады

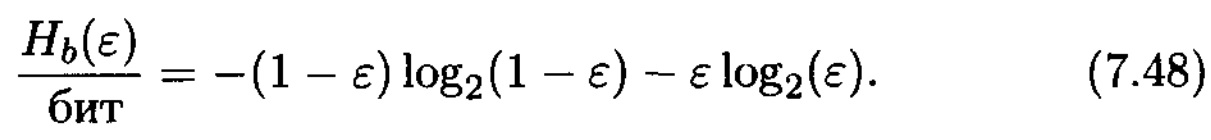
ЕСК өткізгіштік қабілетін жинақы түрде аламыз

С^ДСК = 1 бит - Н_b (ɛ) (7.49)

Екі шектес қызықты жағдай бар:

1. Шусыз канал арқылы ақпарат тасымалдау:

H_b (ɛ = 0) = 0 және C^ЕСК = 1 бит.

2. Канал шуға толы:

H_b (ɛ = 1/2) = 1 және C^ЕСК = 0 бит.

7.5.2. Ақаулы екілік симметриялы каналдың

Ткізгіштік қабілеті

ЕСК-нің маңызды жиі кездесетін жағдайы ақаулы екілік симметриялы канал (АЕСК) немесе ақаулы екілік канал (Binary Erasure Channel, ВЕС - ағыл.). ЕСК секілді ақаулы екілік канал аддитивті ақ гаусс шуы(ААШС) менен канал арқылы ақпарат тасымалдаудың жеңілдетілген үлгісі болып табылады. 7.11 суретте АЕСК-де дұрыс шешім қабылдау ережесі көрсетілген. Суретте жіберілген “0” немесе “1” символдары шешімдерімен қатар мұнда кейде қабылданған “е” (Erasure-ағыл.) символын өшіру шешімі қабылданады. Өшіру детекторланған аналогтық V сигналы тығыз орналасқан шартты функциялардың ықтимал f(V/0) және f(V/1) мәндері нөлге жақын болғандағы зонаға түскен уақытта жүзеге асады.

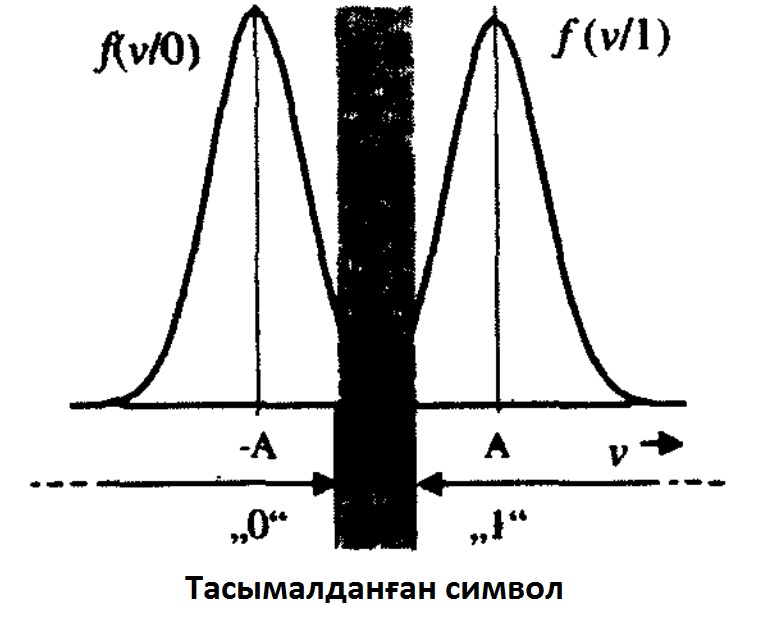
7.11 Сурет.Детекторланған сигналдар ықтималдығының тығыз орналасу

және шешім қабылдау аймағының шартты функцилары.

Ескерту.Ақаулы екілік каналда “0” немесе “1” символдары турасындағы “қатігез” шешімнің орнына “жұмсақ” шешім қабылданады. Бұл жағдайда бізде қабылданған екілік символдың жарамдылығы жайында мағлұматтар бар. Осыған байланысты, мағлұматтар тасымалдау техникасында, “қатігез” және “жұмсақ” шешімдер турасында айтады. “Жұмсақ” шешім сәйкес кодталған мағлұматпен бірлескен түрде кейбір жағдайларда артығырақ жарамды мағлұмат тасымалдауға септігін тигізеді. “Жұмсақ” шешімді қолданатын мысалды осы кітаптың екінші бөлімінен таба аласыз.

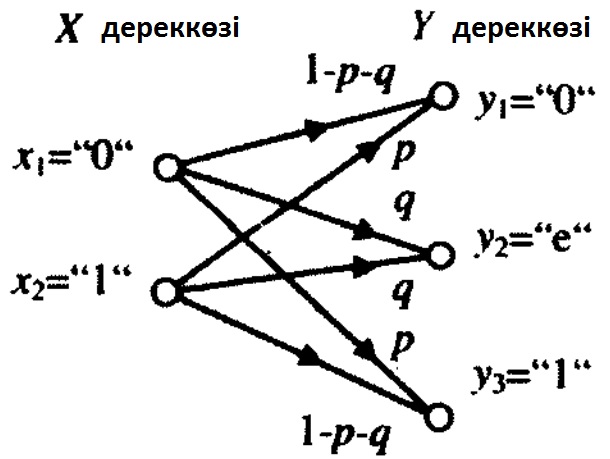
7.12 Сурет.Ақаулы екілік симметриялы канал.

Өшіру ықтималдығын q арқылы, ал өшірілмеген символдың қате ықтималдығын р арқылы белгілейік.

Екі кірісті және үш шығысты символы бар каналдар үшін өті диаграммасы 7.12 суретте көрсетілген. Өту ықтималдықтары бар сәйкес матрицалы канал мына түрде болады

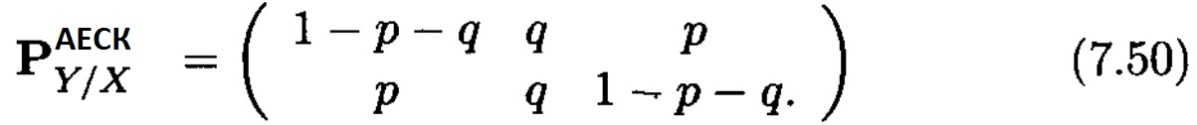
Ақаулы каналдың өткізгіштік қабілетін табамыз. Канал симметриялы болғандықтан, өткізгіштік қабілетке кіріс символдарының бірқалыпты бөлінуі арқылы жетеміз

р(х₁) = р(х₂) = 1/2. (7.51)

Бұл жерден білетініміз, шығыс символдарының ықтималдықтары тең

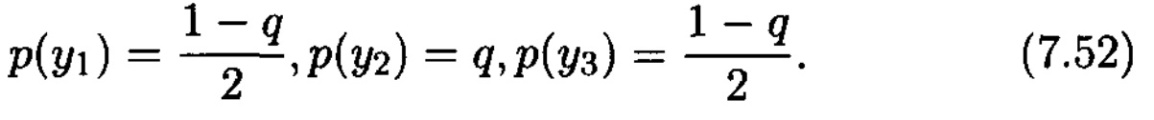
Енді барлық керекті ықтималдықтар мәлім. (7.9) қолданып алатынымыз

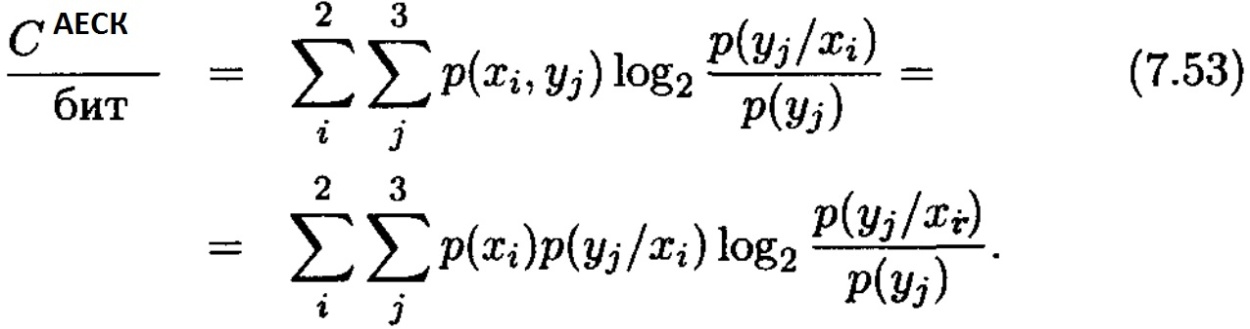
Канал симметриясының қасиетін пайдаланып, алатынымыз

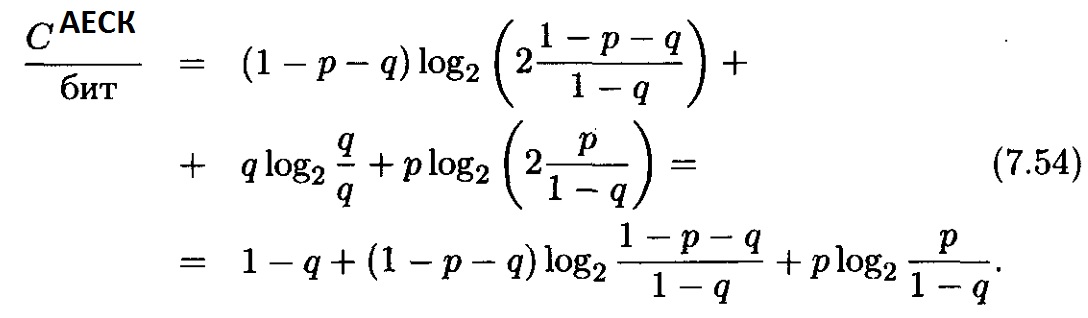
Көріп тұрғанымыздай ақаулы каналдың өткізгіштік қабілеті р және q ықтималдықтарына тәуелді. С = f(р, q) графигі өзімен жазықтық (p, q) үстінде орналасқан үш өлшемді кеңістікті ұсынады. Бұл жерде біз екі маңызды жағдайды қарастырумен шектелеміз.

1. q = 0 болғанда, бізде алдын қарастырылған айтарлықтай симметриялы канал бар. (7.59)-ға q = 0 қойып, күткеніміздей, (7.49) аламыз.

2. Каналда тек ақаулар бар, яғни р = 0 болғанда – қателер я жоқ я болмаса біз оларды ескермей жатырмыз. Бұл жағдайда

С ^ЕАКС = (1 - q) бит. (7.55)

7.13 суретте ЕСК-ның (7.49) және ақаулы екілік каналдың (p = 0) өткізгіштік қабілеттері көрсетілген. Түртіп өткен жөн, қатенің төмен ықтималдықтарында ЕАКС-да ақаудың оптималды аймақтарын таңдаумен, қарапайым екілік каналдарға қарағанда елеулі өткізгіштік қабілетке жетуге болады.

Ескерту.Бұл жерде ақаулармен қабылдағандағы өткізгіштік қабілетті практикада арттыру мүмкіншіліктері хақында сұрақ туындайды. Мұнда ақпараттық теорияның әлсіз екендігі білінеді. Ақпараттар теориясы әдетте теоретикалық түрде қол жетімді шекке жететін конструкцияны ұсына алмайды. Дегенмен, осы кітаптың екінші бөлімінде қаралған мысал ақау енгізу кейде қате ықтималдығын төмендететінін көрсетеді. Бұл мысалды интуитивті дәрежеде қарастырайық. Тасымалданып жатқан ақпарат тасқынын 7 екілік символдардан (7 бит) тұратын блоктарға бөлейік. Әр блокқа жұп екенін тексеру үшін бір бит (“0” немесе “1”) қосамыз. Мұндай тәсілмен кодталған сегіз екілік символдан тұратын блоктар әрдайым жұп санды ұстайды. ЕСК-дағы қате ықтималдығы айтарлықтай төмен болсын. Ақау аймағын (7.11 сурет), қателер, негізінен, ақауларға өтетіндей тәсілмен енгіземіз. Сондықтан, “өшірілмеген” қате ықтималдығы өте төмен болады, ал ақау ықтималдығы дерліктей төмен болып қала береді.

Біз, құзырында сегіз екілік символдан тұратын блоктар көп жағдайда я дұрыс қабылданатын я болмаса тек бір өшірілген екілік символы болатын ақаулы канал (EACK) аламыз. Қабылдау сапасы дерліктей жоғарылайды, себебі жұп бірлік санды блоктағы ақауды әр уақытта түзетсе болады.

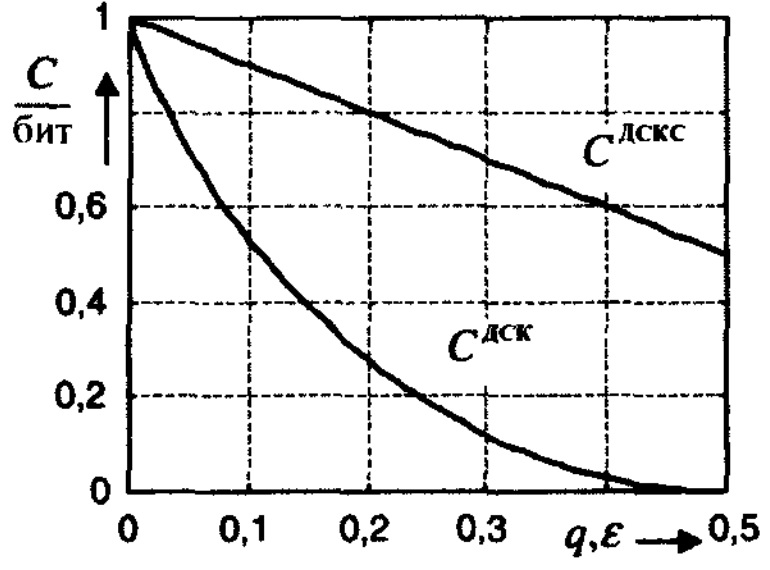
7.13 Сурет.ɛ қате ықтималдықты екілік симметриялы каналдың С^ЕСК

және p=0 қате ықтималдықты һәм q ақау ықтималдықты

ақаулы екілік каналдың С^ЕАСК өткізгіштік қабілеті.

Мысал:Ақаулы екілік симметриялы канал.

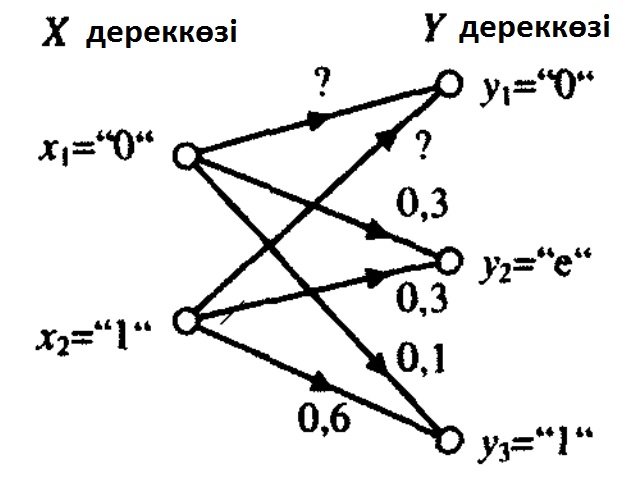
7.14 Сурет.Ақаулы екілік канал.

7.14 суретте ақаулы симметриялы каналдың өті диаграммасы берілген.

Анықтаңыздар:

1. Канал матрицасын;

2. Егер Х дереккөзінің символдары бірқалыпты бөлінген болса, Ү

дереккөзінің символдар ықтималдығын бөлу, яғни р₀ = p₁ = 1/2;

3. Каналдың өткізгіштік қабілетін;

4. Барлық энтропиялы ақпараттық тасқындар диаграммасын;

5. Р_X/Y матрицалы канал үлгісін.

Шешуі.

1. Матрицаның әр қатарындағы ықтималдықтар суммасы 1-ге тең екенін есепке ала отырып, алатынымыз

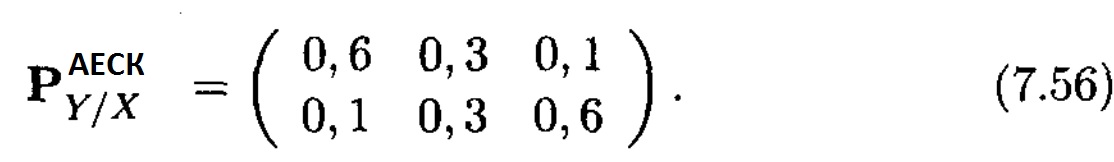
2. Кірістегі символдар ықтималдықтарының бірқалыпты бөлінуі нәтижесінде, (7.52) сәйкес, шығады

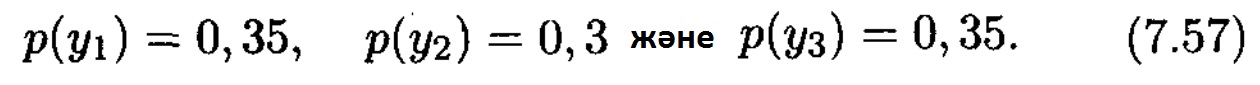
3. Қарастырылып жатқан канал симметриялы болғандықтан, өткізгіштік қабілетке кіріс символдарының бірқалыпты бөлінуі нәтижесінде жетеміз. (7.56) есепке алып (7.54) шығатыны

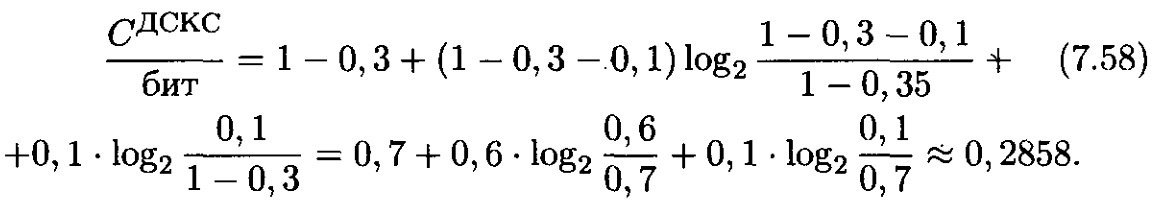
4. Жадсыз дискретті екілік Х дереккөзінің энтропиясының символдары ықтималдықтарының бірқалыпты бөлінуі нәтижесінде

Н(Х) = 1 бит. (7.59)

Ү дереккөзінің энтропиясы мынаған тең

Симметриялы каналда кіріс I(X;Y) символдарының бірқалыпты бөлінуі (7.58)-дегі С өткізгіштік қабілетімен тура келгендіктен, бірлескен және екі шартты энтропияны (7.3) кестені қолданып есептеуге болады.

Ақпараттық тасқындар диаграммасы 7.15 суретте көрсетілген

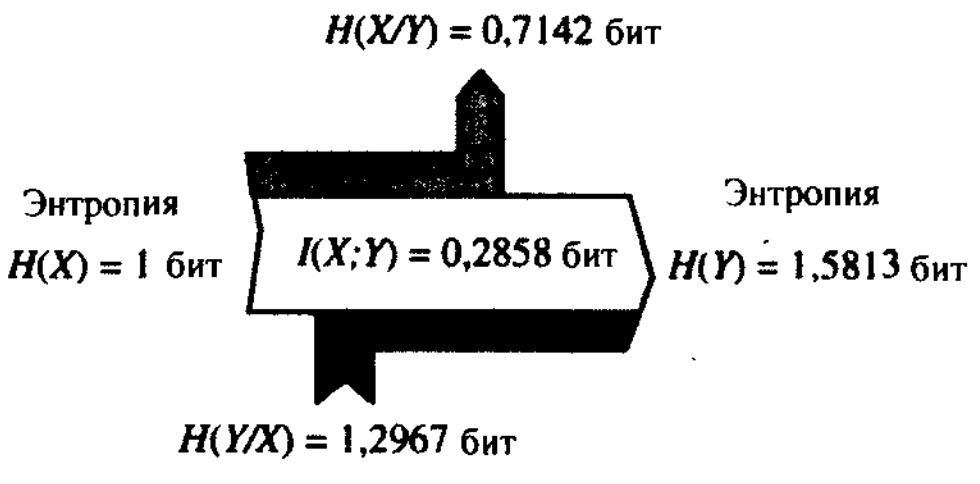
7.15 Сурет.Ақаулы екілік симметриялы каналдың ақпараттық

тасқындар диаграммасы

5. Р_Ү/Х каналының өту ықтималдықтарының матрицасын Р_Х/Ү матрицасына қайта есептеуді оқырманға дербес жаттығу ретінде орындауды талап етеміз. Ү кіріс және Х шығыс дереккөзінің канал диаграммасы 7.16 суретте бақылау үшін көрсетілген.

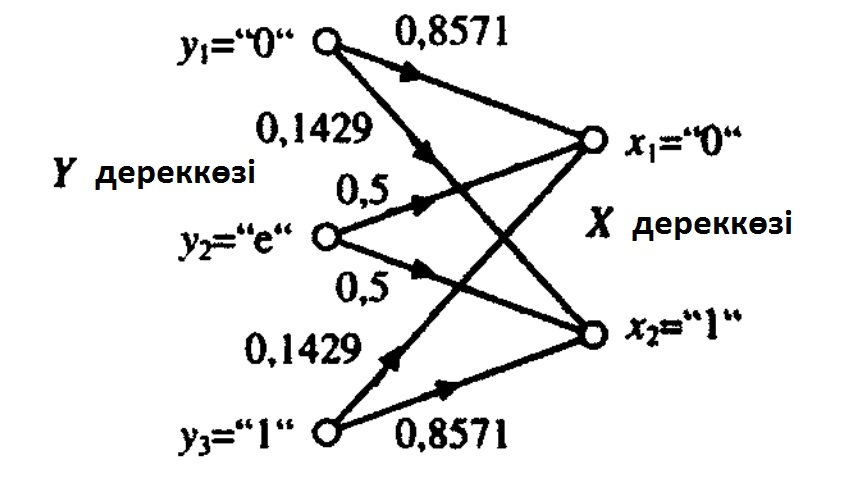
7.16 Сурет.Ақаулы екілік симметриялы канал.