Плоскость и прямая в пространстве. Пример. Даны четыре точки:

Пример. Даны четыре точки: .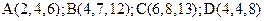

Найти: 1) уравнение прямой ( 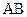) в канонической форме;

2) уравнение прямой (R), проходящей через точку 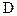параллельно прямой ( ) ;

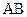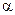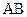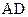3) тупой угол между прямыми ( ) и ( ), т.е.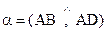

4) уравнение плоскости ( );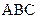

5) угол 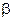между прямой ( 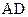) и плоскостью ( );

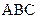6) уравнение прямой ( L), проходящей через ;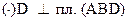

7) угол 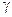между плоскостью ( 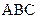) и плоскостью ( );

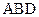8) уравнение плоскости (Q), проходящей через точку ;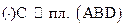

Решение.

1) На прямой АВ известны две точки, поэтому найдём её как прямую, проходящую через две точки:

(АВ):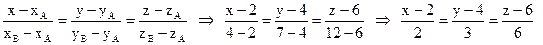

(АВ): 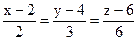- задание прямой в канонической форме,

причём её направляющий вектор .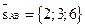

2) Прямая .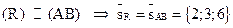

Знаем одну точку на прямой 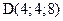и направляющий вектор этой прямой, поэтому прямую можно задать в канонической форме: .

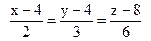3) Направляющий вектор (АВ): 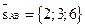, а в качестве направляющего вектора (AD) можно использовать вектор .

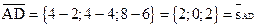Угол между этими прямыми найдём по формуле: ,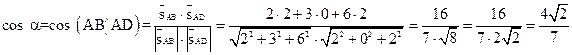

Тогда .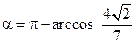

4) Уравнение плоскости АВС, проходящей через три данные точки, можно найти по формуле:

.

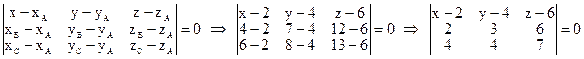Разложив определитель по первой строке, получим: .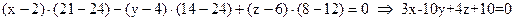

(АВС): 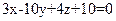- уравнение плоскости (АВС) в общем виде,

причём 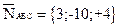-её нормальный вектор.

5) Угол между прямой (AD) и плоскостью (АВС) найдём по формуле

.

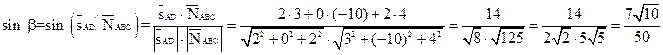6) Найдём уравнение плоскости (ABD):

(ABD):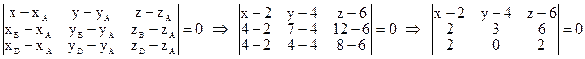

Разложив определитель по первой строке, получим: .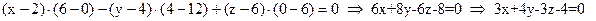

(АВD): 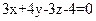- уравнение плоскости (АВD) в общем виде,

причём 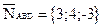- её нормальный вектор.

Если прямая перпендикулярна плоскости, то её направляющим вектором может быть нормальный вектор плоскости, т.е. .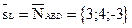

Теперь прямую L можно задать как прямую, проходящую через данную точку в данном направлении:

(L): .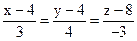

7) .

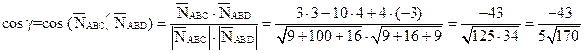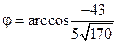. Косинус отрицательный, следовательно, угол – тупой.

8) Плоскость Q параллельна плоскости (ABD), поэтому нормальные векторы у них могут быть одинаковыми: .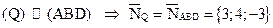

Воспользуемся уравнением плоскости, проходящей через данную точку С(6;8;13) перпендикулярно данному направлению: 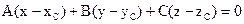, где А, В, С – координаты нормального вектора плоскости Q.

Тогда (Q): .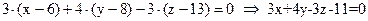

Контрольная работа 1

Линейная алгебра

Система трёх линейных уравнений с тремя неизвестными х₁, х₂, х₃

Задана своей расширенной матрицей.

Требуется:

Записать систему в канонической форме (в виде системы уравнений),

2) решить её методом полного исключения,

3) решить эту же систему по формулам Крамера, причём определители вычислять,

Используя их свойства.

№	Расширенная матрица	№	Расширенная матрица
1.01		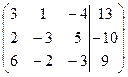1.11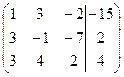
1.02		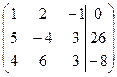1.12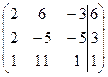
1.03		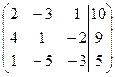1.13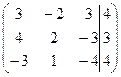
1.04		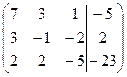1.14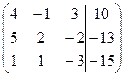
1.05		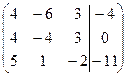1.15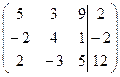
1.06		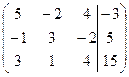1.16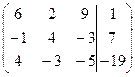
1.07		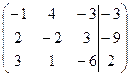1.17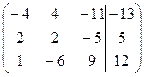
1.08		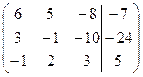1.18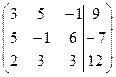
1.09		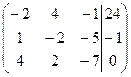1.19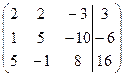
1.10		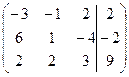1.20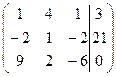

Векторная алгебра

Даны координаты вершин пирамиды A, B, C, Q, причём точки A, B, C - вершины её основания.

Средствами векторной алгебры найти:

Векторы с началом в точке A и концом в остальных вершинах пирамиды;

2) длину этих векторов и направляющие косинусы вектора ;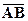

3) скалярное произведение векторов 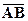и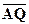

4) угол между рёбрам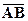и и ;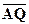

5) векторное произведение векторов 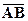и 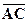;