Построение линейной регрессионной модели по выборочным данным

Рассмотрим построение линейной регрессионной модели по выборочным данным следующего примера.

Пример. В табл. 2.1 приведены данные по 45 предприятиям по статистической связи между стоимостью основных фондов (fonds, млн. денежных единиц) и средней выработкой на 1 работника (product, тыс. денежных единиц); z – вспомогательный признак: z = 1 – федеральное подчинение, z = 2 – муниципальное.

Таблица 2.1

fonds	product	z	fonds	product	z	fonds	product	z
6,5	18,3		9,3	17,2		10,4	21,4
10,3	31,1		5,7	19,0		10,2	23,5
7,7	27,0		12,9	24,8		18,0	31,1
15,8	37,9		5,1	21,5		13,8	43,2
7,4	20,3		3,8	14,5		6,0	19,5
14,3	32,4		17,1	33,7		11,9	42,1
15,4	31,2		8,2	19,3		9,4	18,1
21,1	39,7		8,1	23,9		13,7	31,6
22,1	46,6		11,7	28,0		12,0	21,3
12,0	33,1		13,0	30,9		11,6	26,5
9,5	26,9		15,3	27,2		9,1	31,6
8,1	24,0		13,5	29,9		6,6	12,6
8,4	24,2		10,5	34,9		7,6	28,4
15,3	33,7		7,3	24,4		9,9	22,4
4,3	18,5		13,8	37,4		14,7	27,7

Предварительно построим диаграмму рассеяния, чтобы убедиться, что предположение линейности регрессионной зависимости не лишено смысла. Для этого в меню Graphs выберем команду Scatter plots. В полученном окне нажмем кнопку Variables., и установим зависимые данные – X: fonds, Y: product и опции графика – Graphs Type: Regular, Fit (подбор): Linear.

Наблюдаем диаграмму рассеяния с подобранной прямой регрессии, параметры которой отражены в ее заголовке. Это означает, что уравнение линейной регрессии имеет вид .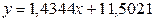

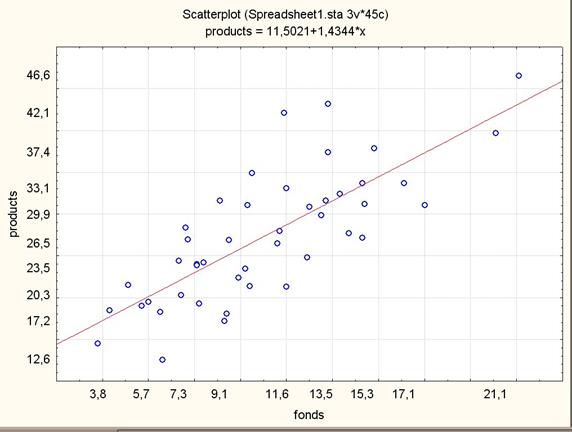
Рис. 2.1. Диаграмма рассеяния

Чтобы получить обратную зависимость, в окне задания опций следует поменять местами переменные X и Y, то есть переменной X назначить колонку products, а переменной Y – fonds. В этом случае уравнение регрессии задается уравнением 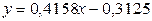, а прямая имеет вид, представленный на рис. 2.2.

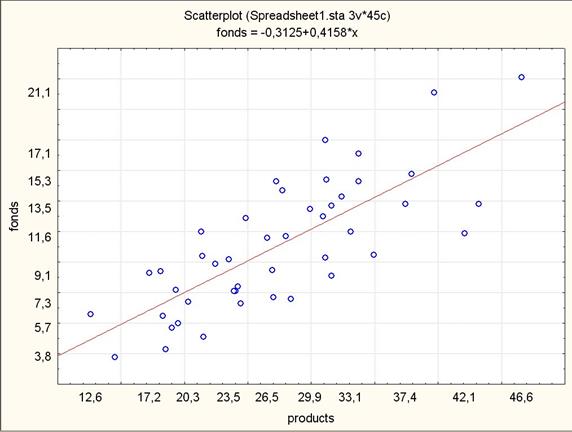
Рис 2.2. Обратная диаграмма рассеяния

По полученным графикам делаем вывод, что имеет смысл проводить регрессионный анализ по имеющимся исходным данным.

Будем работать в модуле Multiple Regression (множественная регрессия); меню Statistics – Multiple Regression. В качестве зависимой переменной выберем колонку fonds, в качестве независимой – колонку products, во вкладке Advanced установим опцию Input file (входной файл): Raw Data (необработанные данные).

Нажав кнопку OK, получаем основные результаты анализа (рис. 2.3) коэффициент детерминации R²: 0.597; гипотеза о нулевом значении наклона отклоняется с высоким уровнем значимости p = 0.000000 (т.е. p < 10^-6).

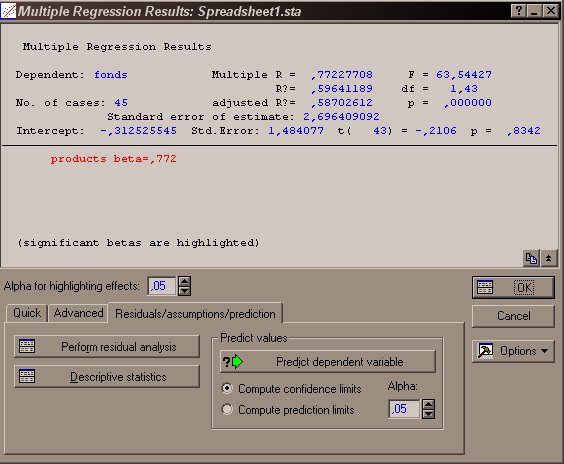
Рис. 2.3. Окно результатов регрессионного анализа

Поясним значения характеристик:

Dependent – имя зависимой переменной (в примере – fonds);

Multiple R – множественный коэффициент корреляции;

F – значение критерия Фишера, F=63, 54427;

R? (R²) – множественный коэффициент детерминации;

df – количество степеней свободы F-критерия;

No. of cases – количество наблюдений;

adjusted R? (R²) – скорректированный коэффициент детерминации, определяемый по формуле ;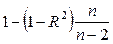

p – критический уровень значимости модели;

Standard error of estimate – среднеквадратическая ошибка;

Intercept – оценка свободного члена модели регрессии;

Std. Error – стандартная ошибка оценки свободного члена модели регрессии;

t(43) = -0,2106 и p = 0,8342 – значения критерия и критического уровня значимости, используемые для проверки гипотезу о равенстве нулю свободного члена регрессии. В данном случае гипотеза должна быть принята, если уровень значимости равен 0,8342 или ниже.

На вкладке Quick нажмем кнопку Summary Regression Results и получим таблицу результатов (рис. 2.4).

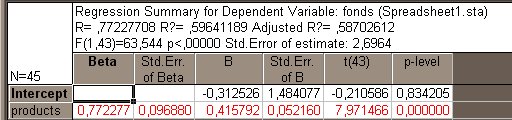
Рис. 2.4. Таблица результатов регрессионного анализа

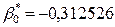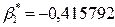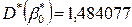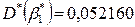В заголовке полученной таблицы повторены результаты предыдущего окна; в столбцах приведены: В – значения оценок параметров модели регрессии и ; столбец St. Err. of B – параметры стандартных ошибок параметров модели регрессии, соответственно и ; столбец t(43) – значение статистики Стьюдента (t-критерия) для проверки гипотезы о нулевом значении коэффициента (т.е. 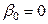и 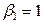); столбец p-level – минимальный уровень значимости отклонения этой гипотезы. В данном случае, поскольку значения p-level очень малы (меньше 10^-4), гипотезы о нулевых значениях коэффициентов отклоняются с высокой значимостью. Итак, имеем регрессию:

product = 11.5 + 1.43 fonds,

соответствующие стандартные ошибки коэффициентов: 2.1 и 0.18; значение s = 5.01 (Std Error of estimate – ошибка прогноза выработки по фондам с помощью этой функции). Значение коэффициента детерминации R² = RI = 0.597 достаточно велико (доля R = 0.77 всей изменчивости объясняется вариацией фондов). Уравнение регрессии показывает, что увеличение основных фондов на 1 млн. денежных единиц приводит к увеличению выработки 1 работника в среднем на b₁ = 1.43 тыс. денежных единиц.

Многочисленные дополнительные опции модуля регрессии позволяют, например, вычислить результаты описательной статистики (среднее значение и среднее квадратическое отклонение), а также коэффициент корреляции между данными. Для этого можно воспользоваться вкладкой Advanced, нажав на ней кнопку Descriptive Statistics и выбрав необходимые кнопки. Результат будет отображен в отдельном окне. Нажав на кнопку во вкладке Matrix, получим общее окно, приведенное на рис. 2.5.

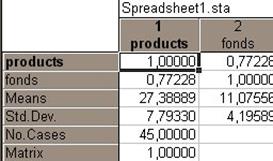
Рис. 2.5. Описательная статистика и коэффициент корреляции