Надежность подшипников качения
Применяемые во всем мире и в России расчеты подшипников качения были первыми вероятностными расчетами машиностроительных объектов. Но они учитывают рассеяние только динамической грузоподъемности подшипников в предположении детерминированности расчетной нагрузки.
Ниже ставится задача изложить вероятностный расчет подшипников в общей форме, аналогичной форме, принятой для других деталей.
Вероятность безотказной работы отождествляем с вероятностью выполнения известного условия 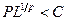 , где Р – динамическая эквивалентная нагрузка; С – динамическая грузоподъемность; L – заданный ресурс; р – показатель степени, равный 3 для шарикоподшипников и 10/3 для роликоподшипников.
, где Р – динамическая эквивалентная нагрузка; С – динамическая грузоподъемность; L – заданный ресурс; р – показатель степени, равный 3 для шарикоподшипников и 10/3 для роликоподшипников.
В отличие от обычных расчетов рассматриваем Р как случайную величину. 90%-ную динамическую грузоподъемность, значение которой приводят в каталогах и справочниках, обозначим 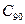 . Среднее значение динамической грузоподъемности принимаем равным:
. Среднее значение динамической грузоподъемности принимаем равным: 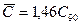 для роликоподшипников и
для роликоподшипников и 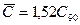 для шарикоподшипников (обоснование рекомендации приведено ниже).
для шарикоподшипников (обоснование рекомендации приведено ниже).
Полагаем, что динамическая эквивалентная нагрузка и динамическая грузоподъемность распределены по нормальному или близкому к нормальному закону. Тогда вероятность безотказной работы определяем по квантили нормированного нормального распределения
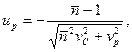
где 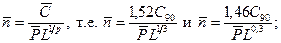
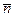 – коэффициент запаса по средним нагрузкам; С – среднее значение динамической грузоподъемности; Р – среднее значение динамической эквивалентной нагрузки;
– коэффициент запаса по средним нагрузкам; С – среднее значение динамической грузоподъемности; Р – среднее значение динамической эквивалентной нагрузки; 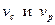 – коэффициенты вариации динамической грузоподъемности и динамической эквивалентной нагрузки.
– коэффициенты вариации динамической грузоподъемности и динамической эквивалентной нагрузки.
Среднее значение динамической эквивалентной нагрузки Р вычисляют по обычным зависимостям, в которые подставляют средние значения радиальной и осевой нагрузок, действующих на подшипник.
Коэффициент вариации динамической эквивалентной нагрузки 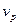 принимаем равным коэффициенту вариации внешней нагрузки, действующей на подшипник. Рекомендация основана на равенстве коэффициентов вариации случайных величин, связанных между собой линейной зависимостью.
принимаем равным коэффициенту вариации внешней нагрузки, действующей на подшипник. Рекомендация основана на равенстве коэффициентов вариации случайных величин, связанных между собой линейной зависимостью.
Коэффициент вариации динамической грузоподъемности принимают 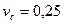 для роликоподшипников и
для роликоподшипников и 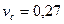 для шарикоподшипников.
для шарикоподшипников.
Основой для рекомендаций по выбору закона и параметров распределения динамической грузоподъемности послужило широко принятое предположение о распределении ресурса подшипников по закону Вейбулла. В соответствии с этим законом связь между вероятностью безотказной работы 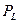 и ресурсом L выражается зависимостью
и ресурсом L выражается зависимостью 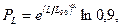 где
где 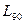 – 90%-ный ресурс;
– 90%-ный ресурс; 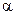 – параметр формы распределения Вейбулла, связанный с рассеянием ресурса (
– параметр формы распределения Вейбулла, связанный с рассеянием ресурса ( 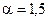 ).
).
В расчетах подшипников качения отношение 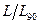 называют коэффициентом надежности
называют коэффициентом надежности 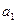 который определяют по формуле, вытекающей из предыдущего выражения:
который определяют по формуле, вытекающей из предыдущего выражения:
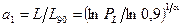
Учитывая, что между ресурсом L и динамической грузоподъемностью С существует соотношение 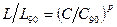 получаем
получаем
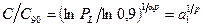
Структура зависимости С от 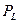 указывает, что динамическая грузоподъемность, так же как и ресурс, распределена по закону Вейбулла. Однако для инженерных расчетов распределение динамической грузоподъемности можно аппроксимировать нормальным законом, что резко упрощает вероятностные расчеты.
указывает, что динамическая грузоподъемность, так же как и ресурс, распределена по закону Вейбулла. Однако для инженерных расчетов распределение динамической грузоподъемности можно аппроксимировать нормальным законом, что резко упрощает вероятностные расчеты.
При аппроксимации среднее значение динамической грузоподъемности 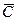 принимаем равным медианному (50%-ному) значению
принимаем равным медианному (50%-ному) значению 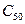 , что с учетом (11) приводит к соотношению
, что с учетом (11) приводит к соотношению
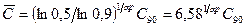
Среднее квадратическое отклонение динамической грузоподъемности 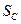 определяем через разность 50%-ной
определяем через разность 50%-ной 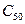 и 90%-ной
и 90%-ной 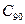 квантилей, с учетом
квантилей, с учетом 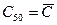 , получаем
, получаем
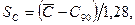
где постоянная 1,28 – 90%-ная квантиль нормированного нормального распределения.
Коэффициент вариации динамической грузоподъемности
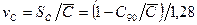
Подставляя в (12) и (13) значения 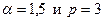 (для шарикоподшипников) или
(для шарикоподшипников) или 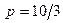 (для роликоподшипников), получаем приведенные выше значения параметров нормального распределения динамической грузоподъемности.
(для роликоподшипников), получаем приведенные выше значения параметров нормального распределения динамической грузоподъемности.
Рекомендации по выбору для роликоподшипников параметра 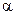 формы распределения ресурса совпадают, т.е.
формы распределения ресурса совпадают, т.е. 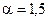 . Для шарикоподшипников ИСО рекомендует принимать
. Для шарикоподшипников ИСО рекомендует принимать 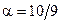 , что соответствует среднему значению динамической грузоподъемности
, что соответствует среднему значению динамической грузоподъемности 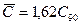 и коэффициенту вариации
и коэффициенту вариации 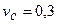 .
.
Уточнение расчетных зависимостей для подшипников качения связано с дифференцированным учетом влияния таких факторов, как требуемая надежность подшипника, материал деталей, режим смазки.
В обычных расчетах это учитывается введением в формулу, определяющую ресурс подшипника, корректирующих коэффициентов: 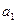 – коэффициента надежности,
– коэффициента надежности, 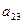 – объединенного коэффициента материала и режима смазки (рассматривается раздельно коэффициент материала
– объединенного коэффициента материала и режима смазки (рассматривается раздельно коэффициент материала 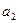 и коэффициент режима смазки
и коэффициент режима смазки 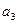 ).
).
В предлагаемой форме расчета влияние рассматриваемых факторов учитывается введением в формулу (12), определяющую средние значения динамической грузоподъемности, дополнительного сомножителя 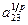 .
.
Следующим возможным направлением уточнения вероятностных расчетов подшипников качения является учет экспериментально установленного факта непостоянства коэффициента вариации ресурса 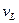 , в частности его увеличения при росте медианного значения ресурса
, в частности его увеличения при росте медианного значения ресурса 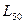 [15].
[15].
В предположении описания ресурса законом Вейбулла учет непостоянства коэффициента вариации ресурса 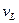 , приведет к пересмотру рекомендаций по выбору значения параметра формы
, приведет к пересмотру рекомендаций по выбору значения параметра формы 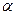 , так как между
, так как между 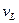 и
и 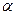 существует функциональная зависимость, где параметр формы обозначен через m). Следует ожидать, что с ростом медианного значения ресурса, например вследствие улучшения технологии изготовления подшипников, уменьшится значение коэффициента формы
существует функциональная зависимость, где параметр формы обозначен через m). Следует ожидать, что с ростом медианного значения ресурса, например вследствие улучшения технологии изготовления подшипников, уменьшится значение коэффициента формы 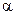 .
.
