Жылдамдық потенциалы және оның ток функциясымен байланысы

Бұрыштық жылдамдығының компоненттері нөлге тең болғандағы қозғалыс алдында құйынсыз ағыс деп анықталды, сондықтан 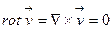және (3.13) теңдіктері орынды.

Екінші жағынан, егер бірінші және екінші үзіліссіз туындылары бар, кейбір 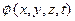скаляр функциясы болса, онда векторлық талдауынан белгілі 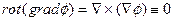. Бұган қажетті дифференциалдау операцияларын орындаған жағдайда көз жеткізуге болады. Сондықтан құйынсыз қозғалыста градиенті оның 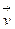жылдамдық векторына тең, скаляр функциясы 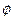болу керек. Бұл скаляр функциясы азайатын ағыс бағытын оң деп есептеу қабылданған

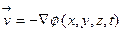. (3.14)

Теріс градиент 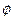жылдамдық векторына тең болғандықтан, 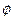функциясы жылдамдық потенциалы деп аталады, ал құйынсыз ағынды жиі потенциалды ағын дейді. Құйынсыз қозғалыс жағдайда сығылатын да, сығылмайтын да сұйықтықтар болуы мүмкін және осы әр жағдайда да жылдамдықтың потенциал функциясы бар болады.

Сығылмайтын сұйықтық ағысы үшін үзіксіздік теңдеуі бойынша

.

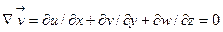Сондықтан, 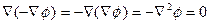. (3.15)

Алынған теңдеу Лаплас теңдеуі болып табылады, дифференциалдық оператор 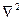лапласиан деп аталады және декарт координаталарында мына түрде болады

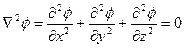; (3.16)

Сығылмайтын сұйықтықтың екіөлшемді құйынсыз ағысы үшін жылдамдық потенциалы және ток функциясы анықталған байланыста болады.

(3.14) өрнегінің декарт координаталар өстеріне проекцияларын қарастырсақ, табамыз

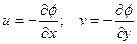. (3.17)

(3.9) өрнегін ескере отырып, аламыз

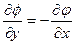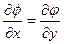; . (3.18)

Бұл теңдеулер Коши – Риман шарты ретінде белгілі. Оларды иірімділік жоғын көрсететін теңдеуге 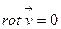немесе екіөлшемді қозғалыс үшін 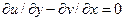теңдеуіне қойсақ, табамыз 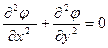, яғни ток функциясы Лаплас теңдеуін қанағаттандырады.