Статическим методом В.З. Власова

При ипользовании для расчета пластин метол Бубнова – Галеркина прогиб пластины задается в виде [4]

, (4)

где B_i - неизвестные коэффициенты, x_i(ξ)- характер прогиба пластины в направлении оси ξ, который должен удовлетворять заданным граничным условиям на сторонах пластины ξ=0, ξ=1, а y_i(h)характер прогиба пластины в направлении оси h, который должен удовлетворять заданным граничным на сторонах пластины h=0, h=1.

В методе Бубнова - Галеркина функции x_i(ξ) и y_i(h), которые в дальнейшем называем аппроксимирующими (приближающими), должны удовлетворять всем граничным условиям.

Если взять достаточное число членов ряда n в (4), то можно получить достаточно точное решение задачи методом Бубнова – Галеркина. Однако при большом числе членов ряда прогиба w (4) значительно возрастает трудоемкость решения задачи методом Бубнова – Галеркина. В связи с этим желательно использовать такие способы построения функций x(ξ) и y(h), при которых они достаточно отражают характер прогиба пластины по направлениям осей ξ и h и задачу можно решать в первом приближении, когда [4]

(5)

Таким способом построения функций x(ξ) и y(h) является спо­соб, предложенный выдающимся советским ученым членом-корреспондентом АН СССР профессором В.З.Власовым. Суть способа состоит в построении аппроксимирующих функций, удовлетворяющих всем граничным условиям, а также и характеру внешней нагрузки.

Проиллюстрируем данный способ на конкретном примере, Предположим, что надо построить статическим методов Я.З.Власова аппроксимирующие функции х(ξ), у(h) для пластины, изображенной на рис. 3 и имеющей значение параметров μ=0.3 и γ=2.

Рис.3

На рис. 3 и в дальнейшем заменяем пластину ее срединной плоскостью [1+4], штриховкой обозначаем защемленный край пластины, на котором в ноль обращаются прогиб w(ξ,h) и угол поворота сечения w’_ξ(ξ,h) (или w’_h(ξ,h)). Пунктиром обозначаем шарнирно-опертый край, на котором в ноль обращается прогиб w(ξ,h) иизгибающий момент М_ξ(ξ,h) (или М_h(ξ,h)). Если край свободен от опорных закреплений, то их обозначения отсутствуют и на краю обращается в ноль изгибающий момент М_ξ(ξ,h) (или М_h(ξ,h)) ипри­веденная поперечная сила Q_ξ(ξ,h) (или Q_h(ξ,h)).

Строим статическим методом [1] аппроксимирующую функцию х(ξ).

Граничные условия по оси ξ в пластине следующие: при ξ=1- шарнирный край, т.е. w(0,h)=0 и М’_ξ(1,h)=0, при ξ=1 – защемление, т.е. w(1,h)=0 и w’_ξ(1,h)=0. Подставляя выражение (5) для w(ξ,h) в формулы для w, М_ξ, w’_ξ, получим

(6)

Преобразуя (6), получаем систему следующих четырех граничных условий

, , , . (7)

Отметим, что приведение условия М_ξ(0,h)=0 к условию возможно из-за выполнения условия - шарнирный край.

Рассмотрим вырезанную из пластины элементарную полоску шириной dh как обыкновенную балку и определим для этой балки в соответствии с граничными условиями линию прогибов от заданной нагрузки [1]. Балка изображена на рис.4, а нагрузка является равномерной, т.к. , т.е. , - см. рис.3.

Рис.4

Записываем в безразмерном виде дифференциальное уравнение изгиба балки

, (8)

где - характер изменения нагрузки по оси ξ.

Последовательно интегрируем (8) четыре раза:

(9)

(10)

(11)

. (12)

Произвольные постоянные интегрирования С₁, С₂, С₃, С₄ определяем из заданных граничных условий (7). Из условия получаем С₄=0, а из условия - C₂=0.

Для нахождения С₁ и С₂ используем оставшиеся условия , , приводящие к системе алгебраических уравнений:

(13)

Решая (13), находим величины С₁ и С₂

С₁= -3/8, С₃=1/48. (14)

Подставляя полученные значения С₁, С₂, С₃, С₄ в х(ξ) (13), получаем:

. (15)

Аппроксимирующая функция х(ξ) (15) соответствует граничным условиям в пластинке на сторонах контура ξ=0 и ξ=1 и характеру распределения нагрузки вдоль оси ξ.

Отметим следующее обстоятельство. Нас интересует характер прогиба пластины в направлении оси ξ- амплитуду В прогиба мы найдем в дальнейшем методом Бубнова – Галеркина. В связи с этим выражение (15) для х(ξ) желательно упростить так, чтобы коэффициент при старшей степени ξ был равен единице, т.е. принять

. (16)

Переходим к построению аппроксимирующей функции у(h). Граничные условия по оси h в пластине следующие: при h=0 – шарнирный край, т.е. w(ξ,0)=0, M_h(ξ,0)=0, при h=1- свободный край, т.е. М_h(ξ,1)=0, Q^*_h(ξ,1)=0. Подставляя выражение (5) для w(ξ,h) в формулы для w, М_h, w’_h, Q^*_h, получим

(17)

.

Условия (17) при h=0 можно привести к виду

, . (18)

Условия же при h=1 не допускают упрощения, т.к. при h=1 на свободном краю пластины у(1)≠0, у”(1)≠0, y’”(1)≠0.

Необходимо обратить внимание на то, что на шарнирном краю пластинки упрощаются, например, из (6) получено (7).

Таким образом, граничные условия по осиh имеют вид:

(19)

.

Отметим, что в граничные условия (19) вошла функция х(ξ) и ее производная х”(ξ), которые меняют свои значения вдоль оси ξ.

К связи с этим возникает необходимость заменить требование равенства нулю М_h и Q^*_h в любой точке края h=1 условиями равенства нулю суммы работ всех моментов М_h(ξ,1) на углах поворота w’_h (ξ,1) и приведенных поперечных сил Q_h(ξ,1) на прогибах w(ξ,1) вдоль края пластины h=1. Эта замена называется смягчением граничных условий. В силу принципа Сен - Венана [4] вносимая при смягчении граничных условий погрешность будет сказываться в малой зоне пластины у края h=1.

Таким образом, окончательно после их смягчения граничные условия по оси h принимают вид:

(20)

Вырезанная из пластинки элементарная полоска шириной представлена на рис.5.

Рис.5

Следует помнить, что граничные условия для данной балки- полоски отличаются от граничных условий (20) для пластины.

Поперечная нагрузка в пластине изменяется по оси h по линейному закону G(h)=h, поэтому дифференциальное уравнение изгиба рассматриваемой балки-полоски в безразмерном виде.

. (21)

Последовательно интегрируя (21) четыре раза:

(22)

(23)

(24)

. (25)

Произвольные постоянные интегрирования С₁, С₂, С₃, С₄ находим из граничных условий (20). Из условия получаем С₄=0, а из - С₂=0.

Для нахождения С₁ и С₂ используем два оставшихся уравнения системы (20). Берем х(ξ) в виде (16) и вычисляем входящие в (20) определенные интегралы:

Подставляя в (26) формулы (22) – (25) и решая полученную систему, находим С₁=-0.0980, С₃=0.0281.

Подставим полученные значения С₁, С₂, С₃, С₄ в у(h):

. (27)

Упрощаем выражение для у(h) так, чтобы коэффициент при h⁵ был равен 1, и получаем

. (28)

Аппроксимирующая функция у(h) (28) соответствует граничным условиям в пластине по оси h и характеру распределения поперечной нагрузки по этой оси.

Рассмотрим возможные пути построения аппроксимирующих функций статическим методом В.З. Власова для пластин, различным образом закрепленных по контуру – рис.6.

Рис.6

На рис. 6а изображена пластина, на сторонах контура которой или жёсткое защемление, или шарнирное опирание. Для таких типов закреплений аппроксимирующие функци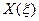и и 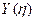строятся независимо одна от другой и без смягчения граничных условий.

На рис. 6б изображена пластина, у которой на сторонах контура и -заделка, на стороне контура -шарнирное опирание, а на стороне контура -свободный край. Сначала необходимо построить функцию 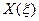, затем использовать её для нахождения функции 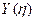, используя смягчённые на свободном краю пластин при условия и условия при .

(29)

Для изображённой на рис. 6в пластины сначала необходимо построить функция 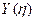, а затем найти функцию 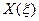, используя смягчённые на свободных краях пластины и условия

(30)

При построении аппроксимирующих функций следует обратить внимание на то, что степень полинома 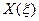(или 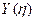) зависит от характера распределения нагрузки по ос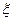и или 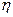. Если распределение равномерное, то полином (например, (16)) имеет порядок 4, если линейное, то (например, (28))-порядок 5, а при распределении поперечной нагрузки по квадратичной параболе порядок полинома составляет 6.