Устойчивость откоса грунта, обладающего трением и сцеплением
Определение напряжений в массиве грунта от сосредоточенной силы. Задача Буссинеску 1885 г.
Составим расчётную схему данной задачи, представив грунтовое основание, как упругое полупространство.
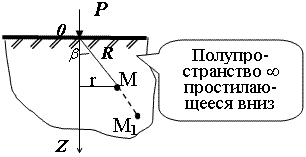
Графическое представление условий (расчётная схема) задачи для определения напряжений в массиве грунта от сосредоточенной силы.
По условиям задачи необходимо определить значения вертикальных напряженийσz и касательных напряженийτzx;τzy в точке М, расположенной на площадке, параллельной плоскости, ограничивающей массив от действия сосредоточенной силы Р.
Решим эту задачу в три этапа:
1. Определим σR – в радиальном направлении перпендикулярно R (в т. М)
2. Определим σR' – в радиальном направлении (приложенном к площадке, параллельной плоскости ограничивающей массив).
3. Определим σz;τzx;τzy.
1 этап решения задачи:
Допустим, что под действием силы Р точка М переместилась в точку М1. Обозначим S – перемещение точки М. Тогда можно записать:
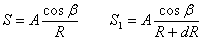
Мы получили перемещение точки М (см. выше приведённый рисунок).
В представленной зависимости осадка точки будет прямо пропорционально завесить от косинуса угла β и обратно пропорционально радиусу расположения точки, где А – коэффициент пропорциональности.
Определим относительное перемещение точки:
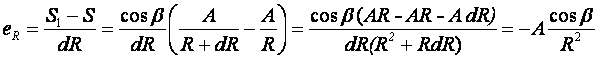
Согласно первому постулату теории упругости между напряжениями и деформациями должна быть прямая зависимость, следовательно:
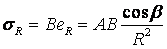
Радиальное напряжение в точке М.
В этой формуле В – коэффициент пропорциональности. Для определения σR необходимо определить произведение коэффициентов АВ.
σR – определяется по методу, используемому в сопромате («метод сечений»: мысленно разрезают балку, одну часть отбрасывают и оставшуюся часть уравновешивают).
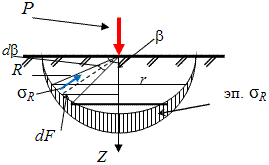
Расчётная схема для определения радиальных напряжений в грунте.
Для решения данной задачи поступим аналогичным образом. Рассматрим полушаровое сечение радиусом R и заменим отброшенное пространство напряжениями σR. Рассмотрим изменение β в пределах dβ. Составим уравнение равновесия на ось Z:
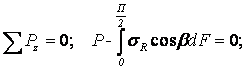
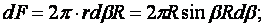
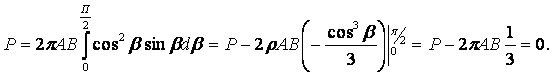
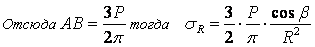
Величина радиального напряжения в грунте зависит от координат точки и величины прикладываемой силы.
2 этап решения задачи:
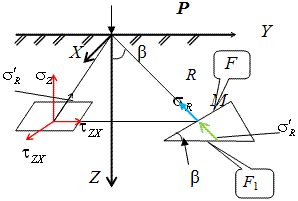
Схема пересчёта радиальных напряжений к вертикальным.
Из геометрических соотношений можно записать:
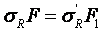
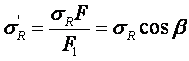
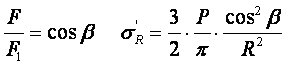

Мы получили величину радиальных напряжений, приложенных к площадке параллельно плоскости, ограничивающей массив.
3 этап решения задачи:
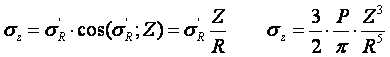
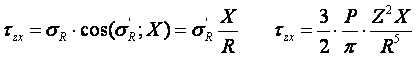
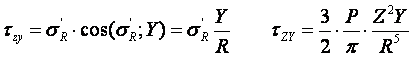
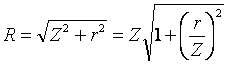 , подставим и получим
, подставим и получим
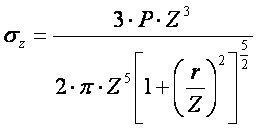
Введём обозначение:
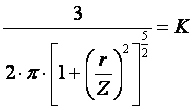
Упрощая выше полученное выражение, вводим значение коэффициента К. Тогда получим:
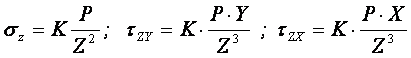
Результат окончательного решения нашей задачи.
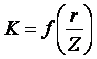 – определяется по таблице.
– определяется по таблице.
Определение напряжений sz в массиве грунта от действия нескольких сосредоточенных сил (принцип Сен-Венана – принцип независимости действия сил)
Пусть к поверхности грунта приложены несколько сосредоточенных сил разной интенсивности.
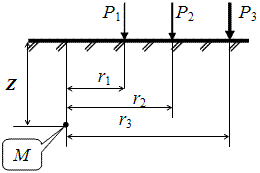
Расчётная схема для определения напряжений в точке М от действия нескольких сосредоточенных сил.
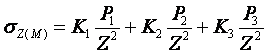
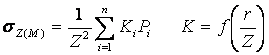
Используя принцип независимости действия сил, легко определить напряжения в любой точке М, расположенной на любой глубине.
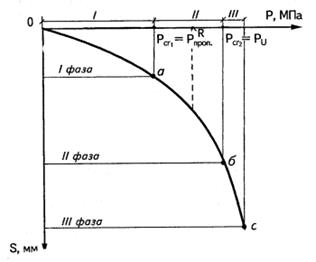
16.Фазы напряженного состояния грунта
При возведении здания или сооружения наблюдается постоянное возрастание давления по подошве фундаментов. При таком характере воздействия в грунтовом основании, как и во всяком твердом теле, возникает напряженно-деформирующее состояние (НДС), которое адекватно интенсивности приложенной внешней нагрузки, причем возникает оно не только в точках контакта подошвы фундамента сооружения и грунта основания, но и на значительной глубине.
Распределение напряжений как под подошвой фундамента, так и на значительной глубине необходимо знать, так как прочность и устойчивость сооружений зависит от сопротивления (R) грунта, не только примыкающей к подошве, но и глубоколежащего.
При деформации грунтов под нагрузкой Н.М. Герсеванов выделил три фазы НДС:
I — фаза нормального уплотнения;
II — фаза сдвигов;
III — фаза выпирания грунта.
Зависимость вертикальных перемещений фундамента от действующего давления по его подошве изображена на рис. 6.5.
18. Метод Н.Н Маслова построения равнопрочного откоса.
Построение равнопрочного откоса (метод Н.Н. Маслова)
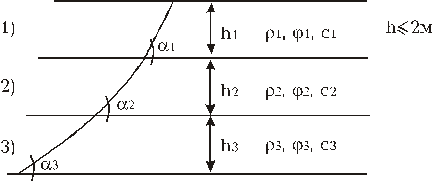
h £ 2м
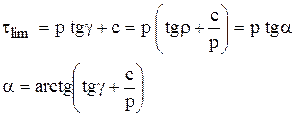
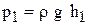
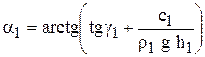
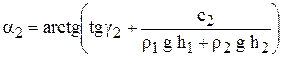 (a2 < a1)
(a2 < a1)
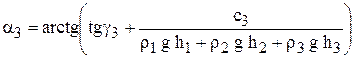 (a3 < a2)
(a3 < a2)
Практически: a < g, поэтому вводится коэф-т запаса (устойчивости) kst.
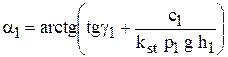
kst = 1,1…1,2
19. Оценка устойчивости откоса методом КЦПС.
Широко применяется на практике, т.к. дает некоторый запас устойчивости и основывается на опытных данных о форме поверхностей скольжения при оползнях вращения, которые принимают за круглоцилиндрические. Самое их невыгодное положение определяется расчетом. Это приблизительный метод. Задается центром вращения «О» откоса «АВ». Проводим след круглоцилиндрической поверхности радиусом «R» через т. А. Призму обрушения «АВС» делим вертикальными плоскостями на «n» отсеков. Каждый отсек – твердое тело, сползающее по наклонной поверхности (упрощают: дугу заменяют хордой). Суммируют силу тяжести каждого отсека с его внешней нагрузкой и сносят равнодейств. на поверхность скольжения.
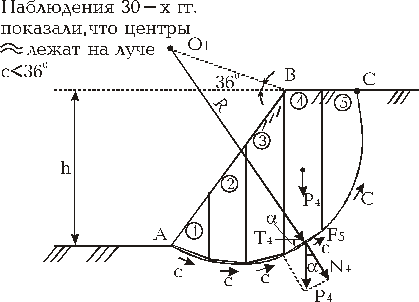
Уравнение равновесия
S Мо = 0
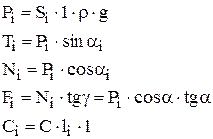
где Ti – тангенциальная (касательная )составляющая силы тяжести
Ni – нормальная составляющая
Fi – сила трения
Ci – сила сцепления
C – удельное сцепление
21. Предельное состояние сыпучего грунта в точке. (30)

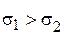 плоская задача, рассматриваются главные напряжения.
плоская задача, рассматриваются главные напряжения.
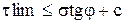 - условие предельного равновесия.
- условие предельного равновесия.
А – центр круга Мора; В – точка касания; С – диаграмма Кулона; Д – касание Д. К. с осью х.
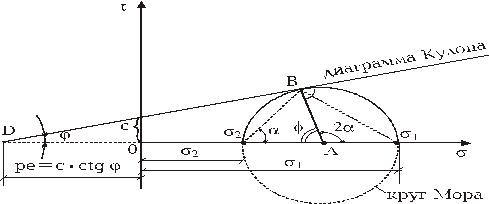
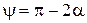
Из 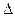 АВD:
АВD: 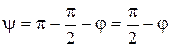 ;
; 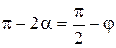 ;
; 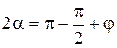
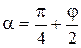 - направление площадок скольжения.
- направление площадок скольжения.
Значение напряжений на предельной прямой (д. Кулона) отвечает точке В, которая одновременно принадлежит кругу предельных напряжений Мора (ДВ – касательная к кругу, ДВ (АВ) и проходит через начало координат (здесь точка 2). В условиях предельного равновесия площадки скольжения наклонены под углом 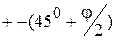 к направлению площадки наибольшего главного направления, или <
к направлению площадки наибольшего главного направления, или < 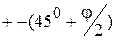 к направлению главного напряжения
к направлению главного напряжения 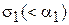 . Для связных грунтов (рассматриваем
. Для связных грунтов (рассматриваем 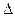 АВД):
АВД):
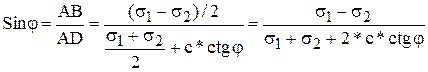
Для сыпучих грунтов (с=0), несвязных:
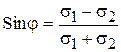 - это условие прочности Рэнкина.
- это условие прочности Рэнкина.
(математическое выражение условия предельного равновесия (условие прочности Мора) сыпучих и связных грунтов).
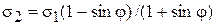 , или
, или 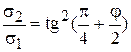 - сыпучие грунты, условие предельного равновесия.
- сыпучие грунты, условие предельного равновесия.
В скобках знак «-» - активное давление; «+» - пассивное сопротивление сыпучих грунтов.
22. Предельное состояние связного грунта в точке.
Для связных грунтов условие предельного равновесия:

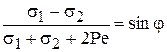 ;
; 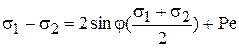 ; т.к.
; т.к. 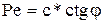
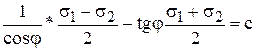
При давлениях на грунт, больших структурной прочности установлены две критические нагрузки:
1) нагрузка, сооветствующая началу возникновения в грунте зон сдвигов и окончанию фазы уплотнения  предельное напряженное состояние – начальная критическая нагрузка безопасная в основаниях сооружений, т.к. до ее достижения грунт в фазе уплотнения.
предельное напряженное состояние – начальная критическая нагрузка безопасная в основаниях сооружений, т.к. до ее достижения грунт в фазе уплотнения.
2) нагрузка, при которой формируются сплошные области предельного равновесия, грунт неустойчив (исчерпание его несущей способности – предельная критическая нагрузка на грунт в данных условиях.
23.Начальное критическое давление фундамента на основание.
Определение начального критического давления на грунтовое основание
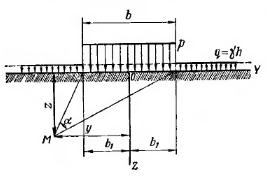
Начальным критическим давлением на основание называется то значение давления, при котором в грунте основания возникают области предельного напряженного состояния. При давлениях меньших начальных критических значений во всех точках основания (рис. 6.5) напряженные состояния допредельные, что совершенно безопасно для оснований сооружений. В этом случае до достижения начального критического давления грунт находится в фазе уплотнения (см. рис. 6.6) и подход к ее определению демонстрируется для полосовой нагрузки на грунт. На рис. 8.5 представлены ее реальная и расчетные схемы.
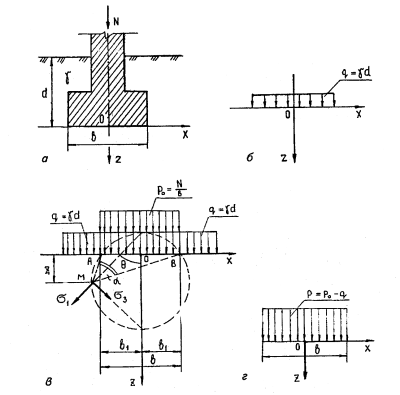
Рис. 8.5. Реальная (а) и расчетные (б, в, г) схемы к определению начального критического давления
Для нахождения начального критического давления значения главных напряжений σ1 и σ3 определяются с учетом приложенной нагрузки Р = Р0— q и соответственно веса грунта.
Вертикальное сжимающее напряжение (давление) от собственного веса грунта в точке М (см. рис. 8.5,в), лежащей на глубине z от подошвы фундамента, определяется из выражения
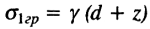 (8.18)
(8.18)
Полные главные напряжения в грунте на глубине :
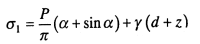 (8.19)
(8.19)
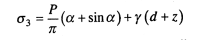 (8.20)
(8.20)
На площадках сдвига, когда грунт от действия нагрузки находится в конце среза уплотнения, имеет место предельное равновесие:
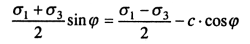 (8.21)
(8.21)
Тогда, подставив (8.19) и (8.20) в (8.21), получим уравнение кривой, соответствующей границе пластической зоны грунта:
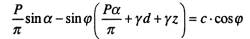 (8.22)
(8.22)
Выражение (8.22) можно рассматривать как уравнение границы области, проходящей через точку М (см. рис. 8.5,в), на контуре которой при действии под подошвой фундамента давления Р имеет место состояние предельного равновесия. Координаты точек этой границы определяются неизвестными z и α.
Решая уравнение (8.22) относительно z, получим:
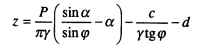 (8.23)
(8.23)
Приравняв первую производную этого выражения по α нулю, находим максимальную глубину границы этой области zmax, где площадка скольжения получает опасный наклон к горизонту:
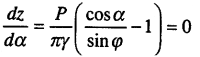 (8.24)
(8.24)
Из уравнения (8.24) следует, что при z = zmax, cosα = sinφ или α = π/2-φ
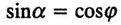 (8.25)
(8.25)
Тогда, подставляя (8.25) в формулу (8.24), получаем выражение для низкой точки сдвига грунта (zmax) в следующем виде:
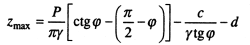
(23)24.Предельное критическое давление на основание.
Две критические нагрузки: 1 — нагрузка, соответствующая началу возникновения в грунте зон сдвигов и окончанию фазы уплотнения, когда под краем нагрузки между касательными и нормальными напряжениями возникают соотношения, приводящие грунт (сначала у ребер подошвы фундаментов) в пре-
дельное напряженное состояние, и 2 — нагрузка, при которой под
загруженной поверхностью сформировываются сплошные области
предельного равновесия, грунт приходит в неустойчивое состояние
и полностью исчерпывается его несущая способность.
Величину первой нагрузки назовем начальной критической нагрузкой начРкр, еще совершенно безопасной в основаниях сооружений, так как до ее достижения грунт всегда будет находиться в фазе уплотнения, а вторую, при которой исчерпывается полностью несущая способность грунта,— предельной критической нагрузкойна грунт в данных условиях загружения.
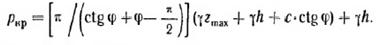
Если совершенно не допускать ни в одной точке развития зон предельного равновесия под подошвой фундаментов, то следует положить в уравнении 
Называя наибольшее давление, при котором ни в одной точке грунта не будет зон предельного равновесия (Zmax=0),начальным критическим давлением на грунт нач Pкрит :
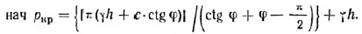
Предельная нагрузка, соответствующая полному исчерпанию несущей способности грунта и сплошному развитию зон предельного равновесия, что достигается для оснований фундаментов при окончании формирования жесткого ядра, деформирующего основание и распирающего грунт в стороны.
Впервые эта задача для невесомого грунта, нагруженного полосообразной нагрузкой (предельная величина которой определяется), была решена Прандтлем и Рейснером (1920—1921), причем для предельной нагрузки на грунт получено следующее выражение:
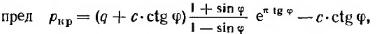
где q - боковая пригрузка, равная yh (h-глубина приложения полосообразной нагрузки.)
26. Устойчивость откоса связного грунта.
Устойчивость откоса грунта, обладающего трением и сцеплением
Условию заголовка соответствуют глинистые (связные) грунты (супеси, суглинки), для которых φ ≠ 0; С ≠ 0 (Используем графо - аналитический метод расчета).
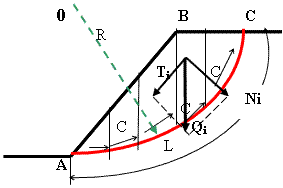
Расчётная схема для определения устойчивости откоса связного грунта.
Для решения данной задачи примем допущение, что обрушение откоса может происходить по кругло цилиндрической поверхности АС с радиусом R, относительно центра вращения т. O (см.расчётную схему на рисунке).
Как рассчитать устойчивость такого откоса?
ηуст. – коэффициент устойчивости откоса может быть определен отношением момента удерживающих сил к моменту сдвигающих сил:
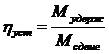
Порядок вычислений принимаем следующий (см. приведенную схему):
1. Откос АВС делим на ряд призм вертикальными плоскостями.
2. Определяем вес каждой из призмы – Qi.
3. Раскладываем Qi на Ti и Ni.
4. Находим величину сцепления (с) по основанию каждой призмы и L – длину дуги.
Определим момент удерживающих сил 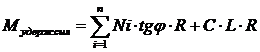
Определим момент сдвигающих сил 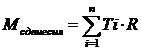 , где n - число призм.
, где n - число призм.
Отсюда находим ηуст.
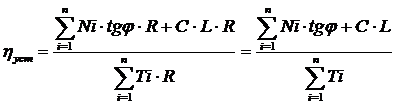
Выражение для определения коэффициента устойчивости связного грунта.
Недостаток этого метода – это произвольное построение поверхности обрушения. (Точкой O мы задались произвольно). Необходимо найти наиболее опасный центр вращения, с ηуст.= min, т.е. наиболее вероятную поверхность обрушения.
25.Устойчивость откоса идеального сыпучего грунта.
Идеально сыпучее тело характеризуется отсутствием сцепления (с=0). Рассмотримоткос с углом заложения α и углом внутреннего трения φ песка, слагающего откос:
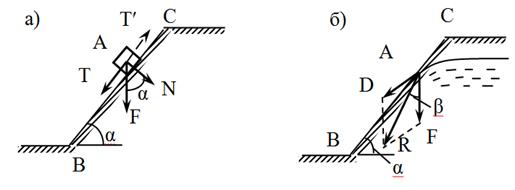 Рис 1.
Рис 1.
Исследуем условия равновесия частицы грунта А, свободно лежащей на поверхности откоса.Вес частицы F разложим на нормальную N и касательную составляющую Т, стремящуюся сдвинуть частицу вниз. Грунт обладает только внутренним трением, поэтому устойчивость (неподвижность) частицы будет обеспечена, покасдвигающая сила Т будет равна удерживающей силе трения Т′=f∙Nилименьше ее.
Учитывая, чтоN=F∙cosα,T=F∙sinα, из уравнения проекций на наклонную грань следует:
F∙sinα=f∙Fcosα,откуда tgα=f. Но коэффициент трения f=tgφ. Значитα=φ, то естьпредельный угол откоса сыпучих грунтов равен углу внутреннего трения, отождествляемому часто с углом естественного откоса.
Для обеспечения устойчивости откоса сила, удерживающая частицы А, должна быть больше сдвигающих сил: Т≤Т′.
Если обозначить коэффициент надежности γn, тогда это условие примет вид:
γntgα≤ tgφ. Обычно принимаютγn=1,1÷1,2.
Если уровень подземных вод в массиве сыпучего грунта находится выше подошвы откоса, возникает фильтрационный поток, выходящий на поверхность откоса. В грунте возникаетгидродинамическое давление, что приводитк уменьшению устойчивостиоткоса (рис.1, б). Поэтому, рассматривая равновесие частицы А на поверхности откоса,к сдвигающей силе необходимо добавить гидродинамическую составляющую D=γв∙n∙i, где:
γв– удельный вес воды,
n – пористость грунта,
i – градиент напора.
В точкевыхода воды через поверхность откоса действуют силы D и F, которые приводят к равнодействующей R. Эта сила отклонена от вертикали на угол β. В этом случае условие устойчивости откоса примет вид:
γntgα≤ tg (φ- β)
