Определение коэффициента самоиндукции катушки

Оборудование: исследуемая катушка, сердечник, вольтметр, амперметр, источник переменного тока (регулятор напряжения школьный РНШ).

1.Теоретическое введение

Если в проводнике изменяется сила тока, то в нем возникает электродвижущая сила ЭДС самоиндукции, препятствующая этому изменению. ЭДС самоиндукции пропорциональна изменению тока в единицу времени:

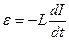(1)

где L - коэффициент пропорциональности называемый коэффициентом самоиндукции или индуктивностью проводника.

Индуктивность проводника зависит от формы и размеров проводника, от магнитной проницаемости окружающей среды. Если e = 1В, скорость изменения тока dI/dt = 1А/с, то L = 1 Гн (Генри). Иначе говоря, индуктивностью в 1 Гн обладает такой проводник, в котором изменение тока со скоростью 1 А в 1с вызывает ЭДС самоиндукции в 1В. У линейных проводников коэффициент самоиндукции мал. Большими коэффициентами самоиндукции обладают так называемые катушки индуктивности, состоящие из большого числа витков.

Пусть сопротивление постоянному току проволоки, из которой намотана катушка, равно R. Это сопротивление называется чисто активным или омическим. На активном сопротивлении электромагнитная энергия преобразуется во внутреннюю энергию, в результате чего происходит нагревание проводника. Если включить катушку в цепь переменного тока, то вследствие периодического изменения силы тока возникает ЭДС индукции, которая в соответствии с законом Ленца противодействует изменениям силы тока в цепи. Это приводит к уменьшению амплитуды переменного тока и, следовательно, к тому, что сопротивление катушки становится больше чем активное. Иначе говоря, катушка индуктивности будет обладать не только активным, но и индуктивным сопротивлением R_L. Индуктивное сопротивление R_L = wL, где w = 2pn - круговая частота или циклическая, n - частота переменного тока ( n = 50 Гц).

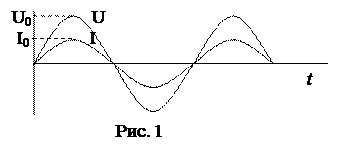Если в цепь переменного тока включен конденсатор емкостью С, то вследствие периодического изменения переменного тока происходит его перезарядка, что приводит к появлению емкостного (реактивного) сопротивления R_C = 1/wС.

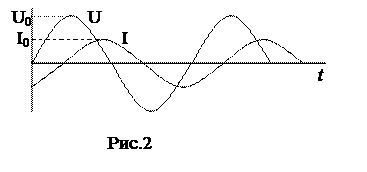На активном сопротивлении колебания тока и напряжения совпадают по фазе (рис. 1)

U = U_оsin wt

I = I_оsin wt

Если цепь обладает чисто индуктивным сопротивлением, то колебания тока и напряжения сдвинуты по фазе на p/2 , причем колебания напряжения опережают колебания тока (рис. 2). Действительно, при включении катушки в цепь на ее концах сразу устанавливается напряжение источника. Ток же, вследствие явления самоиндукции, нарастает постепенно и отстает от напряжения на катушке.

U = U_оsin wt

I = I_оsin(wt - p /2)

В цепи, обладающей только емкостным сопротивлением, колебания тока и напряжения тоже сдвинуты по фазе на p/2 , но при этом колебания тока опережают колебания напряжения (рис. 3). Физический смысл этого явления в том, что напряжение на конденсаторе определяется имеющимся на нем электрическом заряде. Но этот заряд образован током, протекающим в более ранней стадии колебательного процесса. Поэтому колебания напряжения запаздывают относительно колебаний тока.

U = U_оsin wt

I = I_оsin(wt + p/2)

Рассмотрим цепь, состоящую из последовательно соединенных сопротивления R, индуктивности L, конденсатора С (рис. 4). Известно, что в цепи постоянного тока при последовательном соединении полное напряжение равно алгебраической сумме напряжений на участках цепи

U = U₁ + U₂ + U₃

и полное сопротивление

R = U/I = R₁ + R₂ + R₃

Не так обстоит дело в цепи переменного тока. Амплитуды и фазы тока в любой момент времени одинаковы на активном, индуктивном и емкостном сопротивлениях рассматриваемой цепи I = I_о×sinwt. Однако, на активном сопротивлении напряжение совпадает по фазе с током U_R = I_OR×sinwt, на индуктивном напряжение опережает ток 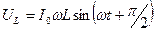, на емкости отстает от тока 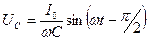. Значит, складывать приходится колебания напряжения различные по фазе. В результате полное сопротивление при переменном токе не равно сумме активных и реактивных сопротивлений. Если учесть сдвиг фаз между напряжениями, то полное сопротивление Z цепи, изображенной на рис. 4, равно:

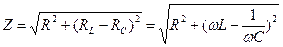(1)

Несовпадение колебаний тока и напряжения по фазе приводит к тому, что закон Ома (в том виде, как он был сформулирован для постоянного тока) несправедлив для мгновенных значений тока и напряжения. Но, однако, он справедлив для амплитудных значений I_о и U_о.

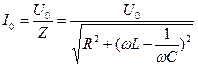(2)

закон Ома для переменного тока

Электроизмерительные приборы (амперметры, вольтметры) показывают не максимальные значения тока и напряжения, а эффективные или действующие. Между эффективными и максимальными значениями тока и напряжения существуют соотношения:

.

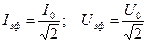Закон Ома для переменного тока справедлив и для эффективных значений тока и напряжения.

Любая катушка обладает активным сопротивлением R_R и индуктивным R_L (R_C® 0), поэтому полное сопротивление катушки:

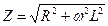, откуда 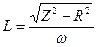(3)

Следовательно, для определения коэффициента самоиндукции катушки необходимо знать полное сопротивление Z, омическое (активное) сопротивление R и круговую частоту w = 2pn.

2.Описание лабораторной установки и метода измерения

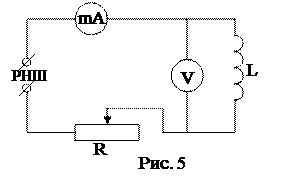
Лабораторная установка собирается по схеме изображенной на рисунке 5.

Здесь:

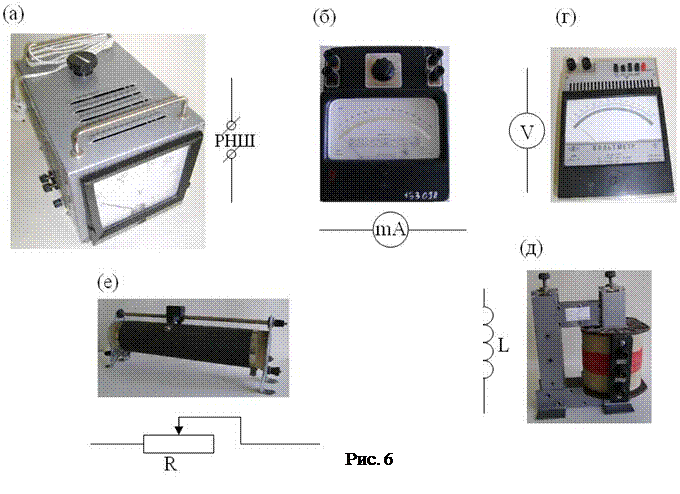
РНШ – источник переменного тока с частотой n=50 Гц (рис. 6 а);

mA – миллиамперметр (рис. 6 б);

V – вольтметр (рис. 6 г);

L – катушка индуктивности (рис. 6 д);

R – реостат (рис. 6 е).

3.Порядок выполнения работы и обработка результатов

Задание 1. Изучение зависимости коэффициента самоиндукции от числа витков катушки

1. Включить регулятор напряжения РНШ в сеть и установить движок на "0".

2. Выключить РНШ из сети, собрать цепь по рис. 5.

РНШ - источник переменного тока с частотой 50 Гц.

3. Катушку подключить на 1200 витков. Установить движок РНШ на определенное напряжение и измерить силу тока I_эф и напряжение U_эф на катушке по вольтметру. Результаты занести в таблицу. Повторить измерения при различных напряжениях.

4. Подсчитать 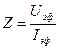, коэффициент самоиндукции L (по формуле 3). Найти среднее значение L_ср и погрешность.

ВНИМАНИЕ!!! Все переключения в цепи производить только после предварительной установки движка РНШ на "0" и, ВЫКЛЮЧИВ РНШ из сети.

5. Включив в цепь катушку на 2400 витков, измерить U_эф и I_эф, вычислить Z и L.

6. Повторить опыт с катушкой на 3600 витков. Результаты занести в таблицу1.

Таблица 1

Число витков	№	R, Ом	IЭФ, А	UЭФ , В	Z , Ом	L , Гн	LСР, Гн	DL, Гн	DLСР , Гн	e %
С замкнутым сердечником

Задание 2. Изучение зависимости коэффициента самоиндукции от сердечника

1. Повторить опыт, используя катушку на 1200, 2400 и 3600 витков с разомкнутым железным сердечником. Результаты занести в таблицу 2.

2. Установить, как меняется индуктивность L от наличия сердечника.

3. Сделайте выводы по работе.

Таблица 2

Число витков	№	R, Ом	IЭФ, А	UЭФ , В	Z , Ом	L , Гн	LСР, Гн	DL, Гн	DLСР , Гн	e %
С разомкнутым сердечником

ВОПРОСЫ:

1. Что называется индуктивностью проводника? Единицы измерения.

2. Почему катушка оказывает разное сопротивление постоянному току и переменному?

3. От чего зависит индуктивное сопротивление катушки?

4. Как связаны индуктивное и активное сопротивление проводника? Можно ли их просто складывать?

5. Что означает, что ток по фазе не совпадает с напряжением?

6. Когда в цепи переменного тока, напряжение и ток совпадают по фазе?

7. Что такое емкостное сопротивление? Чем оно обусловлено? Как оно влияет на ток в цепи?

8. Как увеличить индуктивность катушки?

9. Как регулируется напряжение в цепи?

Литература:

1. Савельев И.В.. Курс общей физики. Т.2. М. Наука. Физматлит. 1998 г. (Издание 4-ое переработанное). С.5-206.

2. Трофимова, Т. И.Курс физики : Учеб. пособие для вузов / Т. И. Трофимова. - 7-е изд., стер. - М. : Высш. шк., 2003. - 542 с. - Рек. Мин. обр. РФ. - ISBN 5-06-003634-0.

3. Шубин. А.С. Курс общей физики. - М.: Высш. Школа, 1976.

Содержание

Числовая обработка результатов лабораторного эксперимента.. 2

ОПРЕДЕЛЕНИЕ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ СРЕДЫ (Лаб.№1) 4

ОПРЕДЕЛЕНИЕ ЕМКОСТИ КОНДЕНСАТОРОВ (Лаб.№2) 8

Измерение сопротивлений с помощью моста Уитстона (Лаб.№3) 12

ИЗУЧЕНИЕ ЗАВИСИМОСТИ СОПРОТИВЛЕНИЯ ПРОВОДНИКОВ ОТ ТЕМПЕРАТУРЫ (Лаб.№4) 16

СНЯТИЕ ХАРАКТЕРИСТИКИ ПОЛУПРОВОДНИКОВОГО ДИОДА (Лаб.№5) 19

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА САМОИНДУКЦИИ КАТУШКИ (Лаб.№6) 22

Литература: 27