Построение и исследование регрессионных моделей

Зависимость между случайными величинами называется регрессией. Она понимается как зависимость между математическими ожиданиями этих величин.

Форма связи между случайными величинами определяется линией регрессии, показывающей, как в среднем изменяется величина Y при изменении величины Х, что характеризуют условным математическим ожиданием m_y/x величины Y, вычисляемым при Х = х. Таким образом, кривая регрессии Y на Х есть зависимость условного математического ожидания Y от известного значения Х.

Математическая постановка задачи регрессионного анализа:

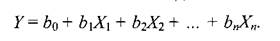для каждого i-го опыта имеется набор значений входных параметров X_1i, X_2i, …, X_ni и соответствующее этому набору значение выходного параметра Y_i. Необходимо определить зависимость выходного параметра Y от входных факторов X_1i, X_2i, …, X_ni, которая в случае, например, линейной связи может иметь вид

Такая зависимость называется линейной регрессией. Любая другая зависимость называется нелинейной регрессией.

Задача сводится к тому, чтобы при измеренных во время опытов значениях входных переменных X₁, X₂, …, X_n и выходной переменной Y найти коэффициенты уравнения регрессии b₀, b₁, b₂, …, b_n, которые с определенной вероятностью будут отражать связь аргументов X₁, X₂, …, X_n с Y.

Регрессионная зависимость вида Y = f(X_i) называется однофакторной или парной и описывает связь между двумя переменными: входной Х и выходной Y.

Регрессионная зависимость вида Y = f(X₁, X₂,…, X_n) называется многофакторной или множественной и описывает связь между несколькими входными X₁, X₂, …, X_n и одной выходной переменной Y.

Построение и исследование регрессионной модели можно разбить на четыре этапа.

1-й этап. Проверка наличия стохастической связи между исследуемыми величинами. Для этого нужно определить по значению r_xy, существует ли корреляционная связь между Х и Y.

2-й этап. Выбор вида уравнения регрессии. Вид уравнения регрессии выбирается исходя из особенностей изучаемой системы случайных величин. Один из возможных подходов при этом – экспериментальный подбор типа уравнения регрессии по соответствующим критериям адекватности. В случае же, когда имеется определенная априорная (доопытная) информация об объекте, более эффективным является использование для этой цели теоретических представлений о процессах и типах связей между изучаемыми параметрами.

3-й этап. Расчет параметров (коэффициентов) уравнения регрессии. Для определения параметров (коэффициентов) уравнения регрессии используется метод наименьших квадратов (МНК). Сущность метода заключается в том, что выбирается такая линия регрессии, при которой сумма квадратов разностей между экспериментальными значениями выходной переменной Y_i, 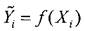полученными на объекте, и значениями, рассчитанными по выбранной регрессионной формуле (модели) ,будет минимальной:

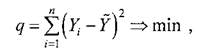
где q – критерий близости модели и объекта, называемый невязкой модели; n

– количество экспериментальных данных.

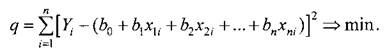Задача построения линейной модели сводится к минимизации функции невязки следующего вида:

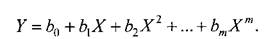В качестве нелинейных регрессионных моделей чаще всего используются полиномы разной степени:

4-й этап. Проверка адекватности структуры модели. Об адекватности структуры модели можно судить по коэффициенту корреляции r или корреляционному отношению η, гистограмме распределения остатков и содержательному анализу остатков модели.

Коэффициент корреляции r характеризует степень тесноты линейной

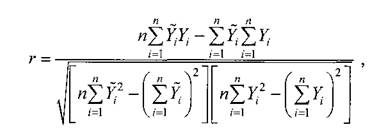связи между Y~ и Y. Приближенное значение r определяется по формуле

Коэффициент корреляции изменяется от –1 до +1.

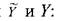
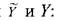Корреляционное отношение η характеризует степень тесноты нелинейной связи между переменными

Корреляционное отношение изменяется от 0 до 1.

Следует иметь в виду, что коэффициент корреляции является частным случаем корреляционного отношения и используется обычно только при исследовании линейных моделей.

Выводы о степени адекватности модели делаются на основании значения коэффициента корреляции или корреляционного отношения, которые должны быть близки к 1.

Другим критерием адекватности модели является содержательный анализ остатков модели. Он заключается в построении распределения остатков модели в зависимости от входного параметра X. Если закон распределения остатков близок к нормальному закону с математическим ожиданием, равным 0, то модель считается адекватной экспериментальным данным. этом случае гистограмма распределения остатков приобретает колоколообразный вид (см. рис. 4.1). При неадекватности модели она имеет несимметричный характер или второй горб.