Дать определение управляемости системы по критерию Гильберта

Управляемость и наблюдаемость линейных систем в MATHCAD

Исполнители, студенты группы 5Б13 Опарин А.О. ________

Щеголихин Д.С ________

Руководитель Кац М.Д. ________

подпись

Томск – 2013

Цель лабораторной работы заключается в освоении управляемости и наблюдаемости линейных систем в вычислительной системе Mathcad.

Задачами лабораторной работыявляются:

- освоение методики расчета управляемости и наблюдаемости систем по критерию Гильберта;

- освоение методики расчета управляемости и наблюдаемости систем по критерию Калмана.

Критерий Гильберта управляемости и наблюдаемости систем

Пример 1

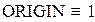
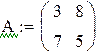
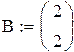
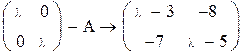
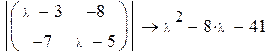
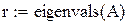
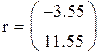
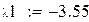
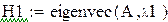
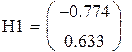
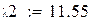
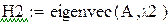
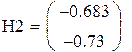
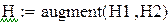
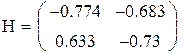
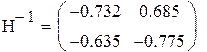
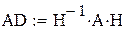
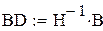
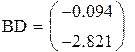
Так как на состояние v1 и v2 не влияет входной сигнал управления, система не управляема

Расчет наблюдаемости системы по Критерию Гильберта

Пример 2

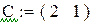
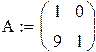
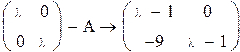
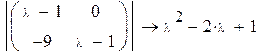
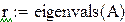
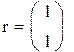
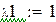
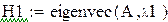
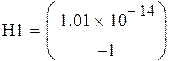
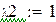
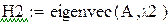
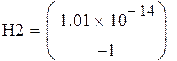
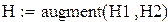
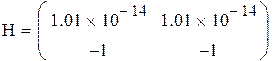
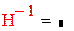
Так как определитель матрицы равен 0, обратной матрицы не существует.

Критерий управляемости и наблюдаемости системы Р. Е. Калмана

Пример 1

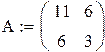
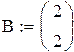
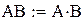
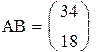
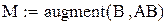
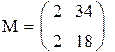
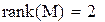
Так как ранг матрицы M равен порядку уравнения, система управляема.

Критерий управляемости и наблюдаемости системы Р. Е. Калмана

Пример 2

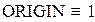
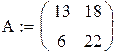
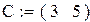
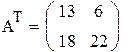
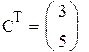
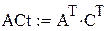
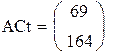
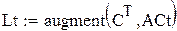
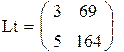
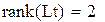
так как ранг матрицы L равен порядку уравнения, система наблюдаема.

Ответы на контрольные вопросы.

Дать определение управляемости системы по критерию Калмана.

Система полностью управляема, если n независимых скалярных уравнений удовлетворяют матричному уравнению.

Иначе говоря, система полностью управляема, если матрица имеет ранг n, где n - порядок системы.

2. Почему в функции ORIGIN следует поменять значение с нуля на единицу?

Индексация элементов матрицы задается значением системной переменной ORIGIN, которая по умолчанию равна 0.V0 - первый элемент вектора, M0,0 - первый элемент матрицы.

На рис.1 показано изменение индексации при различных значениях переменной ORIGIN (Набирается обязательно заглавными буквами).

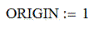
Методы введения элементов матрицы

Ввод элементов матрицы.

1 способ: Ввод в виде элементов массива.

1. В окне редактора устанавливаем курсор и щёлкаем левой кнопкой мыши. Появляется красный крестик.

2. При помощи клавиатуры набираем имя матрицы.

3. Набираем подстрочный индекс матрицы.

4. После этого ставим знак присваивания.

5. Набираем численные значения элемента.

2 способ: Использование шаблона матрицы.

1. В окне редактора набираем имя матрицы и ставим знак присваивания.

2. На панели инструментов находим кнопку: «Vector And Matrix Toolbar».

3. В появившемся меню нажимаем изображение шаблона матрицы.

4. В диалоговом окне указываем число строк и столбцов и нажимаем кнопку ОК.

5. Появляется шаблон матрицы, который сами заполняем нужными элементами.

Дать определение управляемости системы по критерию Гильберта

Система будет управляемой, если все переменные V*(t) не содержат свободных (неуправляемых компонентов).

Условием полной управляемости системы является отсутствие нулевой строки в матрице В*, т. е. все строки b[i] должны быть ненулевыми векторами- строками.