Пример расчета переходного процесса
В электрической цепи синусоидального тока методом отделения
Принужденной составляющей от свободной
Пусть в схеме на рис. 6.4 требуется определить  , если
, если 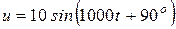 В,
В, 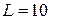 мГн,
мГн, 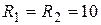 Ом.
Ом.
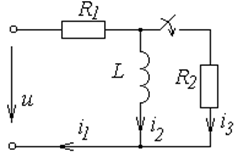
Рис. 6.4. Схема к примеру расчета
методом отделения принужденного режима от свободного
Анализируя докоммутационный режим, получаем
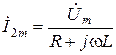 =
= 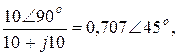
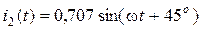 .
.
Тогда 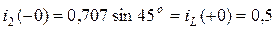 А.
А.
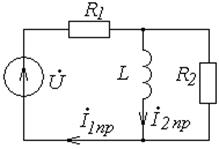 Рис. 6.5. Схема для расчета принужденного режима Рис. 6.5. Схема для расчета принужденного режима | 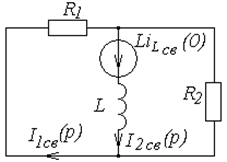 Рис. 6.6. Схема для расчета свободного режима Рис. 6.6. Схема для расчета свободного режима |
Определяем значение 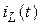 в принужденном режиме:
в принужденном режиме:
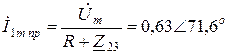 ,
,
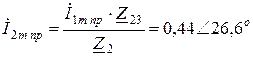 ,
,
где 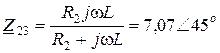 ;
;
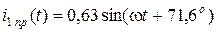 , А;
, А;
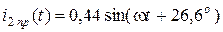 ;
;
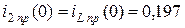 А.
А.
Свободную составляющую тока 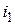 определим операторным методом.
определим операторным методом.
Эквивалентная операторная схема для свободного режима показана на рис. 6.6.
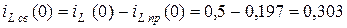 А.
А.
Так как 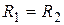 , то
, то
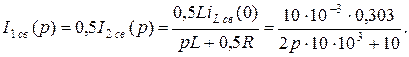
По теореме разложения 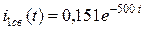 .
.
Окончательно 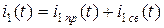 =
= 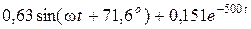 .
.
З а д а ч а 6. 1
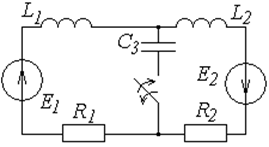
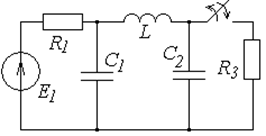
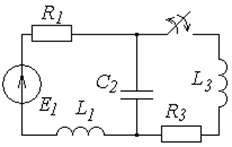
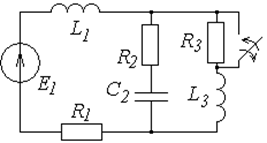
Постройте операторную схему замещения цепи, эквивалентная схема которой задана в табл. 6.1. Для вариантов 1 ¸ 15 ключ работает на включение, для вариантов 16 ¸ 30 – на отключение.
З а д а ч а 6. 2
Для схемы, соответствующей номеру варианта (табл. 6.3), определите операторным методом свободную составляющую искомой функции, указанной в таблице. Схемы питаются от источника синусоидального напряжения 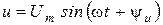 . Значения амплитуды напряжения
. Значения амплитуды напряжения 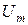 и начальной фазы
и начальной фазы 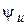 указаны в таблице, угловая частота для всех вариантов одинакова (
указаны в таблице, угловая частота для всех вариантов одинакова ( 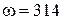 с –1), емкость, если она есть, С = 319 мкФ.
с –1), емкость, если она есть, С = 319 мкФ.
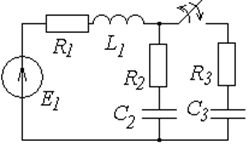
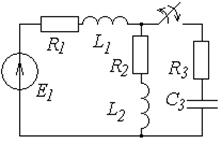
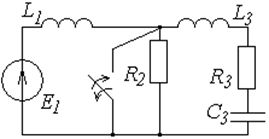
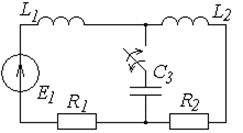
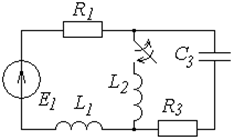
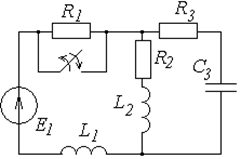
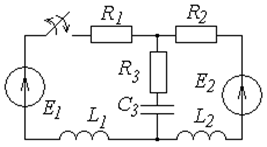
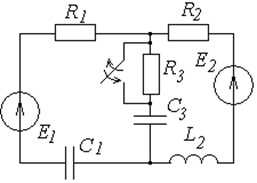
Таблица 6.1
Схемы к задаче 6.1
| № | Схема | № | Схема |
 |  | ||
 |  | ||
 |  | ||
 |  |
Окончание табл. 6.1
| № | Схема | № | Схема |
 |  | ||
 |  | ||
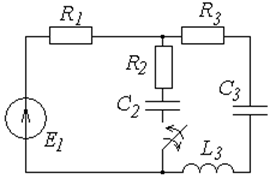 | 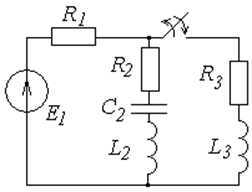 | ||
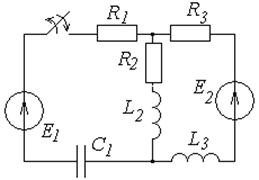 |
Таблица 6.2
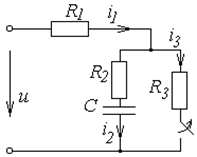
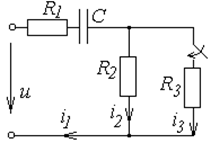
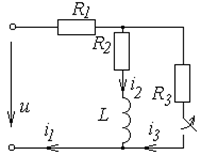
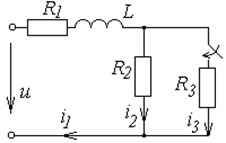
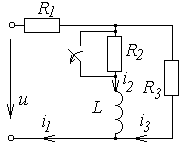
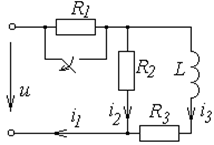
Схемы к задаче 6.2
| № | Схема | № | Схема |
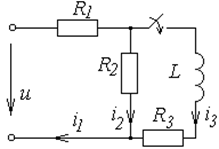 | 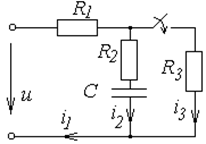 | ||
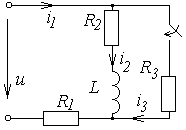 | 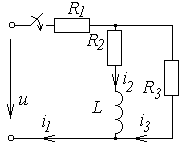 | ||
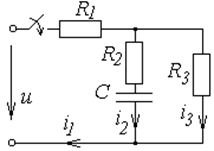 |  | ||
 |  | ||
 |  |
Окончание табл. 6.2
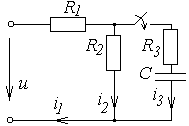 | 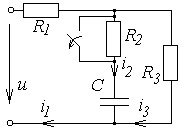 | ||
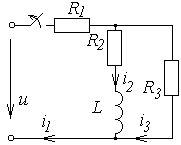 |  | ||
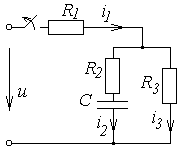 |
Таблица 6.3
Исходные данные к задаче 6.2
| Вариант | Схема из табл.6.2 | Um | yu | R1 | R2 | R3 | L | 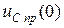 или или 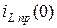 | Определить |
| В | град | Ом | Ом | Ом | мГн | ||||
| 31,8 | 0,77 A | 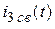 | |||||||
| 63,6 | 1,2 A | 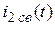 | |||||||
| – | –14 B | 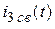 | |||||||
| 31,8 | 1,46 A | 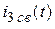 | |||||||
| – | 60 B | 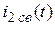 |
Продолжение табл. 6.3
| Вариант | Схема из табл.6.2 | Um | yu | R1 | R2 | R3 | L | 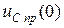 или или 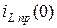 | Определить | |||
| В | град | Ом | Ом | Ом | мГн | |||||||
| – | 20 B | 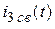 | ||||||||||
| 63,6 | –0,8 A | 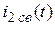 | ||||||||||
| – | –14,6 B | 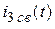 | ||||||||||
| 31,8 | 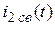 | |||||||||||
| – | 7,6 B | 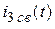 | ||||||||||
| – | –30,7 B | 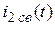 | ||||||||||
| 31,8 | –4 A | 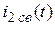 | ||||||||||
| 31,8 | 0,77 A | 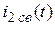 | ||||||||||
| – | 8,8 B | 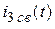 | ||||||||||
| 31,8 | –0,88 A | 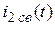 | ||||||||||
| 31,8 | –0,99 A | 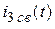 | ||||||||||
| 63,6 | –0,56 A | 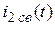 | ||||||||||
| – | –18,7 B | 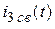 | ||||||||||
| 63,6 | –1,2 A | 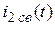 | ||||||||||
| – | 14,5 B | 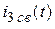 | ||||||||||
| – | –20,6 B | 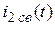 | ||||||||||
| 31,8 | –3,2 A | 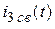 | ||||||||||
| – | –22 B | 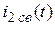 | ||||||||||
| 63,6 | 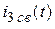 | |||||||||||
| – | 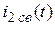 | |||||||||||
Окончание табл. 6.3
| – | –40 B | 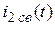 | |||||||
| 31,8 | 2 A | 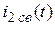 | |||||||
| 63,6 | –2,4 A | 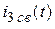 | |||||||
| – | –7,6 B | 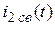 | |||||||
| 63,6 | –2,4 A | 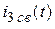 |
ЗАНЯТИЕ 7
РАСЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ С ПОМОЩЬЮ
ИНТЕГРАЛА ДЮАМЕЛЯ
Изучите теоретический материал по учебной литературе: [1, с.115–120]; [3, с.231–237] и ответьте на следующие вопросы:
1. Что такое переходная характеристика?
2. Какими должны быть независимые начальные условия при расчете переходной характеристики?
3. Как можно рассчитать переходную характеристику?
4. Какие размерности может иметь переходная характеристика?
5. В каких случаях целесообразно рассчитывать переходный процесс с помощью интеграла Дюамеля?
В качестве предварительного задания рекомендуется выполнение задачи 7.1. Для самостоятельной аудиторной работы предназначены задачи 7.2, 7.3, 7.4.
При выполнении, индивидуальных самостоятельных задач 7.1, 7.2 рекомендуется для расчета искомой функции воспользоваться классическим методом.
При решении индивидуальных аудиторных задач 7.4 необходимо обратить внимание на то, что переходная характеристика определяется как реакция на единичное ступенчатое возмущение. Такими возмущениями могут быть либо источник напряжения 1 В, либо источник тока 1 А. Независимые начальные условия (токи в индуктивных катушках и напряжения на емкостях) должны быть нулевыми.
При решении задач 7.3 и 7.5 на основе вычисленных переходных характеристик требуется рассчитать с помощью интеграла Дюамеля указанные искомые функции.
При расчетах рекомендуется использовать следующую запись интеграла Дюамеля:
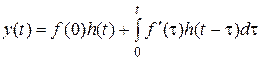 ,
,
где 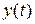 – искомая реакция;
– искомая реакция;
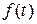 – заданное воздействие;
– заданное воздействие;
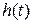 – переходная характеристика.
– переходная характеристика.
