Модуль 5. Строение атома. Атомное ядро.

Радиоактивность

Практические занятия

Примеры решения задач

Задача 1. Определить энергию, выделяемую при делении ядер урана ₉₂U²³⁵ массой m = 1кг. При делении одного ядра выделяется энергия e =200 МэВ.

Решение. При делении урана выделится энергия

Е = Ne, (1)

где N — число атомов (ядер).

Число ядер в данной массе m урана найдем из формулы:

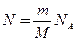, (2)

где M — молярная масса; n_a — число Авогадро.

Подставляем выражение N из (2) в формулу (1):

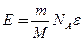. (3)

Выпишем числовые значения величин в СИ: m=1кг; M=235×10^-3 кг/моль; N_А=6,02×10²³ моль^-1; e=200 МэВ=200×1,60×10^-13 Дж=3,20×10^-11 Дж.

Проверим единицы величин правой и левой частей формулы (3):

Дж=кг/(кг×моль^-1)× моль^-1×Дж; Дж=Дж.

Вычислим

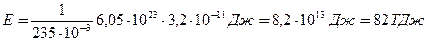
Задача 2. Определить дефект массы Dm и энергию связи DЕ ядра атома бора ₅В¹⁰.

Решение. Дефект массы ядра представляет собой разность массы нукло­нов (протонов и нейтронов), составляющих ядро, и массы ядра и определяется по формуле

Dm = Zm_p + (A— Z) т_п — т_я, (1)

где Z — зарядовое число (число протонов в ядре); т_р —масса протона; А — массовое число (общее число нуклонов в ядре); (A —Z) — число нейтронов в ядре; т_п — масса нейтрона; т_я — масса ядра.

Числа Z и А указываются при написании символа элемента: Z — слева внизу; А — справа вверху.

В данном случае для бора Z = 5, А=10.

Массу ядра найдем по формуле

т_я= т_а— Zm_e, (2)

где т_а — масса нейтрального атома; т_е — масса электрона.

Чтобы не вычислять каждый раз массу ядра, преобразуем формулу (1) с учетом (2):

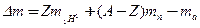, (3)

где 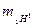— масса нейтрального атома водорода.

Из табл. 1 и 2 выпишем: 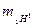=1,00783 а.е.м. *, m_n= 1,00867 а.е. м., m_a = 10,01294 а. е. м.

Подставим числовые значения в (3) и вычислим дефект массы ядра бора Dm=5×1,00783 а.е.м. + (10-5)×1,00867 а.е.м. - 10,01294 а.е.м. = 0,06956 а.е.м.

Энергия связи ядра — энергия, выделяющаяся при образовании ядра в виде электромагнитного излучения, определяется по формуле

DЕ = Dmс², (4)

где с — скорость света в вакууме.

Если энергию связи DЕ выражать в мегаэлектрон-вольтах, дефект массы ядра Dm в атомных единицах, то формула (4) принимает вид

DЕ = 931 Dm, (5)

где 931 — коэффициент, показывающий, какая энергия в мегаэлектрон-вольтах соответствует массе в 1 а. е. м.

Подставив значение в Dm (4), вычислим энергию связи: DЕ =931×0.06956 МэВ = 64,8 МэВ.

Задача 3.Вычислить энергию ядерной реакции

₈О¹⁶ + ₁Н² ® ₇N¹⁴ + ₂He⁴.

Выделяется или поглощается эта энергия?

Решение. Энергию ядерной реакции определяем по формуле

DЕ = 931Dm, (1)

где Dm — изменение массы при реакции, т.е.разность между массой частиц, вступивших в реакцию, и массой частиц, образовавшихся в результате реакции:

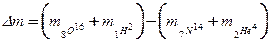(2)

Здесь 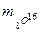— масса атома кислорода; 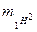— масса атома дейтерия (изотопа водорода); 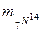— масса атома азота; 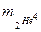— масса атома гелия. По табл. 2 находим массы атомов, подставляем в формулу (2) и вычисляем: Dm = (15,99491+2,01410)а.е.м. — (14,00307+4,00260) а.е.м. = = 0,00334 а.е.м.

Подставляем числовое значение Dm в (1) и вычисляем энергию ядерной реакции DE=931×0,0334 МэВ = 3,11 МэВ.

В результате ядерной реакции выделяется энергия, так как масса исходных ядер больше массы ядер, образовавшихся в результате реакции.

* а.е.м. — это обозначение атомной единицы массы, в которой выражаются массы молекул атомов и элементарных частиц. 1 а.е.м.= 1/12 массы атома изотопа углерода ₆С¹² (1 а. е. м.= 1,66×10^{-27 кг).}