Взаємне розміщення прямої і площини

Розглянемо деяку площину 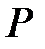і пряму 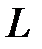, які у системі координат 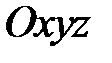задаються рівняннями

.

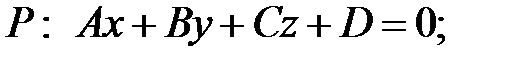
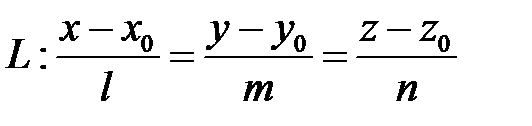Пряма може бути паралельною до площини, належати до неї або перетинати.

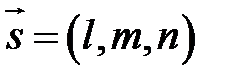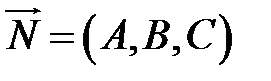Якщо пряма паралельна до площини, то вектори і перпендикулярні (Рис.34.1)

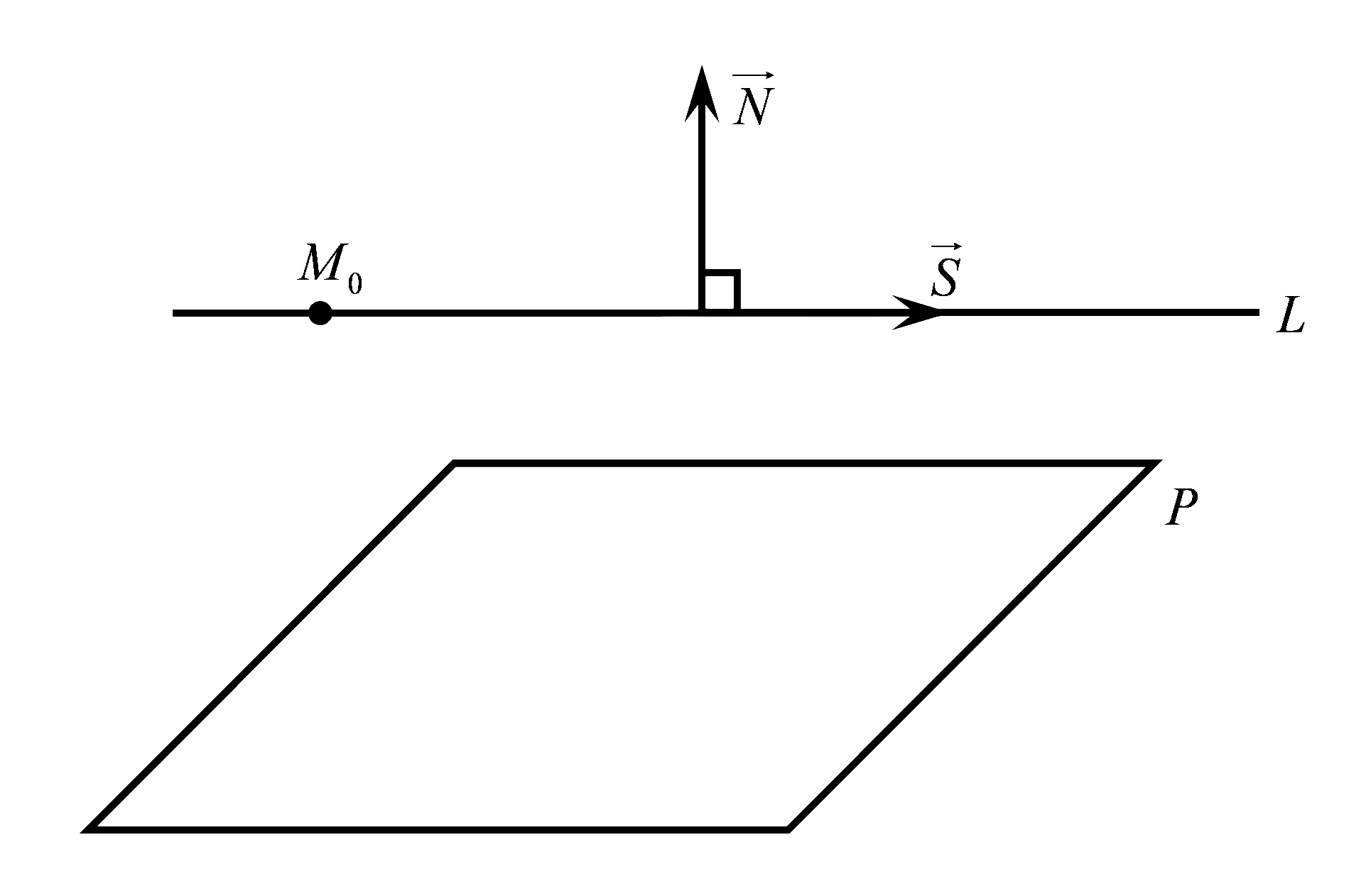
Рис.34.1

Тоді наступна умова є умовою паралельності прямої до площини

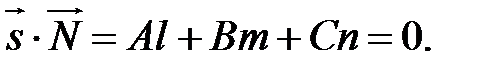
Коли пряма належить площині, то точка 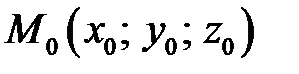є точкою площини і має задовольняти її рівняння:

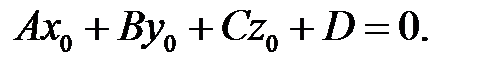
Тому умовою належності прямої до площини є одночасне виконання рівностей і .

Коли умова порушується, то пряма перетинає площину під деяким кутом. Нехай 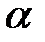- гострий кут нахилу прямої до площини (Рис.34.2)

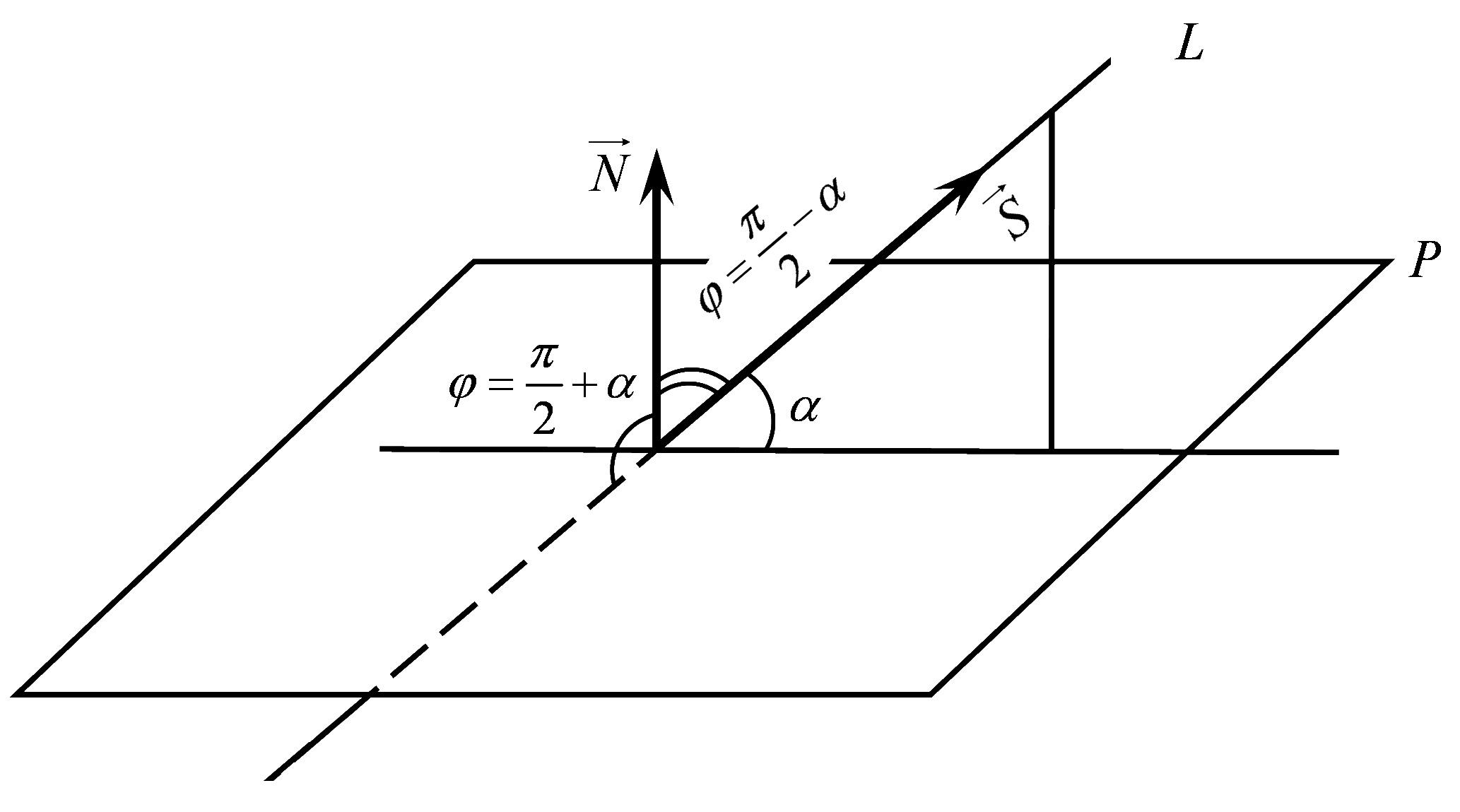
Рис.34.2

Тоді кут 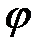між векторами 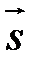і 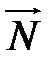дорівнює 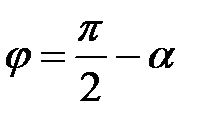або 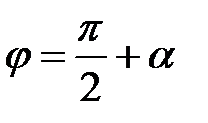. Тоді

,

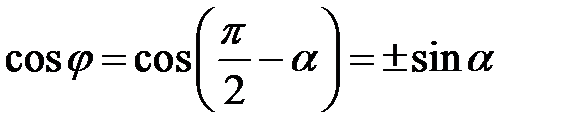або

.

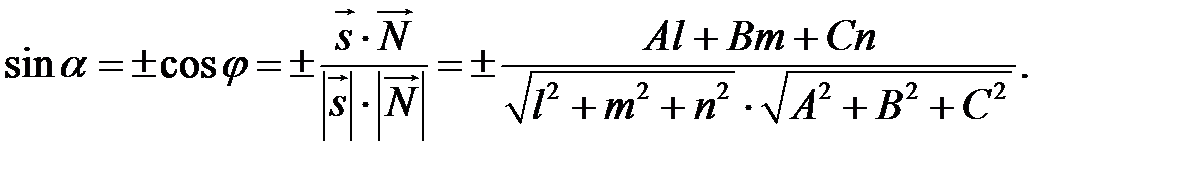
Знак у формулі обирається так, щоб отримати додатне значення 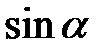.