Различные системы уравнений четырехполюсника
Изучите теоретический материал по учебной литературе: [1, с.170–172]; [2, с.257–262]; [3, с.248–255] и ответьте на следующие вопросы:
1 Что такое четырехполюсник?
2 Какие системы параметров используют для описания четырехполюсников?
3 Какие условные положительные направления токов и напряжений обычно принимаются в четырехполюсниках при различных системах параметров?
4 Какие четырехполюсники называются пассивными (обратимыми)?
5 Каким условиям удовлетворяют 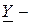 и
и 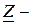 параметры пассивного четырехполюсника?
параметры пассивного четырехполюсника?
6 Какие условия накладываются на H– и G– параметры пассивного четырехполюсника?
7 Какие схемы замещения четырехполюсников применяются при расчете?
8 Какие связи существуют между параметрами четырехполюсника и параметрами схем замещения? (Показать на примере А–параметров и их связи с параметрами Т – и П – образных схем замещения).
9 Что понимают под экспериментальным определением параметров?
10 Какие четырехполюсники являются симметричными?
11 Как симметрия пассивного четырехполюсника отражается на численных значениях их параметров?
12 Сказывается ли симметрия четырехполюсников на количестве необходимых измерений для экспериментального определения параметров?
Анализ сложных электрических цепей, в том числе и электронных, можно производить используя классические универсальные методы расчета – метод контурных токов, метод узловых напряжений и т.д. В этом случае приходится решать системы уравнений, иногда довольно высоких порядков.
При изучении этого раздела теории электрических цепей следует обратить внимание на то, что можно существенно упростить задачу, если использовать представление цепи или отдельных ее частей в виде четырехполюсников. Для описания четырехполюсников можно задать различные системы параметров. Такая возможность появляется в тех случаях, когда расчетчика интересуют коэффициенты передачи тока или напряжения с входа на выход, а также входные и выходные сопротивления.
Описание объектов с помощью различных параметров, содержание этих параметров, способы их взаимной эквивалентной замены, способы экспериментального их определения и другие вопросы представляют содержание этого раздела теории электрических цепей.
В качестве предварительного задания выдается задача 9.1. Рекомендуется при ее решении воспользоваться методом контурных токов, выбрав контуры так, чтобы ток 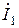 схемы (рис. 9.1) являлся контурным током первого контура, а ток
схемы (рис. 9.1) являлся контурным током первого контура, а ток 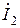 – контурным током второго контура. Затем, выполнив преобразования в системе уравнений, выделить напряжение
– контурным током второго контура. Затем, выполнив преобразования в системе уравнений, выделить напряжение 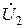 и, переместив его в правую часть системы уравнений, решить ее, установив связи между токами
и, переместив его в правую часть системы уравнений, решить ее, установив связи между токами 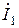 ,
, 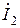 и напряжениями
и напряжениями 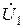 ,
, 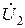 . Для решения воспользоваться правилом Крамера. После решения проанализировать содержание полученных
. Для решения воспользоваться правилом Крамера. После решения проанализировать содержание полученных 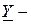 параметров.
параметров.
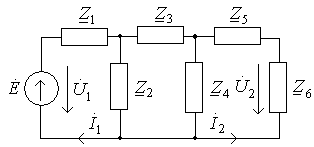
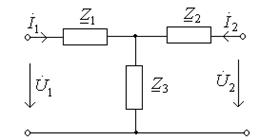
Рис. 9.1. Схема к задаче 9.1 Рис. 9.2. Схема к задаче 9.2
З а д а ч а 9. 1
Определите 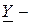 параметры четырехполюсника эквивалентной сложной цепи, представленной на рис. 9.1, установив связи между токами
параметры четырехполюсника эквивалентной сложной цепи, представленной на рис. 9.1, установив связи между токами 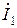 ,
, 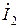 и напряжениями
и напряжениями 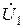 ,
, 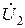 . Данные к решению задачи приведены в табл. 9.1.
. Данные к решению задачи приведены в табл. 9.1.
Таблица 9.1
Исходные данные к задаче 9.1
| Вариант | 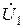 , В , В | 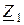 , Ом , Ом | 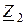 , Ом , Ом | 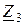 , Ом , Ом | 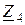 , Ом , Ом | 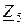 , Ом , Ом | 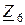 , Ом , Ом |
З а д а ч а 9. 2
Вычислите 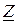 – параметры четырехполюсника, если схема его приведена на рис. 9.2, а значения сопротивлений – в табл. 9.2.
– параметры четырехполюсника, если схема его приведена на рис. 9.2, а значения сопротивлений – в табл. 9.2.
Таблица 9.2
Исходные данные к задаче 9.2
| Вариант | 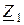 , Ом , Ом | 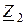 , Ом , Ом | 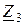 , Ом , Ом | Вариант | 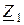 , Ом , Ом | 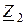 , Ом , Ом | 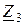 , Ом , Ом |
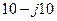 | 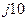 | 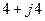 | 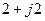 | 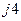 | |||
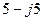 | 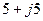 | 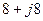 | 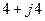 | 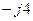 | |||
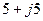 | 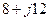 | 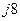 | |||||
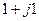 | 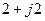 | 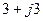 | 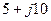 | ||||
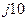 | 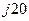 | 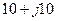 | 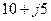 | 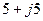 | |||
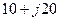 | 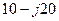 | 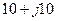 | 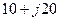 | 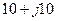 | 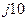 | ||
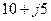 | 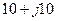 | 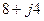 | 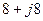 | 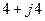 | |||
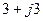 | 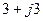 | 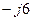 | 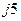 | 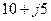 | 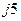 | ||
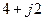 | 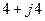 | 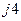 | 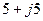 | 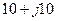 | 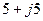 | ||
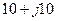 | 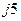 | 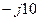 | 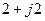 | 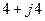 | 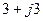 | ||
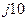 | 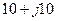 | 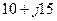 | 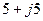 | ||||
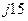 | 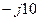 | 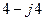 | 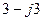 | 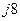 | |||
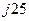 | 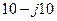 | 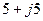 | |||||
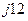 | 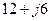 | 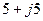 | 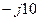 | ||||
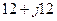 | 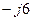 | 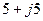 | 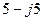 | 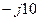 |
З а д а ч а 9. 3
Вычислите 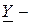 параметры четырехполюсника для схемы рис. 9.3 по данным табл. 9.3.
параметры четырехполюсника для схемы рис. 9.3 по данным табл. 9.3.
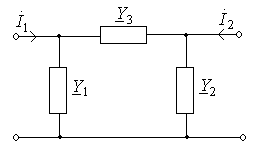
Рис. 9.3. Схема к задаче 9.3
Таблица 9.3
Исходные данные к задаче 9.3
| Вариант | 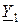 , Ом–1 , Ом–1 | 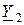 , Ом–1 , Ом–1 | 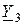 , Ом–1 , Ом–1 | Вариант | 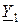 , Ом–1 , Ом–1 | 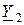 , Ом–1 , Ом–1 | 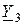 , Ом–1 , Ом–1 |
| 0,5 | 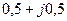 | 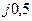 | 0,1 | 0,1 | 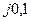 | ||
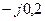 | 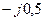 | 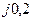 | 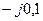 | 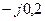 | 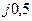 | ||
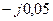 | 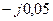 | 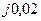 | 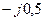 | 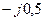 | 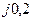 | ||
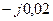 | 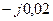 | 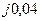 | 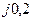 | 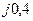 | 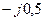 | ||
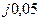 | 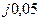 | 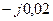 | 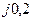 | 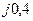 | 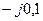 | ||
| 0,5 | 0,5 | 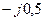 | 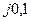 | 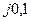 | 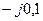 | ||
| 0,25 | 0,25 | 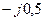 | 0,05 | 0,1 | 0,05 | ||
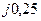 | 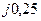 | 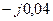 | 0,1 | 0,5 | 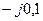 | ||
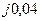 | 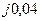 | 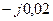 | 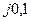 | 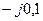 | 0,1 | ||
| 0,5 | 0,5 | 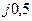 | 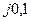 | 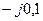 | 0,1 | ||
| 0,2 | 0,2 | 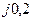 | 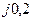 | 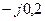 | 0,2 | ||
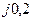 | 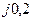 | 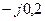 | 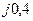 | 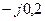 | 0,4 | ||
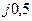 | 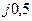 | 0,5 | 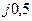 | 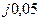 | 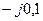 | ||
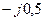 | 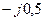 | 0,5 | 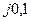 | 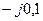 | 0,05 | ||
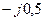 | 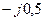 | 0,5 | 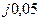 | 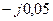 | 0,01 |
З а д а ч а 9. 4
Вычислите А–параметры четырехполюсника для схемы рис. 9.2 по данным табл. 9.2.
З а д а ч а 9. 5
Вычислите А–параметры четырехполюсника для схемы рис. 9.3 по данным табл. 9.3.
З а д а ч а 9. 6
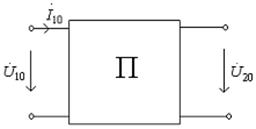
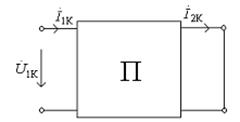
По данным измерений в режиме холостого хода и короткого замыкания рассчитаны комплексные токи и напряжения (рис. 9.4). Определите А– параметры четырехполюсника по данным табл. 9.4.
а) б)
Рис. 9.4. Четырехполюсник в режимах:
а) холостого хода; б) короткого замыкания
Таблица 9.4
Исходные данные к задаче 9.6
| Вариант | 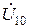 | 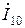 | 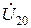 | 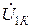 | 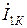 | 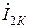 |
| В | А | В | В | А | А | |
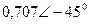 | 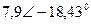 | 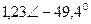 | 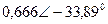 | |||
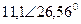 | 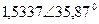 | 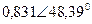 | ||||
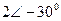 | 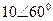 | 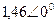 | 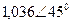 | |||
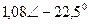 | 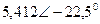 | 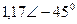 | 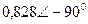 | |||
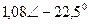 | 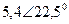 | 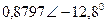 | 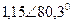 | |||
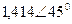 | 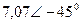 | 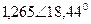 | 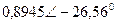 | |||
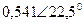 | 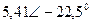 | 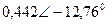 | 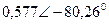 | |||
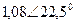 | 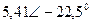 | 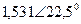 | 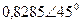 | |||
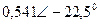 | 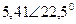 | 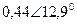 | 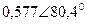 | |||
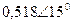 | 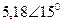 | 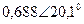 | 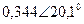 |
Окончание табл. 9.4
| Вариант | 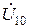 | 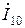 | 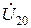 | 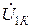 | 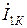 | 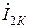 |
| В | А | В | В | А | А | |
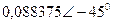 | 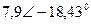 | 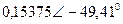 | 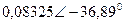 | |||
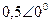 | 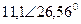 | 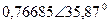 | 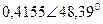 | |||
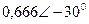 | 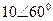 | 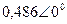 | 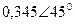 | |||
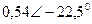 | 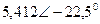 | 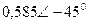 | 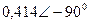 | |||
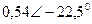 | 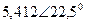 | 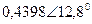 | 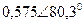 | |||
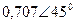 | 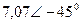 | 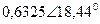 | 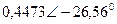 | |||
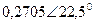 | 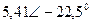 | 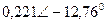 | 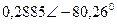 | |||
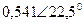 | 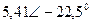 | 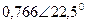 |  | |||
 |  |  | 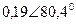 | |||
 | 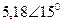 | 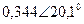 | 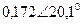 | |||
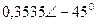 | 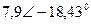 | 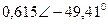 | 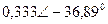 | |||
| 0,333 | 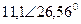 | 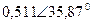 | 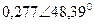 | |||
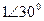 |  |  |  | |||
 | 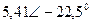 | 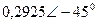 | 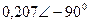 | |||
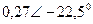 | 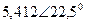 | 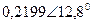 | 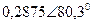 | |||
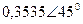 | 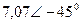 | 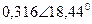 | 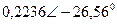 | |||
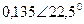 |  |  |  | |||
 | 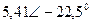 | 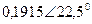 | 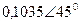 | |||
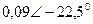 | 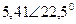 | 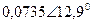 | 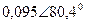 | |||
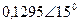 | 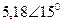 | 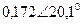 | 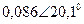 |
ЗАНЯТИЕ 10
