Отбор факторов при построении множественной регрессии
МНОЖЕСТВЕННАЯ РЕГРЕССИЯ И КОРРЕЛЯЦИЯ
СПЕЦИФИКАЦИЯ МОДЕЛИ
Парная регрессия может дать хороший результат при моделировании, если влиянием других факторов, воздействующих на объект исследования, можно пренебречь. Например, при построении модели потребления того или иного товара от дохода исследователь предполагает, что в каждой группе дохода одинаково влияние на потребление таких факторов, как цена товара, размер семьи, ее состав. Вместе с тем исследователь никогда не может быть уверен в справедливости данного предположения. Для того чтобы иметь правильное представление о влиянии дохода на потребление, необходимо изучить их корреляцию при неизменном уровне других факторов. Прямой путь решения такой задачи состоит в отборе единиц совокупности с одинаковыми значениями всех других факторов, кроме дохода. Он приводит к планированию эксперимента – методу, который используется в химических, физических, биологических исследованиях. Экономист в отличие от экспериментатора-естественника лишен возможности регулировать другие факторы. Поведение отдельных экономических переменных контролировать нельзя, т. е. не удается обеспечить равенство всех прочих условий для оценки влияния одного исследуемого фактора. В этом случае следует попытаться выявить влияние других факторов, введя их в модель, т. е. построить уравнение множественной регрессии
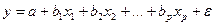 .
.
Такого рода уравнение может использоваться при изучении потребления. Тогда коэффициенты 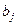 – частные производные потребления у по соответствующим факторам
– частные производные потребления у по соответствующим факторам 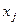 :
:
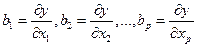
впредположении, что все остальные 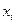 постоянны.
постоянны.
В 30-е гг. XX в. Дж.М. Кейнс сформулировал свою гипотезу потребительской функции. С того времени исследователи неоднократно обращались к проблеме ее совершенствования. Современная потребительская функция чаще всего рассматривается как модель вида
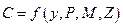 ,
,
где 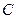 – потребление;
– потребление;
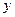 – доход;
– доход;
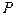 – цена, индекс стоимости жизни;
– цена, индекс стоимости жизни;
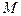 – наличные деньги;
– наличные деньги;
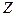 – ликвидные активы.
– ликвидные активы.
При этом 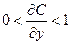 .
.
Множественная регрессия широко используется в решении проблем спроса, доходности акций, при изучении функции издержек производства, в макроэкономических расчетах и целого ряда других вопросов эконометрики. В настоящее время множественная регрессия – один из наиболее распространенных методов в эконометрике. Основная цель множественной регрессии – построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый показатель.
Построение уравнения множественной регрессии начинается с решения вопроса о спецификации модели. Спецификация включает в себя два круга вопросов: отбор факторов и выбор вида уравнения регрессии. Их решение при построении модели множественной регрессии имеет некоторую специфику, которая рассматривается ниже.
ОТБОР ФАКТОРОВ ПРИ ПОСТРОЕНИИ МНОЖЕСТВЕННОЙ РЕГРЕССИИ
Включение в уравнение множественной регрессии того или иного набора факторов связано прежде всего с представлением исследователя о природе взаимосвязи моделируемого показателя с другими экономическими явлениями. Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:
1. Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность (например, в модели урожайности качество почвы задается в виде баллов; в модели стоимости объектов недвижимости учитывается место нахождения недвижимости: районы могут быть проранжированы).
2. Факторы не должны быть интеркоррелированы и тем более находиться в точной функциональной связи.
Включение в модель факторов с высокой интеркорреляцией, когда 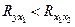 для зависимости
для зависимости 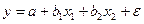 может привести к нежелательным последствиям – система нормальных уравнений может оказаться плохо обусловленной и повлечь за собой неустойчивость и ненадежность оценок коэффициентов регрессии.
может привести к нежелательным последствиям – система нормальных уравнений может оказаться плохо обусловленной и повлечь за собой неустойчивость и ненадежность оценок коэффициентов регрессии.
Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный показатель и параметры уравнения регрессии оказываются неинтерпретируемыми. Так, в уравнении 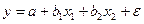 предполагается, что факторы
предполагается, что факторы 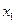 и
и 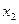 независимы друг от друга, т. е.
независимы друг от друга, т. е. 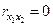 . Тогда можно говорить, что параметр
. Тогда можно говорить, что параметр 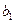 измеряет силу влияния фактора
измеряет силу влияния фактора 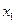 , на результат
, на результат 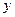 при неизменном значении фактора
при неизменном значении фактора 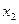 . Если же
. Если же 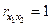 , то с изменением фактора
, то с изменением фактора 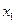 , фактор
, фактор 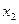 не может оставаться неизменным. Отсюда
не может оставаться неизменным. Отсюда 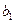 и
и 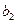 нельзя интерпретировать как показатели раздельного влияния
нельзя интерпретировать как показатели раздельного влияния 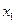 и
и 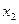 и на
и на 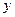 .
.
Пример. Рассмотрим регрессию себестоимости единицы продукции (руб., 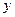 ) от заработной платы работника (руб.,
) от заработной платы работника (руб., 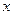 ) и производительности его труда (единиц в час,
) и производительности его труда (единиц в час, 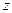 ):
):
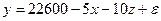 .
.
Коэффициент регрессии при переменной 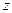 показывает, что с ростом производительности труда на 1 ед. себестоимость единицы продукции снижается в среднем на 10 руб. при постоянном уровне оплаты труда. Вместе с тем параметр при
показывает, что с ростом производительности труда на 1 ед. себестоимость единицы продукции снижается в среднем на 10 руб. при постоянном уровне оплаты труда. Вместе с тем параметр при 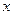 нельзя интерпретировать как снижение себестоимости единицы продукции за счет роста заработной платы. Отрицательное значение коэффициента регрессии при переменной
нельзя интерпретировать как снижение себестоимости единицы продукции за счет роста заработной платы. Отрицательное значение коэффициента регрессии при переменной 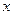 в данном случае обусловлено высокой корреляцией между
в данном случае обусловлено высокой корреляцией между 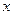 и
и 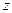 . (
. ( 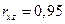 ). Поэтому роста заработной платы при неизменности производительности труда (если не брать во внимание проблемы инфляции) быть не может.
). Поэтому роста заработной платы при неизменности производительности труда (если не брать во внимание проблемы инфляции) быть не может.
Включаемые во множественную регрессию факторы должны объяснить вариацию независимой переменной. Если строится модель с набором 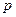 факторов, то для нее рассчитывается показатель детерминации
факторов, то для нее рассчитывается показатель детерминации 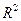 , который фиксирует долю объясненной вариации результативного признака за счет рассматриваемых в регрессии
, который фиксирует долю объясненной вариации результативного признака за счет рассматриваемых в регрессии 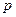 факторов. Влияние других не учтенных в модели факторов оценивается как
факторов. Влияние других не учтенных в модели факторов оценивается как 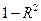 с соответствующей остаточной дисперсией
с соответствующей остаточной дисперсией 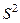 .
.
При дополнительном включении в регрессию 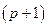 -го фактора коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться:
-го фактора коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться:
Если же этого не происходит и данные показатели практически мало отличаются друг от друга, то включаемый в анализ фактор 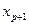 не улучшает модель и практически является лишним фактором. Так, если для регрессии, включающей пять факторов, коэффициент детерминации составил 0,857, и включение шестого фактора дало коэффициент детерминации 0,858, то вряд ли целесообразно дополнительно включать в модель этот фактор.
не улучшает модель и практически является лишним фактором. Так, если для регрессии, включающей пять факторов, коэффициент детерминации составил 0,857, и включение шестого фактора дало коэффициент детерминации 0,858, то вряд ли целесообразно дополнительно включать в модель этот фактор.
Насыщение модели лишними факторами не только не снижает величину остаточной дисперсии и не увеличивает показатель детерминации, но и приводит к статистической незначимости параметров регрессии по 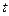 -критерию Стьюдента.
-критерию Стьюдента.
Таким образом, хотя теоретически регрессионная модель позволяет учесть любое число факторов, практически в этом нет необходимости. Отбор факторов производится на основе качественного теоретико-экономического анализа. Однако теоретический анализ часто не позволяет однозначно ответить на вопрос о количественной взаимосвязи рассматриваемых признаков и целесообразности включения фактора в модель. Поэтому отбор факторов обычно осуществляется в две стадии: на первой подбираются факторы исходя из сущности проблемы; на второй – на основе матрицы показателей корреляции определяют 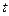 -статистики для параметров регрессии.
-статистики для параметров регрессии.
Коэффициенты интеркорреляции (т.е. корреляции между объясняющими переменными) позволяют исключать из модели дублирующие факторы. Считается, что две переменных явно коллинеарны, т. е. находятся между собой в линейной зависимости, если 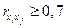 .
.
Поскольку одним из условий построения уравнения множественной регрессии является независимость действия факторов, т.е. 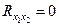 , коллинеарность факторов нарушает это условие. Если факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии. Предпочтение при этом отдается не фактору, более тесно связанному с результатом, а тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами. В этом требовании проявляется специфика множественной регрессии как метода исследования комплексного воздействия факторов в условиях их независимости друг от друга.
, коллинеарность факторов нарушает это условие. Если факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии. Предпочтение при этом отдается не фактору, более тесно связанному с результатом, а тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами. В этом требовании проявляется специфика множественной регрессии как метода исследования комплексного воздействия факторов в условиях их независимости друг от друга.
Пусть, например, при изучении зависимости 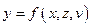 матрица парных коэффициентов корреляции оказалась следующей:
матрица парных коэффициентов корреляции оказалась следующей:
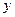 | 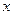 | 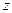 | 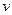 | |
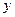 | ||||
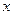 | 0,8 | |||
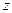 | 0,7 | 0,8 | ||
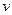 | 0,6 | 0,5 | 0,2 |
Очевидно, что факторы 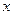 и
и 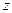 дублируют друг друга. В анализ целесообразно включить фактор
дублируют друг друга. В анализ целесообразно включить фактор 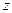 , а не
, а не 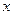 , так как корреляция
, так как корреляция 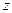 с результатом
с результатом 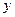 слабее, чем корреляция фактора
слабее, чем корреляция фактора 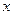 с
с 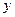 (
( 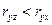 ), но зато слабее межфакторная корреляция
), но зато слабее межфакторная корреляция 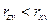 . Поэтому в данном случае в уравнение множественной регрессии включаются факторы
. Поэтому в данном случае в уравнение множественной регрессии включаются факторы 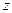 ,
, 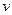 .
.
По величине парных коэффициентов корреляции обнаруживается лишь явная коллинеарность факторов. Наибольшие трудности в использовании аппарата множественной регрессии возникают при наличии мулътиколлинеарности факторов, когда более чем два фактора связаны между собой линейной зависимостью, т. е. имеет место совокупное воздействие факторов друг на друга. Наличие мультиколлинеарности факторов может означать, что некоторые факторы будут всегда действовать в унисон. В результате вариация в исходных данных перестает быть полностью независимой, и нельзя оценить воздействие каждого фактора в отдельности. Чем сильнее мультиколлинеарность факторов, тем менее надежна оценка распределения суммы объясненной вариации по отдельным факторам с помощью метода наименьших квадратов (МНК).
Если рассматривается регрессия 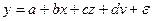 , то для расчета параметров, применяя МНК, предполагается равенство
, то для расчета параметров, применяя МНК, предполагается равенство
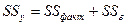
где 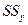 – общая сумма квадратов отклонений
– общая сумма квадратов отклонений 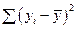 ;
;
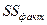 – факторная (объясненная) сумма квадратов отклонений
– факторная (объясненная) сумма квадратов отклонений 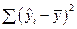
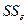 – остаточная сумма квадратов отклонений
– остаточная сумма квадратов отклонений 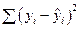
В свою очередь, при независимости факторов друг от друга выполнимо равенство
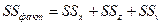 ,
,
где 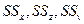 – суммы квадратов отклонений, обусловленные влиянием соответствующих факторов.
– суммы квадратов отклонений, обусловленные влиянием соответствующих факторов.
Если же факторы интеркоррелированы, то данное равенство нарушается.
Включение в модель мультиколлинеарных факторов нежелательно в силу следующих последствий:
· затрудняется интерпретация параметров множественной регрессии как характеристик действия факторов в «чистом» виде, ибо факторы коррелированы; параметры линейной регрессии теряют экономический смысл;
· оценки параметров ненадежны, обнаруживают большие стандартные ошибки и меняются с изменением объема наблюдений (не только по величине, но и по знаку), что делает модель непригодной для анализа и прогнозирования.
Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами.
Если бы факторы не коррелировали между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной матрицей, поскольку все недиагональные элементы 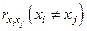 были бы равны нулю. Так, для включающего три объясняющих переменных уравнения
были бы равны нулю. Так, для включающего три объясняющих переменных уравнения
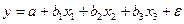
матрица коэффициентов корреляции между факторами имела бы определитель, равный единице.
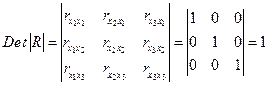 .
.
Если же, наоборот, между факторами существует полная линейная зависимость и все коэффициенты корреляции равны единице, то определитель такой матрицы равен нулю:
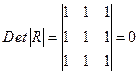 .
.
Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.
Оценка значимости мультиколлинеарности факторов может быть проведена методом испытания гипотезы о независимости переменных 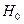 :
: 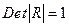 . Доказано, что величина
. Доказано, что величина 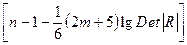 имеет приближенное распределение
имеет приближенное распределение 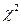 с
с 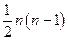 степенями свободы. Если фактическое значение
степенями свободы. Если фактическое значение 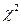 превосходит табличное (критическое)
превосходит табличное (критическое) 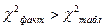 , то гипотеза
, то гипотеза 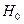 отклоняется. Это означает, что
отклоняется. Это означает, что 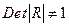 , недиагональные ненулевые коэффициенты корреляции указывают на коллинеарность факторов. Мультиколлинеарность считается доказанной.
, недиагональные ненулевые коэффициенты корреляции указывают на коллинеарность факторов. Мультиколлинеарность считается доказанной.
Через коэффициенты множественной детерминации можно найти переменные, ответственные за мультиколлинеарность факторов. Для этого в качестве зависимой переменной рассматривается каждый из факторов. Чем ближе значение коэффициента множественной детерминации к единице, тем сильнее проявляется мультиколлинеарность факторов. Сравнивая между собой коэффициенты множественной детерминации факторов, можно выделить переменные, ответственные за мультиколлинеарность, следовательно, можно решать проблему отбора факторов, оставляя в уравнении факторы с минимальной величиной коэффициента множественной детерминации.
Существует ряд подходов преодоления сильной межфакторной корреляции:
1) Самый простой путь устранения мультиколлинеарности состоит в исключении из модели одного или нескольких факторов.
2) Другой подход связан с преобразованием факторов, при котором уменьшается корреляция между ними. Например, при построении модели на основе рядов динамики переходят от первоначальных данных к первым разностям уровней 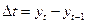 , чтобы исключить влияние тенденции, или используются такие методы, которые сводят к нулю межфакторную корреляцию, т. е. переходят от исходных переменных к их линейным комбинациям, не коррелированных друг с другом (метод главных компонент).
, чтобы исключить влияние тенденции, или используются такие методы, которые сводят к нулю межфакторную корреляцию, т. е. переходят от исходных переменных к их линейным комбинациям, не коррелированных друг с другом (метод главных компонент).
3) Одним из путей учета внутренней корреляции факторов является переход к совмещенным уравнениям регрессии, т. е. к уравнениям, которые отражают не только влияние факторов, но и их взаимодействие. Так, если 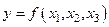 , то возможно построение следующего совмещенного уравнения:
, то возможно построение следующего совмещенного уравнения:
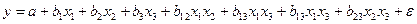 .
.
Рассматриваемое уравнение включает взаимодействие первого порядка (взаимодействие двух факторов). Возможно включение в модель и взаимодействий более высокого порядка, если будет доказана их статистическая значимость по  -критерию Фишера, например,
-критерию Фишера, например, 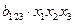 – взаимодействие второго порядка и т. д. Как правило, взаимодействия третьего и более высоких порядков оказываются статистически незначимыми, совмещенные уравнения регрессии ограничиваются взаимодействиями первого и второго порядков. Но и эти взаимодействия могут оказаться несущественными, поэтому нецелесообразно полное включение в модель взаимодействий всех факторов и всех порядков. Так, если анализ совмещенного уравнения показал значимость только взаимодействия факторов
– взаимодействие второго порядка и т. д. Как правило, взаимодействия третьего и более высоких порядков оказываются статистически незначимыми, совмещенные уравнения регрессии ограничиваются взаимодействиями первого и второго порядков. Но и эти взаимодействия могут оказаться несущественными, поэтому нецелесообразно полное включение в модель взаимодействий всех факторов и всех порядков. Так, если анализ совмещенного уравнения показал значимость только взаимодействия факторов 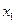 и
и 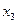 , то уравнение будет иметь вид:
, то уравнение будет иметь вид:
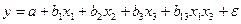 .
.
Взаимодействие факторов х, и х3 означает, что на разных уровнях фактора 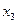 влияние фактора
влияние фактора 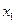 на
на 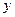 будет неодинаково, т. е. оно зависит от значений фактора
будет неодинаково, т. е. оно зависит от значений фактора 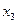 .
.
Совмещенные уравнения регрессии строятся, например, при исследовании эффекта влияния на урожайность разных видов удобрений (комбинаций азота и фосфора).
4) Решению проблемы устранения мультиколлинеарности факторов может помочь и переход к уравнениям приведенной формы. С этой целью в уравнение регрессии производится подстановка рассматриваемого фактора через выражение его из другого уравнения.
Отбор факторов, включаемых в регрессию, является одним из важнейших этапов практического использования методов регрессии. Подходы к отбору факторов на основе показателей корреляции могут быть разные. Они приводят построение уравнения множественной регрессии соответственно к разным методикам. В зависимости оттого, какая методика построения уравнения регрессии принята, меняется алгоритм ее решения на ЭВМ.
Наиболее широкое применение получили следующие методы построения уравнения множественной регрессии:
· метод исключения;
· метод включения;
· шаговый регрессионный анализ.
Каждый из этих методов по-своему решает проблему отбора факторов, давая в целом близкие результаты – отсев факторов из полного его набора (метод исключения), дополнительное введение фактора (метод включения), исключение ранее введенного фактора (шаговый регрессионный анализ).
На первый взгляд может показаться, что матрица парных коэффициентов корреляции играет главную роль в отборе факторов. Вместе с тем вследствие взаимодействия факторов парные коэффициенты корреляции не могут в полной мере решать вопрос о целесообразности включения в модель того или иного фактора. Эту роль выполняют показатели частной корреляции, оценивающие в чистом виде тесноту связи фактора с результатом. Матрица частных коэффициентов корреляции наиболее широко используется в процедуре отсева факторов. При отборе факторов рекомендуется пользоваться следующим правилом: число включаемых факторов обычно в 6–7 раз меньше объема совокупности, по которой строится регрессия. Если это соотношение нарушено, то число степеней свободы остаточной вариации очень мало. Это приводит к тому, что параметры уравнения регрессии оказываются статистически незначимыми, а F-критерий меньше табличного значения.
