Информационные характеристики непрерывных каналов связи

Модели непрерывных каналов связи. Каналы, используемые для передачи непрерывных сигналов, принято называть непрерывными. Такие каналы до сих пор находят широкое применение, например, в технике телефонной связи, радиовещании.

Реальные непрерывные каналы представляют собой сложные инерционные нелинейные объекты, характеристики которых случайным образом изменяются во времени. Для анализа таких каналов разработаны математические модели различных уровней сложности и степени адекватности реальным каналам. Модели, получившие наиболее широкое распространение, — это разновидности гауссова канала.

Под гауссовым каналом понимают математическую модель реального канала, построенную при следующих допущениях:

1) основные физические параметры канала являются известными детерминированными величинами;

2) полоса пропускания канала ограничена частотой FK герц;

3) в канале действует аддитивный гауссовый белый шум — аддитивная флуктуационная помеха ограниченной мощности с равномерным частотным спектром и нормальным распределением амплитуд.

Предполагается также, что по каналу передаются сигналы с постоянной средней мощностью, статистические связи между сигналами и шумом отсутствуют, ширина спектра сигнала и помехи ограничена полосой пропускания канала.

При рассмотрении информационных характеристик канала (скорости передачи, пропускной способности, коэффициента использования) основное внимание будет уделено гауссовому каналу.

Скорость передачи информации по непрерывному каналу. Скорость передачи информации по непрерывному каналу — это количество информации, которое передается в среднем принятыми непрерывными сигналами υ(t), относительно переданных u(t) в единицу времени.

Поскольку полоса пропускания канала всегда ограничена, непрерывные сообщения на достаточно продолжительном интервале времени Т с некоторой погрешностью могут быть представлены последовательностями отсчетов. С учетом наличия корреляционных связей между отсчетами и конечной верности воспроизведения, обусловленной воздействием помехи, для средней скорости Ĩ(VU) передачи информации дискретизованным сигналом получаем

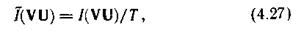
где I(VU) определяется выражением, аналогичным (4.25).

По мере увеличения длительности Т эта скорость возрастает, так как при каждом новом отсчете реализации уточняются. В пределе при Т→∞ N-мерные распределения становятся бесконечномерными и выражение (4.27) будет определять скорость передачи информации по непрерывному каналу:

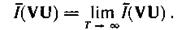
Переход к пределу при Т→∞ также означает усреднение скорости по всем возможным сигналам.

Степень вредного воздействия помехи с известными статистическими свойствами на различные ансамбли входных сигналов различна. Вследствие этого различны и значения скорости передачи информации.

Пропускная способность непрерывного канала связи. Максимально возможную скорость Сн передачи информации по непрерывному каналу с известными техническими характеристиками называют пропускной способностью непрерывного канала:

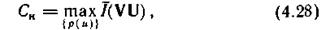
где максимум находят по всем возможным ансамблям входных сигналов.

Определим скорость передачи информации по гауссову каналу.

Пусть по гауссову каналу передается непрерывный сигнал uT(t) из ансамбля {uT(t)} со средней мощностью Рu, равной дисперсии σ . На выходе канала получим сигнал vT(t) из ансамбля {vT(t)}, искаженный гауссовой помехой ξ(t), среднюю мощность которой обозначим Ρξ(Ρξ = σ ).

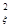Будем считать, что длительность Т сигнала uT(t) достаточно велика, чтобы с приемлемой погрешностью можно было заменить uт(t) и νт (t) последовательностями отсчетов, взятых через интервалы Δt = 1/(2Fк), где Fк — полоса пропускания канала.

В соответствии с (4.17) выражение для среднего количества информации, передаваемой сигналом vT(t), принимает вид

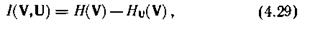
где Н(V) и HU(V) — априорная и апостериорная энтропии N-мерного случайного вектора V, составляющими которого являются случайные величины V1, V2, ...,VN.

Поскольку помеха в канале аддитивна и статистически не связана с входным сигналом, справедливо равенство

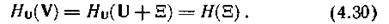
Величина Н(Ξ) в (4.30) представляет собой энтропию N-мерного случайного вектора помехи Ξ, составляющими которого являются случайные величины Ξ1, Ξ2, ..., ΕΝ.

Учитывая, что значения белого шума в моменты отсчетов будут некоррелированными, запишем

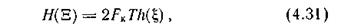
где h(ξ) — дифференциальная энтропия одного отсчетного значения помехи.

Для помехи с нормальным распределением и дисперсией σ она составит (3.49)

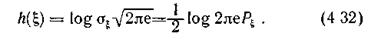
Будем считать, что отсчетные значения входных функций uT(t) независимы. При воздействии на них независимых значений помехи отсчетные значения выходных сигналов VT(t) также независимы.

Тогда H(V) можно выразить через дифференциальную энтропию h(V) одного отсчета выходного сигнала:

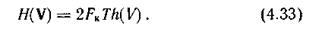
Подставив (4.32) и (4.33) в (4.29), получим

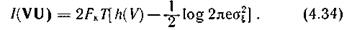
Соответственно скорость передачи информации по непрерывному каналу связи

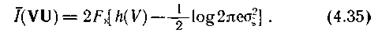
Определим теперь пропускную способность гауссова канала.

Найдем ансамбль входных сигналов, при котором обеспечивается максимальное значение h(V) в выражении (4.35).

Так как выходные сигналы образуются в результате суммирования входных сигналов и помехи, средние мощности которых ограничены, то и средняя мощность выходных сигналов ограничена. Для таких сигналов, как было установлено (см. § 3.5), наибольшее значение h(V) достигается при распределении V по нормальному закону. Известно также, что сумма двух нормально распределенных случайных величин имеет такую же функцию распределения с суммарной дисперсией. Отсюда следует, что при нормально распределенной помехе ξ выходной сигнал V будет распределен по нормальному закону лишь при нормально распределенном входном сигнале u.

Наибольшее значение энтропии h(V), а следовательно, и максимальная скорость передачи информации могут быть достигнуты при использовании нормальных центрированных случайных сигналов. Центрированность сигнала при заданной средней мощности соответствует максимальному значению дисперсии.

Они также должны иметь широкий и равномерный энергетический спектр, поскольку только в этом случае можно говорить о независимости отсчетов и использовать соотношение (2.23).

Таким образом, для более полного использования возможностей канала передаваемый сигнал должен обладать свойствами помехи, т. е. должен быть шумоподобным.

Максимальная величина дифференциальной энтропии

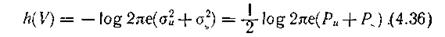
Подставляя (4.36) в (4.35), получаем выражение для пропускной способности гауссова канала:

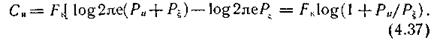
Выясним, как зависит пропускная способность гауссова канала от ширины полосы пропускания FK.

Из выражения (4.37) следует, что эта зависимость нелинейна, поскольку FK также влияет на мощность помехи. Учитывая равномерность энергетического спектра белого шума, представим его мощность Р через удельную мощность Р0 на единицу частоты.

Выражение (4.37) примет вид

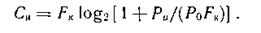
Рост пропускной способности канала при неограниченном расширении его полосы пропускания ограничен пределом СM:

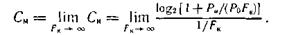
Обозначив 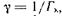по правилу Лопиталя определяем предел Сн при :

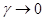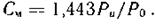
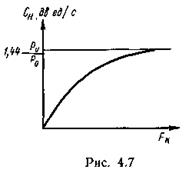
О характере зависимости 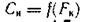можно судить по графику, представленному на рис. 4.7.

Контрольные вопросы:

1. Понятие эпсилон.
2. Каковы информационные характеристики источника непрерывных сообщений?
3. Какие бывают информационные характеристики непрерывных каналов связи?

Тема 10. Эффективное кодирование. Основная теорема Шеннона о кодировании для канала без помех

Цель лекции: Изучить эффективное кодирование

Вопросы:

1. Понятие эффективного кодирования

2. Теорема Шеннона