Теорема об обращении в ноль определителя Вронского для линейно зависимой системы функций
Определителем Вронского (вронскианом) системы n - 1 раз дифференцируемых функций y1(x), y2(x), …, yn(x) называется определитель
 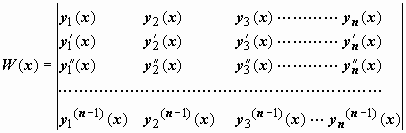 . . | (26) |
 Теорема о вронскиане линейно зависимой системы функций. Если система функций y1(x), y2(x), …, yn(x) линейно зависима на интервале (a, b), то вронскиан этой системы тождественно равен нулю на этом интервале.
Теорема о вронскиане линейно зависимой системы функций. Если система функций y1(x), y2(x), …, yn(x) линейно зависима на интервале (a, b), то вронскиан этой системы тождественно равен нулю на этом интервале.
 Док-во. Если функции y1(x), y2(x), …, yn(x) линейно зависимы на интервале (a, b), то найдутся числа
Док-во. Если функции y1(x), y2(x), …, yn(x) линейно зависимы на интервале (a, b), то найдутся числа 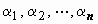 , из которых хотя бы одно отлично от нуля, такие что
, из которых хотя бы одно отлично от нуля, такие что
 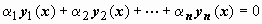 для для 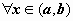 . . | (27) |
 Продифференцируем по x равенство (27) n - 1 раз и составим систему уравнений
Продифференцируем по x равенство (27) n - 1 раз и составим систему уравнений 
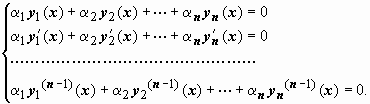
 Будем рассматривать эту систему как однородную линейную систему алгебраических уравнений относительно
Будем рассматривать эту систему как однородную линейную систему алгебраических уравнений относительно 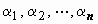 . Определитель этой системы - определитель Вронского (26). При
. Определитель этой системы - определитель Вронского (26). При 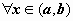 эта система имеет нетривиальное решение
эта система имеет нетривиальное решение 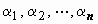 , следовательно, в каждой точке её определитель равен нулю. Итак, W(x) = 0 при
, следовательно, в каждой точке её определитель равен нулю. Итак, W(x) = 0 при 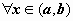 , т.е.
, т.е. 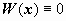 на (a, b).
на (a, b).
