Учет сил притяжения между молекулами

Учет сил притяжения между молекулами приводит к тому, что давление реального газа при равных условиях будет меньше, чем в случае идеального газа:

,

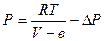отсюда

.

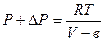Установим, от чего должно зависеть 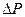. Давление, которое испытывает пристенный слой со стороны молекул газа равно силе, действующей на все молекулы на единице поверхности слоя. Очевидно, эта сила пропорциональна плотности молекул 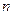. С другой стороны, число молекул в пристенном слое, испытывающих силу притяжения, также пропорционально 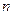. Следовательно, 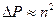. 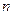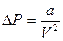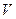Так как обратно пропорционально объему, занимаемого молем газа, то , где -молярный объем газа, 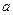-коэффициент пропорциональности, численное значение которого зависит от характера сил притяжения между молекулами.

Таким образом, давление газа с учетом сил притяжения между молекулами можно теперь написать в виде:

,

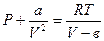отсюда

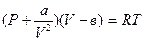. (5.5)

Это уравнение является уравнением состояния одного моля реального газа, называемым уравнением состояния реального газа. Для массы газа 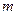уравнение Ван-дер-Ваальса имеет вид:

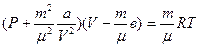. (5.6)

Здесь 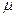-молярная масса газа. Коэффициенты 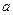и 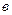в уравнении (5.6) считаются постоянными, численные значения которых для различных газов различны.

Изотермы Ван-дер-Ваальса

Уравнение Ван-дер-Ваальса (5.5) после приведения к общему знаменателю и собрания всех членов при одинаковых степенях V будет иметь вид:

.

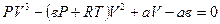Разделив на Р обе части этого равенства, получим:

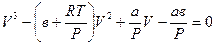. (5.7)

Это уравнение третьей степени относительно 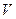и оно имеет три корня. Это значит, что при данных значениях температуры и давления возможно три значения объема. Три корня уравнения (5.7) могут быть либо все вещественными, либо два из них мнимые и одна вещественная. Возможен случай, когда все три корня уравнения (5.7) совпадают, т.е. являются точным кубом изотермы уравнения состояния. Изотерма Ван-дер-Ваальса имеет вид, показанный на рис.2. Напомним, что изотерма идеального газа имеет вид гиперболы. Как следует из рисунка кривая изотермы Ван-дер-Ваальса имеет максимум и минимум, причем данному давлению Р₁ соответствуют три значения молярного объема 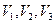. Очевидно, минимальному значению объема 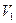соответствует жидкое состояние, максимальному объему 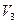- газообразное. Остается невыясненным значение объема .

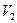Для этого рассмотрим экспериментальную изотерму реального газа, полученную путем сжатия исследуемого газа, помещенного в цилиндр с поршнем (рис.3). На этом рисунке М - манометр для измерения давления газа. Как показывает опыт, проведенный при постоянной температуре, по мере подъема поршня, давление увеличивается, причем сначала обратно пропорционально объему, а затем все медленнее. Потом давление достигает некоторой ее предельной величины и дальше уже не изменяется, несмотря на то, что подъем поршня продолжается, т.е. объем все уменьшается. Как раз в это время можно заметить появление капелек жидкости на поверхности поршня. Дальнейшее продвижение поршня вверх сопровождается увеличением количества жидкости над поршнем и соответственно уменьшением количества газа над жидкостью, но при этом манометр показывает постоянное давление. Это продолжается до тех пор, пока весь объем между поршнем и стенками сосуда не окажется заполненным жидкостью. Если продолжать и после этого поднимать поршень, т.е. сжимать уже жидкость, то теперь незначительное уменьшение объема приведет к резкому возрастанию давления. Если рассмотренный процесс изобразить графически, то он имеет вид, приведенный на рисунке 4. Между изотермой Ван-дер-Ваальса и экспериментальной изотермой имеется существенное различие, как это видно из рис.4, на котором на экспериментальную кривую пунктирами наложена изотерма Ван-дер-Ваальса. Из этого рисунка видно, что вместо прямолинейного горизонтального участка 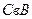изотерма Ван-дер-Ваальса в этой области имеет характерный завиток с максимумом и минимумом. Это можно объяснить, правильно анализируя изотерму. Участки ЕС и ВА изотермы Ван-дер-Ваальса совпадают, по крайней мере, качественно с соответствующими участками экспериментальной изотермы. Напомним, что участок ЕС соответствует жидкому состоянию, а ВА - газообразному. Следовательно, из уравнения Ван-дер-Ваальса следует существование двух фаз вещества. Возникает вопрос, почему не наблюдается третья фаза, изображаемая, например, точкой в на изотерме Ван-дер-Ваальса. Как видно из рисунка, состояния, отвечающие точкам на участке кривой 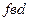, не могут существовать, так как на этом участке с возрастанием объема при постоянной температуре давление также возрастает, что является физически нереальным. Состояние системы в этой области должен быть крайне неустойчивым. Это приводит к тому, что возможные по уравнению Ван-дер-Ваальса состояния, отвечающие участку 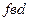, в действительности не наблюдаются. Что касается состояний, соответствующих участкам изотермы 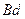и 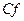, то хотя они не являются в такой степени неустойчивыми, как fвd ,но они менее устойчивы, чем состояния, отвечающие участку 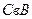. Эти состояния могут быть осуществлены, но только при соблюдении определенных условий. Вещество, состояние которого соответствует точкам участка кривой 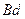, находится в газообразном состоянии, так как участок 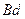является продолжением участка изотермы 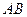. Но давление газа на этом участке выше упругости насыщенного пара при той же температуре, что противоестественно. Такой газ называют пересыщенным, или переохлажденным, поскольку его количество больше, чем необходимо для того, чтобы он был насыщенным. Состояния, изображаемые точками на участке 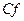также являются практически нереализуемыми из-за их малой устойчивости. Точки на этом участке отвечают жидкому состоянию, так как участок 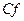является продолжением участка СЕ. Часто это состояние вещества называют перегретой жидкостью. Состояния, соответствующие участкам 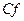, 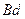в отличие от нестабильных состояний участка 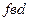, называются метастабильными.

Из уравнения состояния Ван-дер-Ваальса нельзя определить положение горизонтального участка опытной кривой относительно максимума и минимума кривой Ван-дер-Ваальса. Это значит, что нельзя определить величину равновесного давления насыщенного пара при данной температуре. Максвелл предложил провести в изотерме Ван-дер-Ваальса горизонтальный участок, соответствующий положению насыщенного пара таким образом, чтобы площади кривой изотермы выше и ниже горизонтального участка были бы равны (рис.5). Это предложение Максвелла легко обосновывается на основе термодинамического равенства Клаузиуса:

.

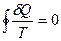Отметим, что вещество можно перевести из состояния В в состояние С двумя путями: по изотерме 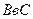двухфазного состояния вещества, и по теоретической изотерме физического однородного вещества 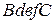, содержащий неустойчивый участок 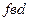. Применим равенство Клаузиуса к квазистатическому круговому процессу 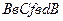Поскольку это изотермический процесс, равенство Клаузиуса примет вид: 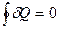. Из первого закона термодинамики 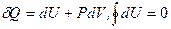, так что ,

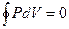или

.

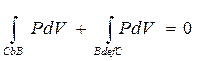Это уравнение можно переписать так:

.

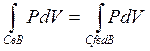Отсюда следует, что площадь прямоугольника СВМN, должна быть равна площади криволинейной фигуры 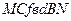. Это возможно, когда площад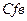и и 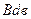равны.