Функции Minimize, Maximize

В среду MathCad версии 8 и выше введены две новые функции minimize и maximize, позволяющие решать оптимизационные задачи без вышеописанных в разделе 2.1 ухищрений. Эти функции имеют вид:

Minimize(f, var1, var2, ...);

Maximize(f, var1, var2, ...).

Функции вычисляют величины var1, var2, ..., которые удовлетворяя условиям, заданным в блоке решения делают значения функции f минимальными либо максимальными.

Аргументы:

var1, var2, ... – скалярные переменные, используемые в блоке решения. Их начальные значения должны быть заданы перед блоком решения.

f – функция, которая должна быть определена перед блоком решения.

Для нахождения минимума или максимума функции необходимо:

§ определить функцию, минимум или максимум нужно найти;

§ задать начальное приближение для всех неизвестных, которые нужно найти;

§ напечатать ключевое слово Given, начинающее блок решения;

§ ниже слова Given ввести уравнения и неравенства, определяющие область решения;

§ ввести любое выражение, которое включает функцию minimize или maximize.

Эти функции возвращают скаляр, если используется только одна переменная. Иначе результат есть вектор, первый элемент которого есть var1, второй - var2, и т. д.

Если в блоке решения нет условий, то слово Given можно не вводить.

Функции minimize и maximize нечувствительны к регистру.

Пример использования функций для нахождения экстремумов показан на рисунках 2.4 и 2.5.

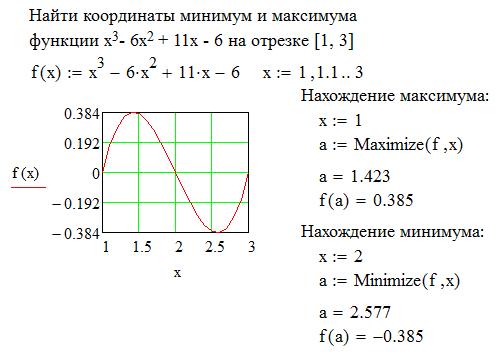Рисунок 2.4 - Пример нахождения минимума и максимума одномерной функции

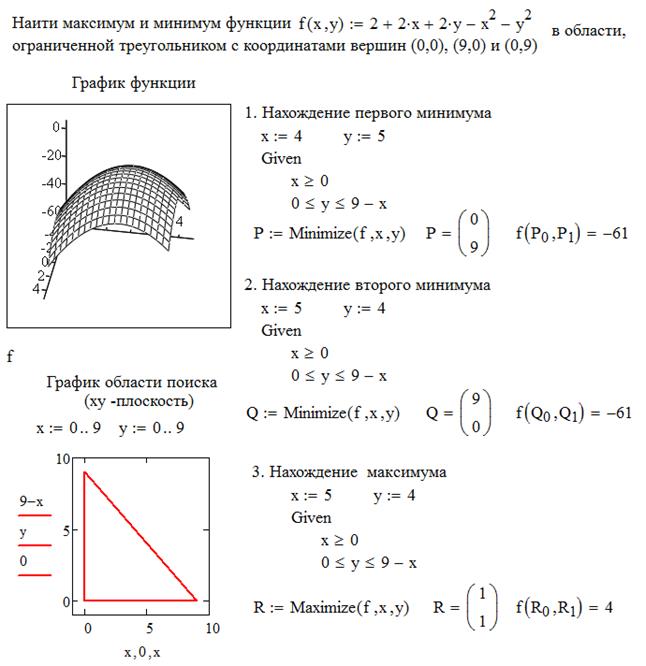Рисунок 2.5. Пример нахождения минимума и максимума двумерной функции.

ИНТЕРПОЛЯЦИЯ

Интерполяция использует значения таблично заданной функции в ряде точек (узлах интерполяции), чтобы вычислить значения этой функции в точках, лежащих между узлами. В MathCad можно соединять точки данных прямыми линиями (линейная интерполяция), фрагментами кубического полинома (кубическая сплайн-интерполяция) или полиномами. Функции интерполяции всегда определяют кривую, точно проходящую через заданные точки.

Линейная интерполяция

При линейной интерполяции MathCad соединяет существующие точки данных прямыми линиями. Это выполняется функцией

linterp ( vx, vy, x),

где: vx, vy- векторы данных, соответствующих x и y, которые должны быть одинаковой длины. Вектор vx должен содержать вещественные значения, расположенные в порядке возрастания;

x - точка, для которой нужно найти значение функции.

Эта функция соединяет точки данных отрезками прямых, создавая таким образом ломаную линию. Интерполируемое значение для заданного x есть ордината y соответствующей точки ломаной.

Для значений x, расположенных перед первой точкой в vx, MathCad продолжает ломаную прямой линией, проходящей через первые две точки данных. Для значений x, расположенных за последней точкой в vx, MathCad продолжает ломаную прямой линией, проходящей через последние две точки данных.

На рисунке 3.1 показаны некоторые примеры линейной интерполяции.

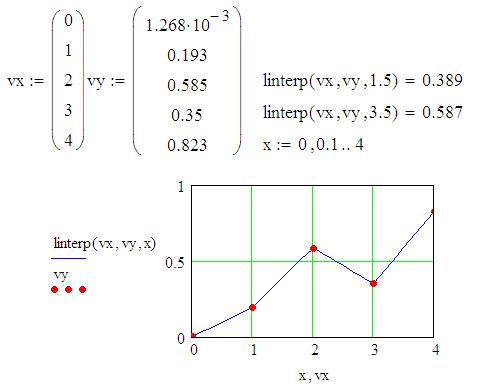Рисунок 3.1 - Примеры линейной интерполяции