Задачи для устного экзамена по геометрии на итоговой аттестации за 10 класс
Билет №1
1. Найдите диагонали равнобедренной трапеции, основания которой равны 4 см и 6 см, а боковая сторона 5 см.
2. В окружности радиуса 6 см проведена хорда АВ. Через середину М этой хорды проходит прямая, пересекающая окружность в точках С и Е. Известно, что СМ=9 см, угол АСВ=30. Найти длину СЕ.
Билет №2
- Углы АДС и АВС вписаны в окружность. Какой может быть величина угла АДС, если угол АВС=56?
- Дана прямоугольная трапеция АВСД (угол А=90). Площадь трапеции равна
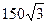 . Углы СДА и ВСА равны по 60. Найти диагональ АС.
. Углы СДА и ВСА равны по 60. Найти диагональ АС.
Билет №3
- Найдите площадь круга, если длина окружности равна
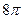 см.
см. - Площадь параллелограмма равна
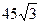 , угол А=60. АВ:АД=10:3. Биссектриса угла А пересекает сторону параллелограмма в точке М. Найдите длину отрезка АМ.
, угол А=60. АВ:АД=10:3. Биссектриса угла А пересекает сторону параллелограмма в точке М. Найдите длину отрезка АМ.
Билет №4
- Величины углов АВС и КВС относятся как 7:3, а их разность равна 72. Могут ли эти углы быть смежными?
- Найдите радиус окружности, вписанной в параллелограмм, если его диагонали равны 12 см и
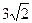 см.
см.
Билет №5
- В равностороннем треугольнике АВС проведена высота ВД. Найдите углы треугольника АВД.
- Найдите диагональ
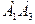 правильного восьмиугольника, если площадь треугольника
правильного восьмиугольника, если площадь треугольника 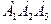 равна
равна 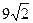 м.
м.
Билет №6
- В остроугольном равнобедренном треугольнике угол между основанием и высотой , проведённой к боковой стороне, равен 34. Найдите углы этого треугольника.
- Диагонали трапеции АВМК пересекаются в точке О. Основания трапеции ВМ и АК относятся как 2:3. Найдите площадь трапеции, если известно, что площадь треугольника АОВ равна 12.
Билет №7
- Найдите сторону и площадь ромба, если его диагонали равны 24 см и 32 см.
- Найдите площадь правильного многоугольника, если его внешний угол равен 30, а диаметр описанной около него окружности равен 8 см.
Билет №8
- Найдите катеты прямоугольного треугольника, если его гипотенуза равна
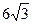 см, а один из острых углов в два раза больше другого.
см, а один из острых углов в два раза больше другого. - К окружности проведены касательные МА и МВ. Найти длину хорды АВ, если радиус окружности равен 20 см, а расстояние от точки М до хорды АВ равно 9 см.
Билет №9
- Найдите длину окружности, если площадь круга
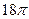 .
. - Найдите радиус окружности, вписанной в треугольник ВСД, если она касается стороны ВС в точке Р и ВД=ВС=15 см, СР=12 см.
Билет №10
- Найдите число сторон выпуклого многоугольника, сумма внутренних углов которого 4320.
- В остроугольном треугольнике АВС угол А равен 60, ВС=10 см, отрезки ВМ и СК – высоты. Найдите длину отрезка КМ.
Билет №11
- Найдите медиану прямоугольного треугольника, проведённую к гипотенузе, если его катеты 6 м и 8 см.
- Периметр описанной равнобокой трапеции равен 4а. Острый угол трапеции 60. Найдите диагональ трапеции.
Билет №12
- В прямоугольный треугольник вписана окружность радиуса 4 см. Найдите периметр этого треугольника, если его гипотенуза 26 см.
- Две стороны параллелограмма равны 13 и 14 см, а одна из диагоналей равна 15 см. Найдите площадь треугольника, отсекаемого от параллелограмма биссектрисой его угла.
Билет №13
- Найдите угол между векторами, заданными своими координатами
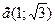 и
и 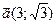
- Основание остроугольного равнобедренного треугольника равно 48 см. Найдите радиус вписанной в него окружности, если радиус описанной около него окружности равен 25 см.
Билет №14
- Найдите стороны треугольника, периметр которого равен 5,5 см, если стороны подобного ему треугольника равны 0,4 см, 0,8 см, 1 см.
- Найдите площадь параллелограмма АВСД, если его большая сторона равна
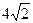 см, диагональ ВД=5 см, а угол ВАД равен 45.
см, диагональ ВД=5 см, а угол ВАД равен 45.
Билет №15
- В равностороннем треугольнике проведены две медианы. Найдите величину острого угла, образовавшегося при их пересечении.
- Равнобокая трапеция с площадью
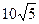 и боковым ребром 5см такова, что в неё можно вписать окружность. Найдите радиус описанной окружности.
и боковым ребром 5см такова, что в неё можно вписать окружность. Найдите радиус описанной окружности.
Билет №16
- Стороны прямоугольника равны 72 см и 8 см. Найти сторону равновеликого ему квадрата.
- На стороне ВС треугольника АВС отмечена точка К. Известно, что сумма углов В и С равна углу АКВ, АК=5 см, ВК=16 см, КС=2 см. Найдите сторону АВ.
Билет №17
- Средняя линия трапеции равна 8 см и делится диагональю на два отрезка, разность между которыми 2 см. Найдите основания трапеции.
- В треугольнике АВС проведена медиана АМ. Найдите площадь треугольника АВС, если АС=3
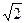 м, ВС=10м, угол МАС равен 45.
м, ВС=10м, угол МАС равен 45.
Билет №18
- Найдите углы ромба , если его периметр 8 см, а высота ромба 1см.
- В равнобедренную трапецию с боковой стороной 10м, вписана окружность радиуса 3м. Найдите площадь трапеции.
Билет №19
- Найдите периметр ромба, если один из его углов 60, а меньшая диагональ 5см.
- Площадь равнобедренного треугольника АВС с основанием ВС равна 160 квадратных метров. Боковая сторона 20м. Высоты ВК и АН пересекаются в точке О. Найдите площадь треугольника АВО.
Билет №20
- В окружность вписан прямоугольник, стороны которого 6м и 8м. Найдите длину этой окружности.
- Найдите площадь параллелограмма ОМРК, если КР=10см, МР=6см и составляет с диагональю МК угол 45.
Билет №21
- Найдите площадь круга, описанного около квадрата со стороной 6см.
- В остроугольном треугольнике АВС на стороне АС отмечена точка М, такая, что угол С равен углу АВМ. Найдите АВ, если АС=9м и отрезок АМ=4м.
Билет №22
- Найдите высоту равнобедренной трапеции. Если её основания равны 10см и 24см, а боковая сторона 25см.
- В треугольнике СЕН угол С равен 45, точка Т делит сторону СЕ на отрезки СТ=2м и ЕТ=14м. Угол СНТ равен углу СЕН. Найдите площадь треугольника СНТ.
- КА – перпендикуляр к плоскости треугольника АВС. М – середина ВС. Известно, что КМ перпендикулярна ВС.Докажите, что треугольник АВС равнобедренный. Докажите перпендикулярность плоскостей КВС и КАМ. Найдите площадь треугольника АВС, если угол ВКС=60, ВС=6, КА=
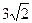 .
. - Точка S равноудалена от вершин правильного треугольника АВС на
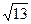 см. Найдите двугранный угол SАВС, если АВ=6.
см. Найдите двугранный угол SАВС, если АВ=6. - Точка О лежит на биссектрисе угла АВС, равного 60, DO – перпендикуляр к плоскости АВС. Докажите, что точка D равноудалена от сторон угла АВС. Докажите перпендикулярность плоскостей DAC и DOB, если DA и DC расстояния от точки D до сторон угла. Найдите DB, если АС=6, DO=4.
- Равнобедренные треугольники АВС и ADC имеют общее основание, а двугранный угол BACD – прямой. Найдите углы, образуемые прямой BD с плоскостями треугольников, если угол АВС=60, а угол ADC=90.
- В кубе
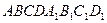 постройте и найдите угол между плоскостями
постройте и найдите угол между плоскостями 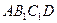 и
и 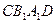 .
. - Основание пирамиды прямоугольный треугольник с катетом
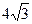 см и противолежащим углом 60. Все боковые рёбра пирамиды наклонены к плоскости основания под углом 45. Обоснуйте положение высоты пирамиды. Найдите боковые рёбра.
см и противолежащим углом 60. Все боковые рёбра пирамиды наклонены к плоскости основания под углом 45. Обоснуйте положение высоты пирамиды. Найдите боковые рёбра. - Основание пирамиды ромб с острым углом
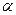 . Высота пирамиды h., а все двугранные углы при основании
. Высота пирамиды h., а все двугранные углы при основании 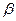 . Обоснуйте положение высоты пирамиды. Найдите площадь полной поверхности.
. Обоснуйте положение высоты пирамиды. Найдите площадь полной поверхности. - Основание пирамиды треугольник с углами
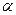 и
и 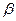 . Все боковые рёбра образуют с высотой пирамиды углы, равные
. Все боковые рёбра образуют с высотой пирамиды углы, равные 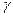 . Высота пирамиды h. Обоснуйте положение высоты. Найдите площадь основания.
. Высота пирамиды h. Обоснуйте положение высоты. Найдите площадь основания. - Основание пирамиды равнобокая трапеция с основаниями 4 и 16 см. Все боковые грани пирамиды образуют с её высотой углы в 30. Обоснуйте положение высоты пирамиды. Найдите площадь полной поверхности.
- Основание пирамиды прямоугольный треугольник с катетами 15 и 20см. Боковые грани пирамиды, содержащие катеты, перпендикулярны плоскости основания, а третья боковая грань наклонена к ней под углом 60. Обоснуйте положение высоты пирамиды. Найдите площадь полной поверхности.
- Основание пирамиды равнобедренный прямоугольный треугольник. Боковая грань, содержащая гипотенузу, перпендикулярна плоскости основания, а две другие наклонены к ней под углом
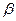 . Высота пирамиды h. Найдите площадь боковой поверхности.
. Высота пирамиды h. Найдите площадь боковой поверхности. - Найдите площадь боковой поверхности правильной треугольной усечённой пирамиды, в которой высоты оснований 6 и 9см, а двугранный угол при основании 60.
- Сечение правильного тетраэдра, проходящего через середины четырёх рёбер, имеет площадь 9 кв см. Найдите площадь полной поверхности тетраэдра.
- Основание прямой призмы равнобедренный треугольник с боковой стороной 6 см и углом при вершине 120. Диагональ наибольшей боковой грани образует с основанием призмы угол 60. Найдите площадь боковой и полной поверхности призмы.
- Боковая поверхность правильной четырёхугольной призмы имеет площадь 16. диагональ основания равна
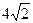 см. Найдите площадь сечения призмы, проходящего через диагонали двух смежных боковых граней, имеющие общую вершину.
см. Найдите площадь сечения призмы, проходящего через диагонали двух смежных боковых граней, имеющие общую вершину. - В наклонном параллелепипеде основание и одна из боковых граней – квадраты, плоскости которых образуют угол 30, а площадь каждого из них 36. Найдите площадь полной поверхности.
- Основание наклонной призмы – равнобедренный прямоугольный треугольник с гипотенузой 6 см. Боковое ребро, исходящее из вершины прямого угла, равно 8 см и образует с катетами треугольника равные углы 60. Найдите площадь полной поверхности призмы.
