Линейный коэффициент детерминации. 5 страница
! Если расчетное значение критерия Фишера меньше табличного значения, то гипотеза о статистической незначимости уравнения …
- отвергается;
- незначима;
+- принимается;
- несущественна.
!Если факторы входят в модель как произведение, то модель называется:
- суммарной;
- производной;
- аддитивной;
+- мультипликативной.
! Уравнение регрессии, которое связывает результирующий признак с одним из факторов при зафиксированных на среднем уровне значении других переменных, называется:
- множественным;
- существенным;
+- частным;
- несущественным.
!Относительно количества факторов, включенных в уравнение регрессии, различают …
- линейную и нелинейную регрессии;
- непосредственную и косвенную регрессии;
+- простую и множественную регрессию;
- множественную и многофакторную регрессию.
Требованием к уравнениям регрессии, параметры которых можно найти при помощи МНК является:
- равенство нулю значений факторного признака4
-нелинейность параметров;
- равенство нулю средних значений результативной переменной;
- линейность параметров.
Метод наименьших квадратов не применим для …
- линейных уравнений парной регрессии;
- полиномиальных уравнений множественной регрессии;
+- уравнений, нелинейных по оцениваемым параметрам;
- линейных уравнений множественной регрессии.
!При включении фиктивных переменных в модель им присваиваются …
- нулевые значения;
+- числовые метки;
- одинаковые значения;
- качественные метки.
!Если между экономическими показателями существует нелинейная связь, то …
- нецелесообразно использовать спецификацию нелинейного уравнения регрессии;
- целесообразно использовать спецификацию нелинейного уравнения регрессии;
- целесообразно использовать спецификацию линейного уравнение парной регрессии;
+- необходимо включить в модель другие факторы и использовать линейное уравнение множественной регрессии.
! Результатом линеаризации полиномиальных уравнений является …
- нелинейные уравнения парной регрессии;
- линейные уравнения парной регрессии;
- нелинейные уравнения множественной регрессии;
+- линейные уравнения множественной регрессии.
! В стандартизованном уравнении множественной регрессии 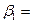 0,3;
0,3; 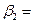 -2,1. Определите, какой из факторов
-2,1. Определите, какой из факторов 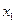 или
или 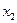 оказывает более сильное влияние на
оказывает более сильное влияние на 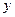 :
:
+- 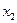 , так как 2,1>0,3;
, так как 2,1>0,3;
- по этому уравнению нельзя ответить на поставленный вопрос, так как неизвестны значения «чистых» коэффициентов регрессии;
- 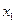 , так как 0,3>-2,1;
, так как 0,3>-2,1;
- по этому уравнению нельзя ответить на поставленный вопрос, так как стандартизированные коэффициенты несравнимы между собой.
!Факторные переменные уравнения множественной регрессии, преобразованные из качественных в количественные называются …
- аномальными;
- множественными;
- парными;
+- фиктивными.
!Оценки параметров линейного уравнения множественной регрессии можно найти при помощи метода:
- средних квадратов;
- наибольших квадратов;
- нормальных квадратов;
+- наименьших квадратов.
!Основным требованием к факторам, включаемым в модель множественной регрессии, является:
- отсутствие взаимосвязи между результатом и фактором;
- отсутствие взаимосвязи между факторами;
+- отсутствие линейной взаимосвязи между факторами;
- наличие тесной взаимосвязи между факторами.
!Фиктивные переменные включаются в уравнение множественной регрессии для учета действия на результат признаков …
+- качественного характера;
- количественного характера;
- несущественного характера;
- случайного характера.
!Из пары коллинеарных факторов в эконометрическую модель включается тот фактор,
- который при достаточно тесной связи с результатом имеет наибольшую связь с другими факторами;
- который при отсутствии связи с результатом имеет максимальную связь с другими факторами;
- который при отсутствии связи с результатом имеет наименьшую связь с другими факторами;
+- который при достаточно тесной связи с результатом имеет меньшую связь с другими факторами.
!Гетероскедастичность подразумевает …
- постоянство дисперсии остатков независимо от значения фактора;
- зависимость математического ожидания остатков от значения фактора;
+- зависимость дисперсии остатков от значения фактора;
- независимость математического ожидания остатков от значения фактора.
!Величина остаточной дисперсии при включении существенного фактора в модель:
- не изменится;
- будет увеличиваться;
- будет равно нулю;
-+ будет уменьшаться.
!Если спецификация модели отображает нелинейную форму зависимости между экономическими показателями, то нелинейно уравнение …
+- регрессии;
- детерминации;
- корреляции;
- аппроксимации.
!Исследуется зависимость, которая характеризуется линейным уравнением множественной регрессии. Для уравнения рассчитано значение тесноты связи результативной переменной с набором факторов. В качестве этого показателя был использован множественный коэффициент …
- корреляции;
- эластичности;
- регрессии;
+- детерминации.
!Строится модель зависимости спроса от ряда факторов. Фиктивной переменной в данном уравнении множественной регрессии не является _________потребителя.
+- доход;
- семейное положение;
- уровень образования;
- пол.
Для существенного параметра расчетное значение критерия Стьюдента …
+- больше табличного значения критерия;
- равно нулю;
- не больше табличного значения критерия Стьюдента;
- меньше табличного значения критерия.
!Систему МНК, построенную для оценки параметров линейного уравнения множественной регрессии можно решить …
- методом скользящего среднего;
+- методом определителей;
- методом первых разностей;
- симплекс-методом.
!Показатель, характеризующий на сколько сигм изменится в среднем результат при изменении соответствующего фактора на одну сигму, при неизменном уровне других факторов, называется ____________коэффициентом регрессии
+- стандартизованным;
- нормализованным;
- выровненным;
- центрированным.
!Мультиколлинеарность факторов эконометрической модели подразумевает …
- наличие нелинейной зависимости между двумя факторами;
-++ наличие линейной зависимости между более чем двумя факторами;
- отсутствие зависимости между факторами;
+- наличие линейной зависимости между двумя факторами.
!Обобщенный метод наименьших квадратов не используется для моделей с _______ остатками.
- автокоррелированными и гетероскедастичными;
+- гомоскедастичными;
- гетероскедастичными;
- автокоррелированными.
!Методом присвоения числовых значений фиктивным переменным не является:
- ранжирование;
- присвоение цифровых меток;
- нахождения среднего значения;
+- присвоение количественных значений.
!Обобщенный метод наименьших квадратов рекомендуется применять в случае …
- нормально распределенных остатков;
- гомоскедастичных остатков;
+- автокорреляции остатков;
- автокорреляции результативного признака.
!Отбор факторов в модель множественной регрессии при помощи метода включения основан на сравнении значений …
- общей дисперсии до и после включения фактора в модель;
- остаточной дисперсии до и после включения случайных факторов в модель;
- дисперсии до и после включения результата в модель;
+- остаточной дисперсии до и после включения фактора модель.
!Обобщенный метод наименьших квадратов используется для корректировки …
- параметров нелинейного уравнения регрессии;
- точности определения коэффициента множественной корреляции;
- автокорреляции между независимыми переменными;
+- гетероскедастичности остатков в уравнении регрессии.
!После применения обобщенного метода наименьших квадратов удается избежать_________ остатков
+- гетероскедастичности;
- нормального распределения;
- равенства нулю суммы;
- случайного характера.
!Фиктивные переменные включаются в уравнения ____________регрессии
- случайной;
- парной;
- косвенной;
+- множественной.
!Взаимодействие факторов эконометрической модели означает, что …
- влияние факторов на результирующий признак зависит от значений другого неколлинеарного им фактора;
- влияние факторов на результирующий признак усиливается, начиная с определенного уровня значений факторов;
- факторы дублируют влияние друг друга на результат;
+- влияние одного из факторов на результирующий признак не зависит от значений другого фактора.
Тема Множественная регрессия (Задачи)
Уравнение регрессии, построенное по 15 наблюдениям, имеет вид:
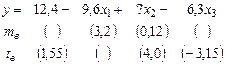
Пропущенные значения, а также доверительный интервал для
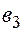 с вероятностью 0,99 равны:
с вероятностью 0,99 равны:
+— 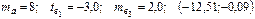
— 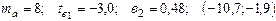
— 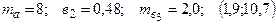
— 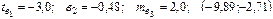
Уравнение регрессии, построенное по 20 наблюдениям, имеет вид:
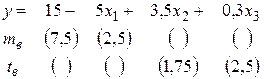
Пропущенные значения, а также доверительный интервал для 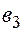 с вероятностью 0,9 равны:
с вероятностью 0,9 равны:
+— 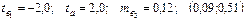
— 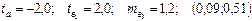
— 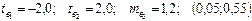
— 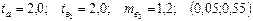
Уравнение регрессии, построенное по 16 наблюдениям, имеет вид:
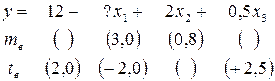
Пропущенные значения, а также доверительный интервал для 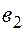 с вероятностью 0,99 равны:
с вероятностью 0,99 равны:
+— 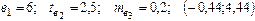
— 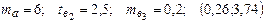
— 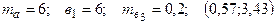
— 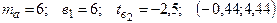
Уравнение регрессии в стандартизированном виде имеет вид:
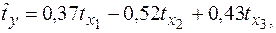
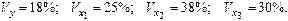
Частные коэффициенты эластичности равны:
|
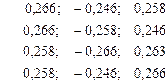
Уравнение регрессии в стандартизированном виде имеет вид:
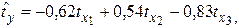
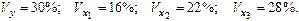
|
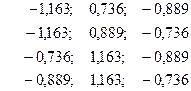
Стандартизованное уравнение регрессии имеет вид:
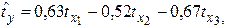
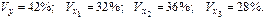
Частные коэффициенты эластичности равны:
|
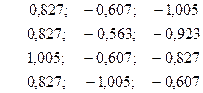
Стандартизованное уравнение регрессии имеет вид:
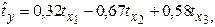
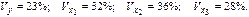
|
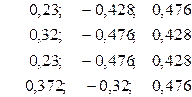
Стандартизованное уравнение регрессии имеет вид:
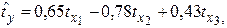
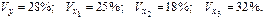
|
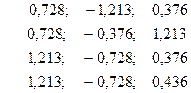
Стандартизованное уравнение регрессии имеет вид:
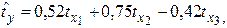
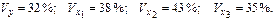
|
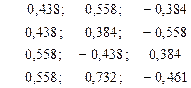
Стандартизованное уравнение регрессии имеет вид:
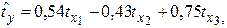
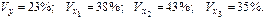
Частные коэффициенты эластичности равны:
|
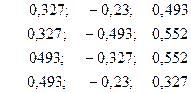
По 18 наблюдениям получены следующие данные:
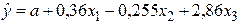
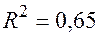 ;
; 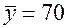 ;
; 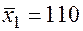 ;
; 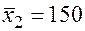 ;
; 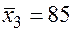
Значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра 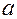 равны:
равны:
+— 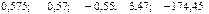
— 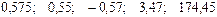
— 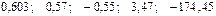
— 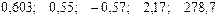
По 17 наблюдениям получены следующие данные:
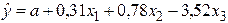
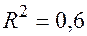 ;
; 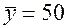 ;
; 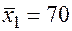 ;
; 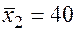 ;
; 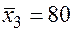
Значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра 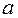 равны:
равны:
+— 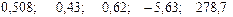
— 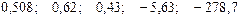
— 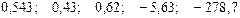
— 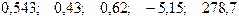
По 22 наблюдениям получены следующие данные:
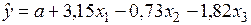
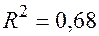 ;
; 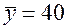 ;
; 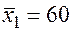 ;
; 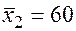 ;
; 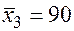
Значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра 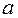 равны:
равны:
+— 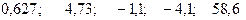
— 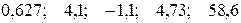
— 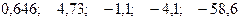
— 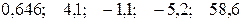
По 25 наблюдениям получены следующие данные:
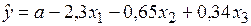
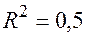 ;
; 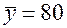 ;
; 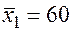 ;
; 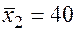 ;
; 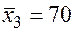
Значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра 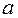 равны:
равны:
+— 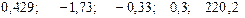
— 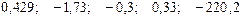
— 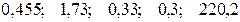
— 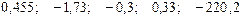
По 24 наблюдениям получены следующие данные:
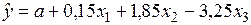
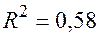 ;
; 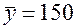 ;
; 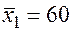 ;
; 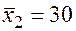 ;
; 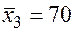
Значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра 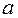 равны:
равны:
+— 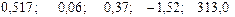
— 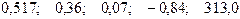
— 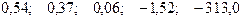
— 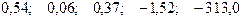
По 28 наблюдениям получены следующие данные:
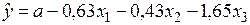
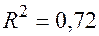 ;
; 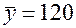 ;
; 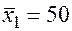 ;
; 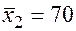 ;
; 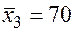
Значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра 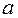 равны:
равны:
+— 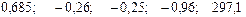
— 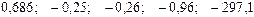
— 
— 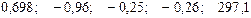
По 26 наблюдениям получены следующие данные:
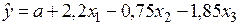
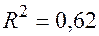 ;
; 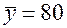 ;
; 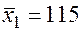 ;
; 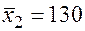 ;
; 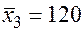
Значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра 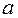 равны:
равны:
+— 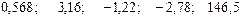
— 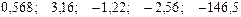
— 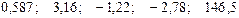
— 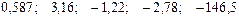
В уравнении регрессии: 
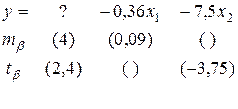
Восстановить пропущенные характеристики; построить доверительный интервал для 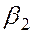 с вероятностью 0,95, если n=12
с вероятностью 0,95, если n=12
+— 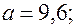
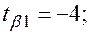
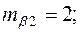 (-12,02;-2,98)
(-12,02;-2,98)
— 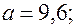
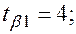
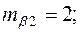 (-12,02;-2,98)
(-12,02;-2,98)
— 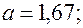
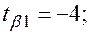
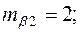 (-11,12;-3,88)
(-11,12;-3,88)
— 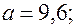
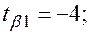
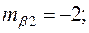 (-11,12;-3,88)
(-11,12;-3,88)
Уравнение регрессии в стандартизованном виде имеет вид:
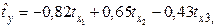
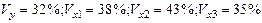
Как влияют факторы на результат и каковы значения частных коэффициентов эластичности?
+—Наибольшее влияние на результат оказывает фактор 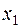 , наименьшее
, наименьшее 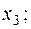
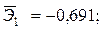
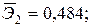
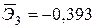
—Наибольшее влияние на результат оказывает фактор  наименьшее -
наименьшее -  ;
; 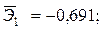
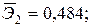
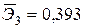
—Наибольшее влияние на результат оказывает фактор 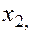 наименьшее -
наименьшее - 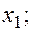
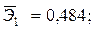
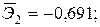
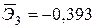
—Наибольшее влияние на результат оказывает фактор 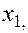 наименьшее -
наименьшее - 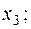
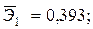
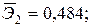
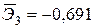
Уравнение регрессии в стандартизованном виде имеет вид:
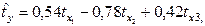
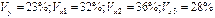
Как влияют факторы на результат и каковы значения частных коэффициентов эластичности?
+—Наибольшее влияние на результат оказывает фактор  , наименьшее
, наименьшее 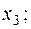
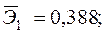
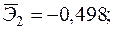
—Наибольшее влияние на результат оказывает фактор  наименьшее -
наименьшее -  ;
;