Правило лопіталя. похідні вищих порядків
Кажуть, що відношення двох функцій 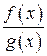 при
при 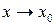 є невизначеністю виду
є невизначеністю виду 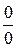 або
або 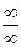 , якщо
, якщо 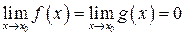 або
або 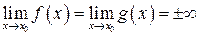 відповідно.
відповідно.
Розкрити ці невизначеності, тобто обчислити 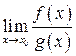 , надає можливість правило Лопіталя: якщо існує границя відношення похідних
, надає можливість правило Лопіталя: якщо існує границя відношення похідних 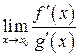 (скінченна або нескінченна), тоді існує і границя
(скінченна або нескінченна), тоді існує і границя 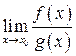 , причому справедлива формула:
, причому справедлива формула:
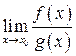 =
= 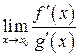 . (16)
. (16)
Зауваження 1. Якщо похідні функцій 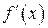 і
і 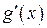 задовольняють тим самим вимогам, що і самі функції
задовольняють тим самим вимогам, що і самі функції 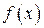 і
і 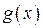 при
при 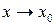 , тоді правило Лопіталя можна застосувати повторно.
, тоді правило Лопіталя можна застосувати повторно.
Приклад 1. Обчислити 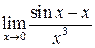 .
.
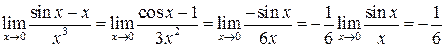 .
.
Приклад 2. Обчислити 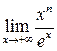 .
.
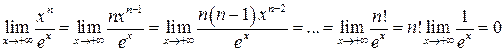 .
.
Зауваження 2.Невизначеності виду 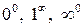 для функції
для функції 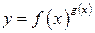 за допомогою тотожного перетворення
за допомогою тотожного перетворення 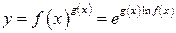 можна привести до невизначеності
можна привести до невизначеності 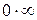 . Остання невизначеність легко зводиться до невизначеності
. Остання невизначеність легко зводиться до невизначеності 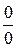 .
.
Приклад 3. Знайти 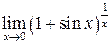 .
.
Маємо невизначеність 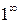 .
.
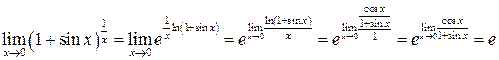 .
.
Приклад 4. Знайти 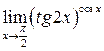 .
.
Маємо невизначеність 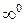 .
.
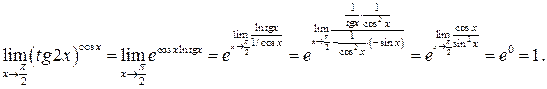
Функція 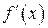 називається похідною першого порядку функції
називається похідною першого порядку функції 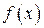 . Похідна від похідної функції
. Похідна від похідної функції 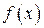 називається похідною другого порядку цієї функції:
називається похідною другого порядку цієї функції: 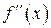 . Похідні, починаючи з другої, називаються похідними вищих порядків:
. Похідні, починаючи з другої, називаються похідними вищих порядків: 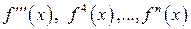 . Отже, похідна п-го порядку
. Отже, похідна п-го порядку 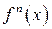 є похідна від похідної (п - 1)-го порядку.
є похідна від похідної (п - 1)-го порядку.
У механіці похідна другого порядку від функції 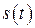 , яка описує траєкторію руху матеріальної точки, має фізичний зміст, а саме визначає прискорення точки в момент часу
, яка описує траєкторію руху матеріальної точки, має фізичний зміст, а саме визначає прискорення точки в момент часу 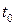 :
: 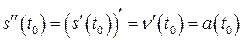 .
.
Формула Тейлора.
Нехай функція 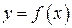 має в точці
має в точці 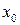 і деякому її околі похідні порядку п+1. Це означає, що функція
і деякому її околі похідні порядку п+1. Це означає, що функція 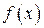 та її похідні до порядку п включно неперервні і диференційовні в цьому околі. Тоді справедлива формула Тейлора
та її похідні до порядку п включно неперервні і диференційовні в цьому околі. Тоді справедлива формула Тейлора
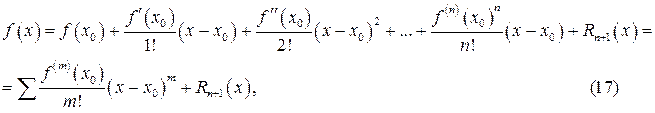 де
де 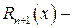 деякий залишковий член, причому
деякий залишковий член, причому 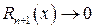 при
при 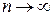 (0!=1 у формулі (17)).
(0!=1 у формулі (17)).
Отже, формула Тейлора надає можливість розкласти функцію 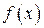 у степеневий ряд в околі деякої точки
у степеневий ряд в околі деякої точки 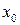 .
.
Зауваження. Формулою Маклорена називають формулу Тейлора (17) при 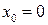 .
.
Приклад 1. Знайти 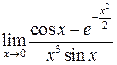 .
.
Маємо невизначеність 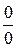 . Розкладемо функції
. Розкладемо функції 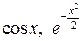 і
і 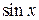 у ряд Маклорена з необхідною точністю:
у ряд Маклорена з необхідною точністю:
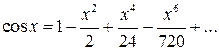
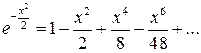
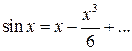
Тоді маємо:
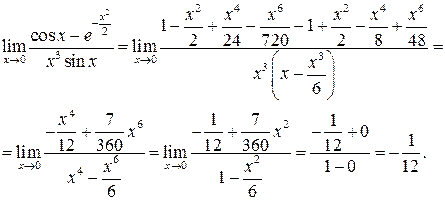
Приклад 2. Знайти 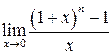 .
.
Маємо невизначеність 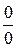 . Розкладемо функцію
. Розкладемо функцію 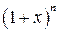 в ряд Маклорена:
в ряд Маклорена: 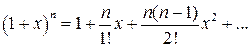 У результаті отримуємо:
У результаті отримуємо:
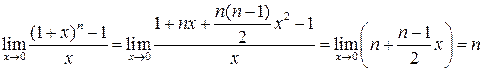 .
.
Дослідження функції на екстемум.
Асимптоти графіка функцій
Нехай функція 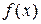 диференційована на інтервалі
диференційована на інтервалі 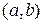 . Точка
. Точка 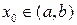 називається точкою екстремуму, якщо
називається точкою екстремуму, якщо 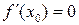 .
.
Точка екстемуму 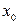 називається локальним мінімумом (максимумом), якщо
називається локальним мінімумом (максимумом), якщо 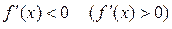 ліворуч від цієї точки і
ліворуч від цієї точки і 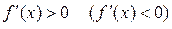 праворуч від цієї точки.
праворуч від цієї точки.
Крім того, у точці локального мінімуму (максимуму) справедливе співвідношення 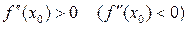 .
.
Точка 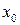 називається точкою перегину, якщо 1)
називається точкою перегину, якщо 1) 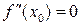 і 2)
і 2) 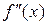 має різні знаки ліворуч і праворуч від точки
має різні знаки ліворуч і праворуч від точки 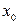 .
.
Приклад 1. Дослідити функцію 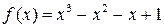 на екстремум.
на екстремум.
 Знаходимо похідну і прирівнюємо її нулю:
Знаходимо похідну і прирівнюємо її нулю: 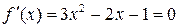 . Отже, точками екстремуму є
. Отже, точками екстремуму є 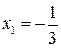 і
і 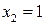 . Відмітивши їх на осі х (Рис. 3.1), дослідимо на її верхній частині знак похідної функції
. Відмітивши їх на осі х (Рис. 3.1), дослідимо на її верхній частині знак похідної функції 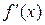 в околі цих точок екстремуму, а в її нижній частині – інтервали монотонності даної функції. У результаті маємо: на інтервалі (
в околі цих точок екстремуму, а в її нижній частині – інтервали монотонності даної функції. У результаті маємо: на інтервалі ( 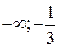 )
) 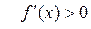 (функція
(функція 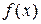 зростає), на інтервалі
зростає), на інтервалі 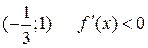 (функція
(функція 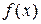 спадає), і, нарешті, на інтервалі
спадає), і, нарешті, на інтервалі 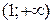
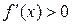 (функція
(функція 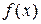 знову зростає). Це означає, що функція
знову зростає). Це означає, що функція 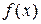 у точці
у точці 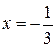 має локальний максимум
має локальний максимум 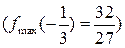 , а у точці х=1 – локальний мінімум
, а у точці х=1 – локальний мінімум 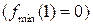 . Дійсно,
. Дійсно, 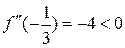 і
і 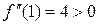 .
.
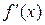 + max – min +
+ max – min +





 x
x
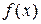
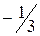 1
1
Рис. 3.1. Дослідження функції на екстремум


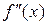 – +
– +
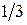 х
х
Рис. 3.2. Дослідження функції на перегин
Дослідимо, чи має дана функція точку перегину. Для цього знайдемо другу похідну і прирівняємо її до нуля: 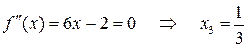 . З
. З
Рис. 3.2 видно, що 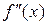 має різні знаки ліворуч і праворуч від точки
має різні знаки ліворуч і праворуч від точки 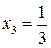 і, отже, дана точка є точкою перегину функції
і, отже, дана точка є точкою перегину функції 
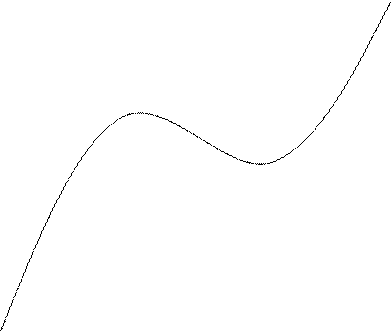
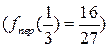 . Її графік наведено на Рис. 3.3.
. Її графік наведено на Рис. 3.3.
 |



 4 у
4 у
 |
2 
 |

 0
0 
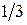 1 х
1 х
 |
 -2
-2
 | |||
 |
-4
-2 -1 0 1 2
Рис. 3.3. Графік функції 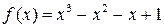
При дослідженні поведінки функції на нескінченності та поблизу точок розриву (невизначеності) часто виявляється, що графік функції як завгодно близько наближається до тієї чи іншої прямої. Такі прямі називаються асимптотами. Існують три види асимптот: вертикальні, горизонтальні і нахилені.
