Основные законы электрических цепей в комплексной форме

Основные законы электрических цепей справедливы для комплексных амплитуд, комплексов действующих значений, а также для амплитудных и действующих значений синусоидальных токов и напряжений.

Закон Ома. Общий вид закона Ома в комплексной форме: либо . В табл. 3.4 записан закон Ома для одноэлементного участка цепи.

Таблица 3.4 — Закон Ома в комплексной форме для одноэлементного участка цепи

Участок цепи	Запись закона Ома	Векторная диаграмма	Сдвиг фаз
Резистивный элемент			( )
Индуктивный элемент			( )
Емкостной элемент			( )

В табл. 3.5 приводится запись закона Ома при последовательном (рис.3.7) и параллельном (рис.3.8) соединении элементов R, L, C.

Таблица 3.5 — Закон Ома в комплексной форме для участка цепи с последовательным и параллельным соединением элементов R, L, C

Участок цепи	Запись закона Ома	Векторная диаграмма	Сдвиг фаз
Последо- вательная RLC-цепь			( ) индуктивный характер цепи
	( ) активный характер цепи
	( ) емкостной характер цепи
Параллельная RLC-цепь			( ) инд.хар. цепи
	( ) акт. хар. цепи
	( ) емк.хар. цепи

Первый закон Кирхгофа. Алгебраическая сумма комплексов токов, сходящихся в узле, равна нулю : .

Второй закон Кирхгофа. Алгебраическая сумма комплексов ЭДС, действующих в замкнутом контуре, равна сумме падений напряжений во всех ветвях контура: .

3.7 Соотношения между активными, реактивными и полными величинами (сопротивление, проводимость, напряжение, мощность)

Для запоминания соотношений между активными, реактивными и полными значениями 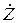, , 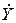, удобно воспользоваться их представлением в виде прямоугольных треугольников (табл.3.6).

Таблица 3.6 — Треугольники сопротивлений, проводимостей, напряжений, мощностей