Сызықтық алгебралық теңдеулер жүйесiн шешудің итерация
Дісі.
Сызықтық алгебралық теңдеулер жүйесiн шешудің Зейдель
Итерациясы әдісі.
Сызықтық алгебралық теңдеулер жүйесiн шешудің итерация
Дісі.
Сызықтық теңдеулер жүйесінде белгісіздер саны көп болған жағдайда жүйенің түбірлерін табу үшін жуықталған сандық әдістерді қолданған ыңғайлы.
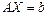(1)
сызықтық теңдеулер жүйесі берілсін және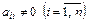 
деп үйғарайық Берілген (1) жүйені нормаль (келтірілген) жүйеге келтірейік
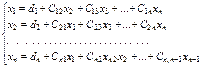(2)
мұндағы
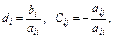егер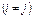 
;
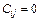, егер 
.
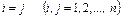Бастапқы жуықтау ретінде бос мүшелерді аламыз
.
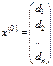Жалпы алғанда (2) жүйеден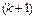 
-ші жуықтау келесі формулалар арқылы табылады
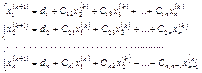(3)
Егер келесі шарттардың ең болмағанда біреуі орындалса
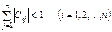(4)
немесе
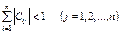. (5)
онда (3) итерация процесі бастапқы жуықтауды таңдауға тәуелсіз осы жүйенің жалғыз шешіміне жинақталады, яғни
.
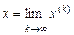Итерация процесін
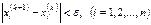(6)
болғанда тоқтатамыз, мұнда e>0 қандайда бір аз шама.