Условия прочности при прямом поперечном изгибе

Балки рассчитывают на прочность по наи­большим нормальным напряжениям, возникающим в их поперечных сечениях. При поперечном изгибе балок наряду с нормальными, как известно, возникают и касательные напряжения, но они в подавля­ющем большинстве случаев невелики и при расчетах на прочность не учитываются.

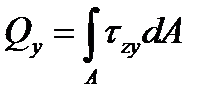
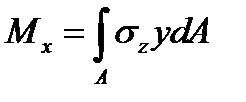
Расчет балок из пластичных материалов.

Прочность балки из пластичного материала обеспечена, если наибольшие по абсолютному значению нормальные напряжения, воз­никающие в опасном поперечном сечении, не превышают допускаемых. Для балки, поперечные размеры которой по всей длине постоянны (пока только такими балками и ограничимся), опасное сечение то, в котором возникает наибольший по модулю изгибающий момент.

Наибольшие нормальные напряжения возникают в точках опас­ного поперечного сечения, максимально удаленных от нейтральной оси. Будем называть эти точки опасными. 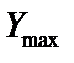– расстояние от опасной точки до нейтральной оси. Тогда получим условие проч­ности в виде

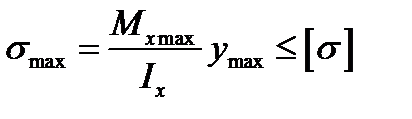(19.5)

где 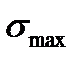– максимальное нормальное напряжение;

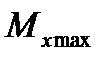– максимальный изгибающий момент;

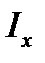– момент инерции относительно оси ОХ – осевой момент инерции;

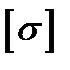– допускаемое напряжение, принимаемое при статическом нагружении таким же, как и в случае растяжения (сжатия) бруса из того же материала.

В случае если поперечное сечение балки симметрично отно­сительно нейтральной оси, оказывается возможным привести форму­лу (19.5) к более удобному виду. Для указанных сечений 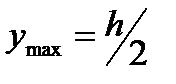гдеh – высота сечения (размер в направлении, перпен­дикулярном нейтральной оси), следовательно,

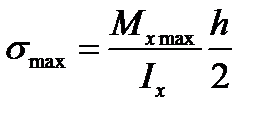
Разделим числитель и знаменатель этого выражения :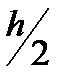

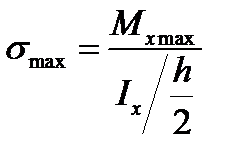
Введем обозначение

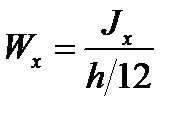
и получим окончательное условие прочности в следующем виде:

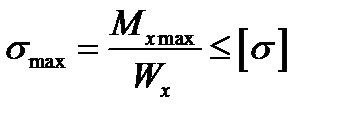(19.6)

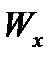– осевой момент сопротивления, или момент сопротивления при изгибе.

Момент сопротивления– это геометрическая характеристика, прочности бруса, работающего на прямой изгиб. Действительно, чем больше момент сопротивления, тем меньше напряжения, возника­ющие в поперечном сечении балки при данной нагрузке.

Формула представляет собой зависимость для проверочного расчета.

Значения моментов сопротивления прокатных профилей (двутавров и швеллеров) приведены в таблицах соответствующих ГОСТов.

Моменты сопротивления круга, кольца и прямоугольника:

а) круг

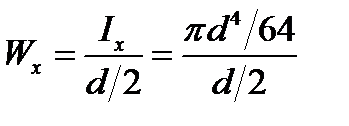
или

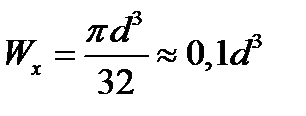(19.7)

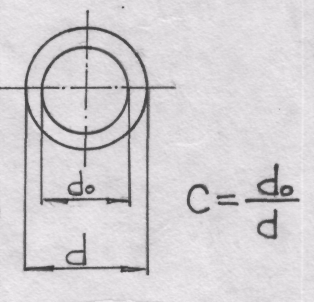
б)кольцо (рис. 19.11)

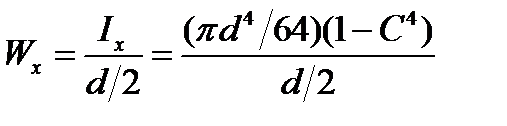
или

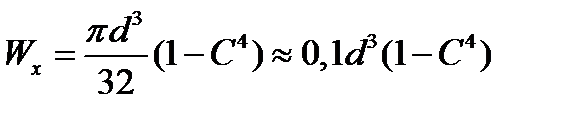(19.8)

в) прямоугольник

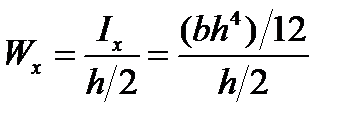
или

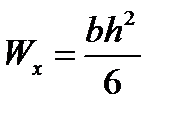(19.9)

h – сторона прямоугольника, перпендикулярная оси, относительно которой вычисляется момент сопротивления.

Из приведенных примеров следует, что сечение надо распола­гать таким образом, чтобы силовая линия совпадала с той из главных осей, относительно которой момент инерции минимален, или, что то же самое, так, чтобы ось, относительно которой мо­мент инерции максимален, была нейтральной осью сечения. Более кратко это можно сформулировать так: следует стремиться к тому, чтобы изгиб бруса происходил в плоскости его наибольшей жесткости.

46. Схема расчёта на прочность при изгибе, условия прочности при изгибе.

Расчеты на жесткость при изгибе.

В ряде случаев работающие на изгиб элементы машиност­роительных и строительных конструкций должны быть рассчитаны не только на прочность, но и на жесткость. К деталям, рассчитываемым на жест­кость, относятся, в частности, валызубчатых и червячных передач и многие части металлорежущих станков.

Расчет на жесткость элемента конструкции, имеющего форму бруса, заключается в определении наибольших перемещений его по­перечных сечений и сопоставлении их с допускаемыми, зависящими от назначения и условий эксплуатации данного элемента.

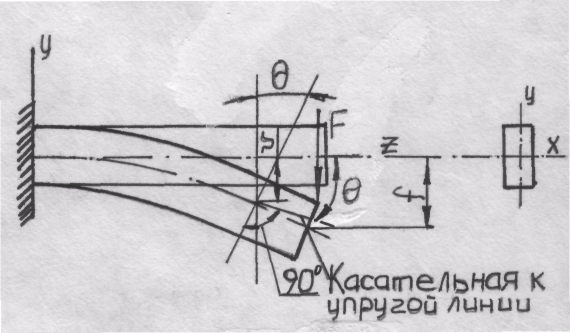
Рассмотрим простую консоль, нагруженную на свободном конце силой F, линия действия которой совпадает с одной из главных осей поперечного сечения балки (рис. 19.12).

При деформации балки центры тяжести ее поперечных сечений получают линейные перемещения, а сами сечения поворачиваются вокруг своих нейтральных осей. Допущение о малости перемещений позволяет считать, что направления линейных перемещений перпен­дикулярны продольной оси недеформированного бруса. Эти перемещения принято называть прогибами. Прогиб произвольного сечения обозначим 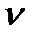, а наибольший прогиб –стрелу прогиба– f. Геометрическое место центров тяжести поперечных сечений деформиро­ванного бруса, т.е. ось изогнутого бруса, условно называют изогнутой осью, или чаще упругой линией.

Угол поворота 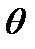поперечного сечения равен углу между касательной к упругой линии в данной точке и осью недеформиро­ванного бруса.

Вывод: ордината упругой линии и угол наклона касательной, проведенной к ней в данной точке, полностью определяют линейное и угловое перемещения соответствующего поперечного сечения бал­ки.

В большинстве случаев условие жесткости выражается нера­венством

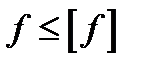(19.10)

т.е. максимальный прогиб (стрела прогиба f) не должен превы­шать допускаемого 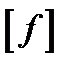. Значение допускаемого прогиба зависит от назначения и условий работы рассчитываемой конструкции и ко­леблется в широких пределах. Обычно допускаемую стрелу прогиба указывают в долях пролета (межопорного расстояния l) балки. Например, для ручных грузоподъемных кранов 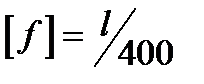, для электрических 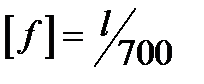, для валов и шпинделей металло­режущих станков 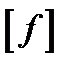= 0.0005...0.0010l.

Для обеспечения нормальной работы подшипников скольжения и роликовых подшипников качения иногда ставится дополнительное условие жесткости – ограничение угла поворота опорных сечений:

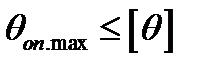(19.11)

При этом допускаемый угол поворота составляет в среднем 0,001 рад.