Дәріс сабағы. Кеңістіктегі жазықтық пен түзулер

Координаттар жүйесінің түрлері.Аналитикалық геометрия геометриялық бейнелерді координаттар методы негізінде алгебраның күшімен зерттейтін математиканың бір саласы.

Аналитикалық геометрияда есеп алдын-ала таңдалған координаттар жүйесіне байланысты шығарылады. Координаттар жүйесі дегеніміз нүктенің кеңістіктегі (жазықтықтағы, түзудің бойындағы) орнын анықтау үшін қажетті және жеткілікті шарттардың жиыны. Координаттар жүйесі бас нүктеден және базистік векторлардан тұрады. Базистік векторлар өздері орналасқан түзулердің бойында есептеудің әрі оң бағытын, әрі өлшем бірлігін анықтайды. Кейін, осылайша оң бағыттары анықталған түзулерді өстер деп атайды және әр өске дербес ат тағылады (абсциссалар өсі, ординаталар өсі, аппликаталар өсі). Базистік векторларының ұзындықтары әртүрлі жүйе аффиндік координаттар жүйесі деп аталады. Базистік векторларының ұзындықтары бірдей жүйе декарт жүйесі деп аталады. Базистік векторлары қос-қостан өзара перпендикуляр жүйе тікбұрышты деп, басқа жағдайда қиғаш бұрышты деп аталады. Сонымен, тікбұрышты аффин немесе декарт жүйелері, қиғаш бұрышты аффин немесе декарт жүйелері болады. Ең қарапайымы, есеп шығаруға қолайлысы тікбұрышты декарттық координаттар жүйесі. Декарт координат жүйесінен басқа полярлық координат жүйесі де бар.

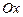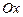Жазықтықтағы полярлық координаттар дегеніміз тұрақты О нүктесі мен сәулесіне салыстырмалы түрде М нүктесінің орнын анықтайтын екі сан (1-сурет). Бұл екі санның декарт координаттарынан айырмашылығы олардың әртекті шамалар екендігінде: - ұзындық; -бұрыш. О нүкте-полюс, -полярлық өс, ал - поляр радиусы деп аталады. Поляр радиусы дегеніміз полюстен берілген нүктеге дейінгі арақашықтық, ал поляр радиусымен поляр өсі арасындағы бұрыш полярлық бұрыш деп аталады, . Егер болса, онда бұрышын сағат тіліне қарама-қарсы бағытта, ал егер болса, онда бұрышын сағат тіліне бағыттас бағытта аламыз. -кез келген нақты сан.

Тік бұрышты және поляр координат жүйесінің арасындағы байланыс мынадай теңдіктермен анықталады: . , .

1-сурет 2-сурет

Тік бұрышты декарт координат жүйесін түрлендіру. 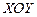координат жүйесін бас нүктесі болатын нүктеге параллель көшіру нәтижесінде координат жүйесін аламыз. Осы жаңа және ескі координат жүйелерінде берілген нүктенің координаттарының арасындағы байланыс мына формуламен анықталады:

Координат жүйесін бұрышқа бұруда ескі және жаңа координат жүйелерінің арасындағы байланыс мына формуламен анықталады:

Жазықтықтағы түзудің әртүрлі теңдеулері.

1. Берілген бір нүктеден өтіп берілген векторға перпендикуляр түзудің теңдеуі: . .Түзу бойынан еркімізше нүктесін алып, векторын қарастырамыз. , -нормаль вектор (2-сурет).

2. Түзудің жалпы теңдеуі: . 1-нші теңдеудегі деп белгілесек, жалпы теңдеуі шығады. . , ал болады.

3. Түзудің канондық теңдеуі: . , яғни мен - коллинеар, ендеше, кординаттары пропорционал. - бағыттауыш вектор (2-сурет).

4. Екі нүктеден өтетін түзу теңдеуі: . (2-сурет).

5. Түзудің параметрлік теңдеуі. . 3-тегі қатынасты деп белгілеп, ол қатынастардан х пен у-ті табамыз.

6. бірлік векторы түзуі сияқты 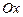өсімен бұрышын жасайды, бағыттауыш векторы ретінде осы бірлік векторды аламыз және екендігін ескерсек, . Бұдан, , . Ендеше, - белгілі бір бағытпен берілген нүктеден өтетін түзу теңдеуі. Бұл теңдеу түзулер шоғы теңдеуі деп те аталады, -шоқтың центрі (2-сурет).

7. Түзу Оу өсін нүктесінде қияды десек, яғни болса, онда - бұрыштық коэффициентпен берілген түзу теңдеуі. 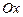өсіне перпендикуляр түзудің бұрыштық коэффициенті болмайды. -бұрыштық биссектрисалар теңдеуі.

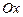8. Түзудің кесінді теңдеуі: . - түзудің сәйкес , Оу өстерден қиятын кесінділерінің ұзындықтары. теңдеуінің екі жағын – С-ға бөліп, деп белгілесек, түзудің кесінді теңдеуін аламыз.

9. Түзудің полярлық теңдеуі: . . р – түзудің О – полюстен қашықтығы, - р-нің полярлық өспен жасайтын бұрышы, векторының полярлық өспен жасайтын бұрышы. Түзудің полярлық теңдеуінен: . Бұдан, тікбұрышты декарт пен полярлық координаттар жүйелері арасындағы байланысты ескерсек, түзудің нормаль теңдеуін аламыз. Түзудің нормаль теңдеуі: . р - түзудің О нүктесінен ара қашықтығы, - р-нің Ох өсімен жасайтын бұрышы. Түзудің жалпы теңдеуін нормаль теңдеуге келтіру үшін жалпы теңдеуді нормалаушы көбейткіш деп аталатын санына көбейту керек, . Оның таңбасы С коэффициентінің таңбасына қарама-қарсы етіп алынады.

нүктесінен түзуге дейінгі ара қашықтық мына формуламен табылады: .

Екі түзу арасындағы бұрыш мына формулалармен табылады:

;

Екі түзулердің параллельдік белгісі: немесе .

Екі түзудің перпендикулярлық белгісі: немесе .

Мысал. нүктесінен өтетін және Ох өсімен бұрыш жасайтын түзу теңдеуін табу керек.

Шешуі: . формуласы бойынша . Бұдан: .

2. нүктесінен өтетін және түзуіне перпендикуляр болатын түзу теңдеуін табу керек.

Шешуі. Берілген түзу теңдеуінен . Іздеп отырған түзудің бұрыштық коэффициенті . Ендеше, . Бұдан: .

Кеңістіктегі жазықтық. теңдеуі кеңістігінде қандай-да бір бетті анықтайды.Кез келген жазықтық 1-нші ретті бетке жатады. Ол мынандай түрдегі теңдеулермен беріледі:

1. Бір нүктеден өтіп берілген векторға перпендикуляр болатын жазықтық теңдеуі: 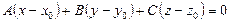. Жазықтыққа перпендикуляр векторды нормаль вектор деп атайды және оны деп белгілейді, ол жазықтықтың координат жүйесіне қатысты кеңістіктегі орнын (бағытын) анықтайды: Жазықтықтан М нүктесін қалай алсақ та, болады, сондықтан (1-сурет)

2. Жазықтықтың жалпы теңдеуі: 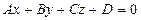, мұндағы А, В, С- коэффи-циенттерінің ең болмағанда біреуі нөлге тең емес және , .

3. Бір түзудің бойында жатпайтын үш нүкте арқылы өтетін жазықтықтың теңдеуі:

Кеңістікте жатқан кез келген нүкте іздестіріп отырған жазықтықта жатуы үшін , , -векторларының компланарлығы қажетті әрі жеткілікті: . Бұл көбейтіндіні координаттық түрде жазсақ, жоғарыдағы теңдеуді аламыз.

4. Жазықтықтың кесінді теңдеуі: , мұндағы , олар сәйкес өстерінің бойынан жазықтықтың қиятын кесінділерінің ұзындықтары.

5. Жазықтықтың нормаль теңдеуі: , мұндағы - координат бас нүктесінен жазықтыққа түсірілген перпендикулярмен бағыттас бірлік вектордың координаттары: , р-осы перпендикулярдың ұзындығы.

Жазықтықтың жалпы теңдеуін нормаль түрдегі теңдеуге келтіру үшін оны нормаль көбейткішке көбейтеміз: . Осы -санының таңбасы -коэффициентінің таңбасына қарама-қарсы алынады.

Екі жазықтық арасындағы бұрыш деп олар құрайтын екіжақты бұрыштардың біреуін айтады. Жазықтықтардың нормаль векторларының арасындағы бұрыш осы сыбайлас екіжақты бұрыштардың біреуіне тең болады.

а) Екі жазықтықтың параллельдік белгісі:

б) Екі жазықтық перпендикулярлық белгісі:

.

Берілген нүктеден жазықтығына дейінгі арақашықтық мына формуламен табылады: .

1-сурет 2-сурет

Кеңістіктегі түзу.Кеңістіктегі түзудің әртүрлі теңдеулері.

1) Түзудің векторлық-параметрлік теңдеуі: , мұндағы - радиус-векторлар, - бағыттауыш векторы, -параметр (2-сурет).

2) , бұл теңдіктер түзудің параметрлік теңдеуі деп аталады.

3) теңдеуді кеңістіктегі кез келген нүктеден өтіп бағыттауыш векторымен берілген түзудің ықшам (канонды) теңдеуі деп атайды.

Ескерту. Теңдеудегі бөлімдердің біреуінің нөлге айналуы оған сәйкес алымның да нөлге айналуын білдіреді.

Мысалы, теңдеуі нүктесінен өтіп өсіне перпендикуляр ( векторының өсіндегі проекциясы, яғни координатасы 0-ге тең) түзуді анықтайды. Бұл түзудің жазықтығында жататындығын білдіреді, сондықтан түзудің кез келген нүктесі үшін болады.

4) түзуі нүктелері арқылы өтетін болсын. деп алсақ, екі нүктеден өтетін түзу теңдеуін табамыз: (2-сурет).

5) Кеңістіктегі түзуді екі жазықтықтың қиылысу сызығы ретінде қарастыруға болады және оны түзудің жалпы теңдеуі дейді:

, мұндағы .

Түзудің жалпы теңдеуінен ықшам теңдеуін алу үшін түзу бойынан қандай да бір нүктесін табу керек, координаттардың біреуіне кез келген мән бере отырып (мысалы, ), оны жүйенің шешімі ретінде анықтаймыз. Ал түзуі векторларына перпендикуляр болғандықтан, - бағыттауыш векторы векторларының векторлық көбейтіндісі ретінде анықталады:

.

Ескерту. Екі нүктені жүйеден тауып, (4) формуланы пайдаланып жалпы теңдеуден ықшам теңдеуді оңай табуға болады.

Екі түзу арасындағы бұрыш ретінде олардың бағыттауыш векторларының арасындағы сыбайлас бұрыштардың біреуі алынады: .

Ендеше, .

Перпендикулярлық белгісі: .

Параллельдік белгісі: (коллинеар) .

Нүктеден түзуге дейінгі қашықтық. Кеңістікте түзуден тыс жатқан нүктесінен осы түзуге дейінгі қашықтық деп, нүктесінен түзуіне түсірілген перпендикулярдың ұзындығын айтады. : , , . . , яғни қашықтық - векторлары арқылы тұрғызылған параллелограммның биіктігі ретінде анықталады.

Кеңістіктегі түзу мен жазықтық

Кеістіктегі түзу мен жазықтық арасындағы бұрыш деп түзу мен оның жазықтықтағы проекциясы арасындағы бұрышты айтады:

а) Параллельдік шарты: .

б) Перпендикулярлық шарты: .

Түзу мен жазықтықтың қиылысу нүктесін табу үшін олардың теңдеулерін біріктіріп шешеміз.

Мысалдар: 1. нүктесінен өтетін және YOZ жазықтығына паралллель болатын жазықтықтың теңдуін табыңыз.

Шешуі: YOZ жазықтығына параллель жазықтықтың теңдеуі болады. Есеп шарты бойынша 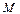нүктесі ізделінді жазықтықтың бойында жатыр, сондықтан оның координаттары жазықтық теңдеуін қанағаттандырады, яғни немесе -ның орнына -2А-ны қоямыз. Сонда немесе . Бұл іздеп отырған жазықтық теңдеуі болады.

2. нүтесінен жазықтығына дейінгі қашықтықты табыңыз.

Шешуі: , .

Бақылау сұрақтары:

1. Кеңістіктегі түзудің бағыттауыш векторы дегеніміз не?

2. Жазықтықтың жалпы теңдеуін жазыңыз. Ондағы коэффициенттер нені білдіреді?

3. Нүктеден жазықтыққа дейінгі қашықтықты қалай есептейді?

Негізгі әдебиет: [4], 4 тарау, § 4.1-4.16 (183-217 беттер).

Қосымша әдебиет: [17], 2 тарау, § 2.17-2.21 (103-118 беттер).