Глава 3. Статистическая физика и её применение к идеальному газу

В физике строго научное развитие молекулярной теории началось примерно со второй половины 19 века главным образом благодаря трудам Клаузиуса, Максвелла и Больцмана, в которых были заложены основы молекулярно – кинетической теории, которая была сформулирована во введении. В дальнейшем мы будем рассматривать молекулярно – кинетическую теорию идеального газа.

С точки зрения статистической физики под идеальным газом понимают газ, обладающий следующими свойствами:

а) молекулы газа представляют упругие шарики пренебрежимо маленького размера;

б) сила притяжения между молекулами пренебрежимо мала:

в) сила отталкивания между молекулами проявляется только в момент взаимостолкновений;

Г) число взаимостолкновений между молекулами пренебрежимо мало по сравнению с числом их ударов об стенки сосудов.

Давление газа с точки зрения молекулярно – кинетической теории

Основная задача статистической теории физики – это установление связи между макроскопическими параметрами (температура, давление и т. д.) и микроскопическими параметрами вещества (скорости, кинетические энергии, импульсы молекул).

Давление газа на стенку есть результат ударов молекул газа об эту стенку. При каждом ударе молекулы газа действует на стенку с определённой силой. Обратно направленная сила, с которой действует на молекулу стенка сосуда, заставляет молекулу отражаться от стенки. Если бы в сосуде содержалось всего несколько молекул, то их удары следовали бы друг за другом редко и беспорядочно, и нельзя было бы говорить ни о какой определённой силе давления, действующей на стенку. Мы имели бы дело с отдельными практически мгновенными бесконечно малыми толчками, которым время от времени подвергалась бы стенка. Если же число молекул в сосуде очень велико, то будет велико и число ударов их о стенку сосуда. Удары станут следовать непрерывно друг за другом. Одновременно о стенку сосуда будет ударяться громадное количество молекул. Бесконечно малые силы отдельных ударов складываются в конечную и почти постоянную силу, действующую на стенку. Эта сила, усреднённая по времени и есть давление газа. Вычислим давление газа на стенку сосуда.

Пусть некоторая молекула движется в сосуде со скоростью 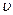. Как бы не была направлена эта скорость, её всегда можно разложить на три составляющие, из которых одна перпендикулярна стенке сосуда, а два других параллельны ей. Нас интересует только первая из них, так как при ударе только она и может изменяться.

Предположим, что в сосуде объёмом V, кубической формы, находиться N молекул, тогда на единицу объёма приходиться n=N/VV число молекул. Величину n называют численной плотностью газа или концентрацией. Рассмотрим удары молекул на заштрихованную площадку, перпендикулярную оси X. При ударе об эту стенку молекулы массой m, будет меняться только перпендикулярная к этой стенке составляющая импульса m . После соударения со стенкой, которое будем считать упругим, молекула отразиться от стенки под углом равным углу падения, при этом импульс молекулы станет равным -m . Значит, изменение импульса молекулы станет равным 2m _. Пусть на стенку площадью DS за время Dt попадает N_X молекул с одинаковыми скоростями 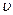, причём Х - составляющая импульса каждой молекулы равна m . Тогда общее изменение импульса всех этих молекул за время Dt равно DP_x=2m N_x. Согласно II закону Ньютона сила, действующая на стенку за счёт удара молекул, будет равна

. (3.1)

Остаётся вычислить число молекул N_x, попадающих за время Dt на площадку DS. За время Dt до стенки DS дойдут только те молекулы, которые находятся не далее чем на расстоянии Dt от неё, т.е. молекулы которые заключены в объёме параллелепипеда с площадью основания DS и с высотой Dt. Объём такого параллелепипеда равен DtDS. Если в единице объёма содержится n молекул газа то, число молекул в указанном объёме равно n DtDS. Из этого числа только половина попадёт на площадку DS. Остальные в силу полной беспорядочности молекулярных движений движутся в противоположенном направлении и не попадают на стенку, значит, за время Dt о площадку ударятся число молекул

. (3.2)

Тогда сила испытываемая площадью DS от ударов всех N_X молекул согласно (3.1) равно

.

Значит, давление на стенку равно

. (3.3)

При получении формулы (3.3) мы предположили, что все молекулы имеют одинаковую скорость. В действительности из-за хаотичности движений молекул и их столкновений молекулы имеют различные скорости. Вычислим теперь давление газа с учётом этого. Для этого введём понятие средней скорости молекул. Если в сосуде имеется N молекул соответственно со скоростями то средняя скорость этих молекул будет равна

. (3.4)

К определению средней скорости можно подойти и по-другому. Пусть из N молекул, находящихся в сосуде, N₁ имеет скорость , N₂ – скорость и т. д. N_k – . Тогда среднюю скорость молекул можно определить следующим образом

. (3.5)

Если разбить N_X молекул, попадающих на стенку DS на k-групп со скоростями , тогда согласно формуле (3.3)

, (3.6)

где n_i – концентрация молекул имеющих x-компоненту скорости 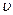_ix. Перепишем (3.6) в виде

. (3.7)

Используя (3.5) получим следующее выражение для давления

, (3.8)

где - среднее значение квадрата x компоненты скорости. Поскольку и ввиду хаотичности движений молекул имеем . Тогда

. (3.9)

Формулу (3.9) перепишем в виде

. (3.10)

Величина представляет собой среднюю кинетическую энергию одной молекулы газа. Уравнение (3.10) называют основным уравнением кинетической теории газов. Оно устанавливает связь между молекулярными величинами (масса и скорость молекул) и давлением, характеризующим газ как целое, и непосредственно измеряемое на опыте.

Важно подчеркнуть, что давление газа определяется средней кинетической энергией его молекул. Это значит, что давление газа – это величина, органически связанная с тем, что газ состоит из большого числа молекул. Не имеет, поэтому смысла говорить, например, о давлении, создаваемом одной или немногими молекулами. О таких величинах, которые имеют смысл только для систем, содержащих очень много частиц, говорят, что они имеют статистический характер.