Пример 1. Определение моментов инерции сечения, имеющего одну ось симметрии
Условие задачи
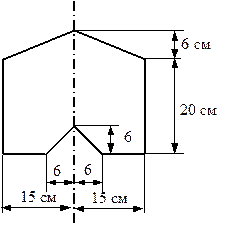 Рис. 5.17. Фигура с одной осью симметрии Рис. 5.17. Фигура с одной осью симметрии |
Сечение стержня представляющее собой фигуру, обладающую одной осью симметрии, показано на рис. 5.17. Требуется найти моменты инерции этой фигуры относительно главных центральных осей.
Решение
Ось 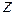 – ось симметрии фигуры (рис. 5.18) – является главной осью инерции. Найдем положение второй главной центральной оси, определив положение центра тяжести фигуры. Очевидно, что центр тяжести лежит на оси симметрии, поэтому найдем только координату
– ось симметрии фигуры (рис. 5.18) – является главной осью инерции. Найдем положение второй главной центральной оси, определив положение центра тяжести фигуры. Очевидно, что центр тяжести лежит на оси симметрии, поэтому найдем только координату 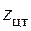 по последней из формул (5.15). Разобьем сложную фигуру на составляющие простые: две пары прямоугольных треугольников I , III и прямоугольник II (см. рис. 5.18). Площадь фигуры
по последней из формул (5.15). Разобьем сложную фигуру на составляющие простые: две пары прямоугольных треугольников I , III и прямоугольник II (см. рис. 5.18). Площадь фигуры
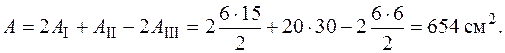
Для определения статического момента выберем вспомогательную ось  , проходящую через центр тяжести прямоугольника II. В этом случае статический момент фигуры II равен нулю. Чтобы найти статические моменты треугольников, умножаем площадь фигуры на координату ее центра тяжести в системе
, проходящую через центр тяжести прямоугольника II. В этом случае статический момент фигуры II равен нулю. Чтобы найти статические моменты треугольников, умножаем площадь фигуры на координату ее центра тяжести в системе 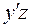 :
:
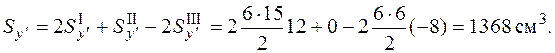
Тогда по (5.15)
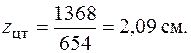
Откладываем эту координату и проводим через центр тяжести (точку С на рис. 5.18) главную центральную ось 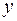 .
.
Найдем моменты инерции всей фигуры относительно осей 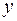 и
и 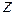 , складывая (или вычитая) моменты инерции составляющих фигур:
, складывая (или вычитая) моменты инерции составляющих фигур:
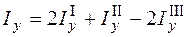 ;
;
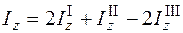 .
.
Для определения момента инерции каждой из фигур I, II и Ш используем формулы изменения моментов инерций при параллельном переносе осей (5.16), (5.17). Моменты инерции прямоугольника II и треугольников I и Ш относительно собственных центральных осей  (см. рис. 5.18) находим по формулам (5.26), (5.28). Тогда
(см. рис. 5.18) находим по формулам (5.26), (5.28). Тогда
 Рис. 5.18. К определению моментов инерции симметричной фигуры Рис. 5.18. К определению моментов инерции симметричной фигуры |
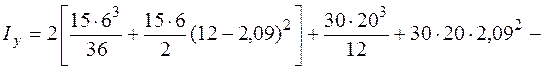
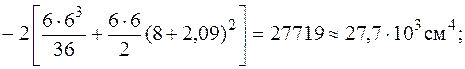
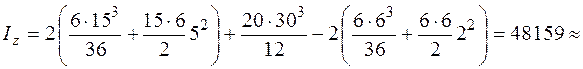
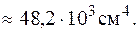
В заключение вычислим радиусы инерции относительно главных центральных осей по формулам (5.10) и построим эллипс инерции.
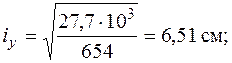
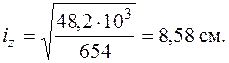
Эллипс инерции показан на рис. 5.18.
Пример 2. Определение моментов инерции
Несимметричного сечения
Условие задачи
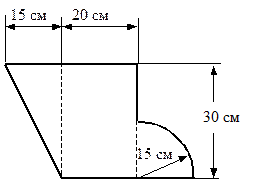 Рис. 5.19. Несимметричная фигура Рис. 5.19. Несимметричная фигура |
Сечение стержня представляет собой несимметричную фигуру, показанную на рис. 5.19. Требуется найти положение главных центральных осей инерции фигуры и моменты инерции относительно этих осей.
Решение
Найдем положение центра тяжести фигуры по формулам (5.15). Разобьем фигуру на три простые: треугольник I, прямоугольник II и квадрант круга Ш. Площадь всей фигуры
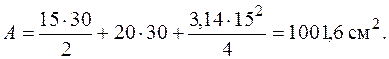
Для определения статических моментов выберем вспомогательные оси 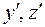 , проходящие через центр тяжести прямоугольника II (рис. 5.20). Статический момент каждой фигуры равен площади фигуры, умноженной на координату центра тяжести этой фигуры в системе координат
, проходящие через центр тяжести прямоугольника II (рис. 5.20). Статический момент каждой фигуры равен площади фигуры, умноженной на координату центра тяжести этой фигуры в системе координат 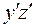 . Суммарные статические моменты
. Суммарные статические моменты
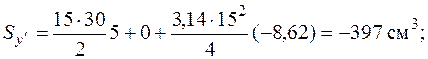
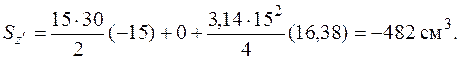
Координаты центра тяжести
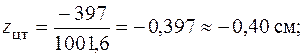
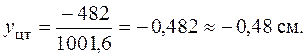
отложены на рис. 5.20.
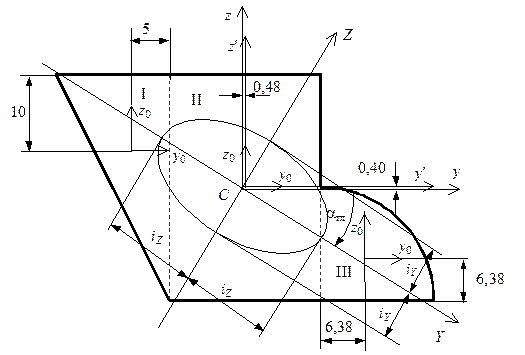 Рис. 5.20. К определению моментов инерции несимметричной фигуры Рис. 5.20. К определению моментов инерции несимметричной фигуры |
Проведем через центр тяжести центральные оси 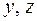 (см. рис. 5.20) и найдем моменты инерции относительно этих осей, как сумму моментов инерций простых фигур, составляющих заданную фигуру. Для определения моментов инерции простых фигур I, II и Ш используем формулы (5.16)–(5.18). Моменты инерции относительно собственных осей
(см. рис. 5.20) и найдем моменты инерции относительно этих осей, как сумму моментов инерций простых фигур, составляющих заданную фигуру. Для определения моментов инерции простых фигур I, II и Ш используем формулы (5.16)–(5.18). Моменты инерции относительно собственных осей  прямоугольника, треугольника и квадранта круга вычисляем по формулам (5.26), (5.28) и (5.29).
прямоугольника, треугольника и квадранта круга вычисляем по формулам (5.26), (5.28) и (5.29).
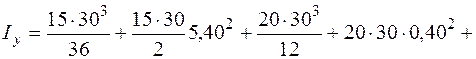
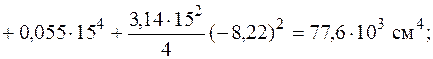
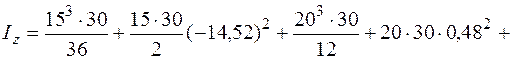
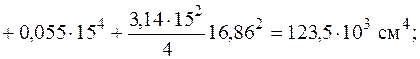
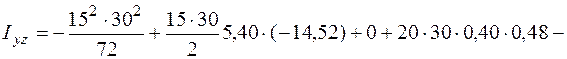
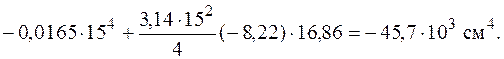
Теперь найдем положение главных осей инерции. Угол, на который надо повернуть ось 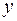 , чтобы она стала главной осью, определяем по формуле (5.23):
, чтобы она стала главной осью, определяем по формуле (5.23):
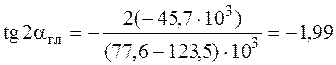 ;
;
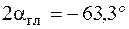 ;
; 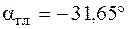 .
.
В соответствии с правилом знаков откладываем отрицательный угол  по часовой стрелке и проводим главные центральные оси инерции
по часовой стрелке и проводим главные центральные оси инерции  (см. рис. 5.20). Вычислим моменты инерции относительно этих осей по формуле (5.24):
(см. рис. 5.20). Вычислим моменты инерции относительно этих осей по формуле (5.24):
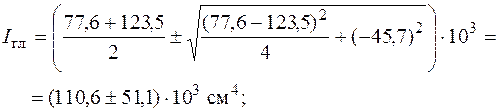
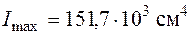 ;
; 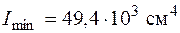 .
.
Для проверки вычислений удобно использовать следующее свойство: сумма моментов инерций относительно двух любых пар ортогональных осей есть величина постоянная. Тогда должно быть
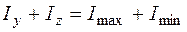 .
.
В нашем примере 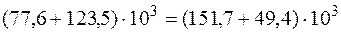 .
.
Чтобы выяснить, какой момент инерции – максимальный или минимальный – соответствует оси  , исследуем знак второй производной функции
, исследуем знак второй производной функции  по (5.25).
по (5.25).
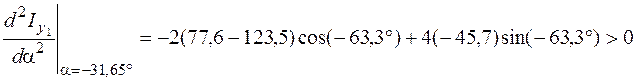 .
.
Положительный знак второй производной означает, что оси  соответствует минимальное значение момента инерции, т. е.
соответствует минимальное значение момента инерции, т. е.
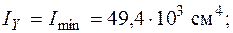
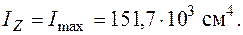
Найдем радиусы инерции относительно главных центральных осей по (5.10) и построим эллипс инерции.
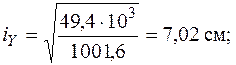
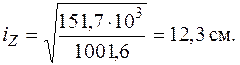
Эллипс инерции показан на рис. 5.20. Видно, что эллипс вытянут в том направлении, в котором вытянута фигура.
5.2.2. Определение грузоподъемности жесткого стержня моносимметричного сечения при внецентренном
растяжении-сжатии (задача № 29)
Условие задачи
Жесткий стержень загружен двумя силами – растягивающей и сжимающей (рис. 5.21). Стержень выполнен из хрупкого материала с характеристиками 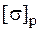 и
и 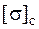 . Сечение стержня симметрично и имеет форму и размеры, соответствующие рис. 5.17. Требуется:
. Сечение стержня симметрично и имеет форму и размеры, соответствующие рис. 5.17. Требуется:
1) найти допускаемую нагрузку на стержень из условия прочности, если отношение сжимающей и растягивающей сил 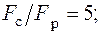
2) построить ядро сечения.
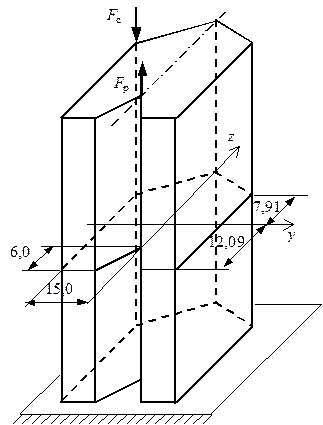 Рис. 5.21. Стержень, подверженный растяжению-сжатию двумя силами Рис. 5.21. Стержень, подверженный растяжению-сжатию двумя силами |
Решение
Положение главных центральных осей инерции и моменты инерции относительно этих осей заданного сечения найдены ранее в п. 5.2.1 (пример 1). Найдем внутренние усилия в произвольном сечении стержня:
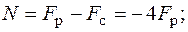
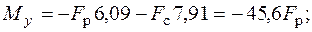
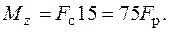
Для определения положения опасных точек построим нейтральную линию. Уравнение нейтральной линии (5.2) в данной задаче имеет вид
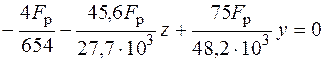 ,
,
или
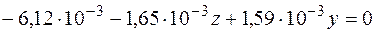 .
.
Отсюда найдем отрезки, отсекаемые нейтральной линией на осях 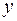 и
и 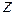 . Если
. Если 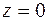 , то
, то
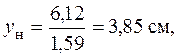
и, если 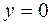 , то
, то
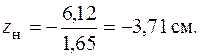
 Рис. 5.22. Эпюра напряжений от действия сил Fр и Fс и ядро сечения Рис. 5.22. Эпюра напряжений от действия сил Fр и Fс и ядро сечения |
Нейтральная линия показана на рис. 5.22. Проведем касательные к контуру сечения, параллельные нейтральной линии. Опасными являются точки 1 и 1¢ (см. рис. 5.22), наиболее отдаленные от нейтральной линии. Для хрупкого материала более опасной является точка с максимальными растягивающими напряжениями, т. е. точка 1. Найдем напряжение в этой точке, подставляя в формулу (5.1) координаты точки 1:
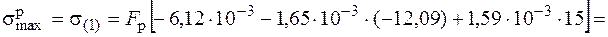
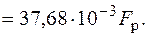
Условие прочности в точке 1 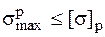 , или
, или
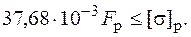
Отсюда можно найти допускаемое значение нагрузки[8]. В заключение необходимо убедиться в том, что и в точке 1¢, которая в данном примере дальше удалена от нейтральной оси, чем точка 1, и в которой действуют сжимающие напряжения, условие прочности тоже выполняется, т. е.
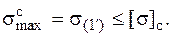
Теперь построим ядро сечения. Поместим полюсы во внешних угловых точках сечения. Учитывая симметрию сечения, достаточно расположить полюсы в трех точках: 1, 2 и 3 (см. рис. 5.22). Подставляя в формулы (5.12) координаты полюсов, найдем отрезки, отсекаемые нейтральными линиями на осях 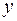 и
и 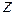 . Если полюс находится в точке 1, то его координаты
. Если полюс находится в точке 1, то его координаты 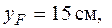
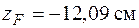 и
и
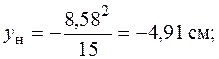
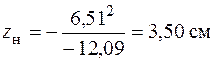 .
.
Нейтральная линия 1–1, соответствующая полюсу в точке 1, показана на рис. 5.22. Аналогично строим нейтральные линии 2–2 и 3–3, соответствующие полюсам 2 и 3. При построении нейтральной линии следите за тем, чтобы она проходила в квадранте, противоположном тому, в котором находится полюс. Область, заштрихованная на рис. 5.22, является ядром сечения. Для контроля на рис. 5.22 показан эллипс инерции. Ядро сечения должно находиться внутри эллипса инерции, нигде не пересекая его.
5.2.3. Определение грузоподъемности внецентренно сжатых жестких стержней несимметричных сечений (задачи № 30, 31)
Условие задачи
Стержень несимметричного сечения сжимается силой, приложенной в точке А (рис. 5.23). Поперечное сечение имеет форму и размеры, показанные на рис. 5.19. Материал стержня – хрупкий. Требуется:
1) найти допускаемую нагрузку, удовлетворяющую условию прочности;
2) построить ядро сечения.
Решение
Прежде всего надо определить моменты и радиусы инерции поперечного сечения относительно главных центральных осей. Эта часть решения задачи приведена в примере 2 п. 5.2.1. На рис. 5.23 показаны главные центральные оси инерции сечения  ,
,  , положение которых найдено ранее. В системе центральных осей
, положение которых найдено ранее. В системе центральных осей 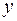 ,
, 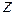 (рис. 5.24) координаты точки приложения силы А
(рис. 5.24) координаты точки приложения силы А 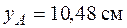 ,
, 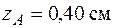 . Вычислим координаты точки А в системе главных центральных осей по формулам (5.19).
. Вычислим координаты точки А в системе главных центральных осей по формулам (5.19).
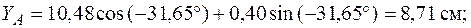
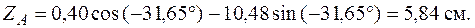
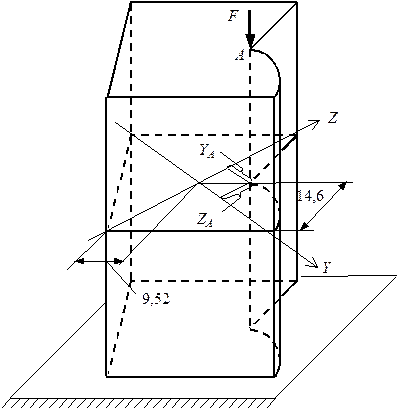 Рис. 5.23. Стержень, сжатый силой F Рис. 5.23. Стержень, сжатый силой F |
Найденные координаты рекомендуем проверить, измерив эти координаты на рисунке сечения, выполненном в большом масштабе[9].
Для определения положения опасных точек построим нейтральную линию, используя формулы (5.12). Радиусы инерции  ,
,  найдены ранее.
найдены ранее.
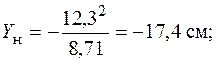
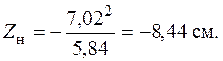
Отложим эти отрезки вдоль главных осей и проведем через полученные точки нейтральную линию  (см. рис. 5.24) . Опасными точками, т. е. точками, наиболее удаленными от нейтральной оси, будут точки 1 и 3 (см. рис. 5.24). В точке 1 действует наибольшее растягивающее напряжение. Запишем условие прочности в этой точке, используя формулу (5.9):
(см. рис. 5.24) . Опасными точками, т. е. точками, наиболее удаленными от нейтральной оси, будут точки 1 и 3 (см. рис. 5.24). В точке 1 действует наибольшее растягивающее напряжение. Запишем условие прочности в этой точке, используя формулу (5.9):
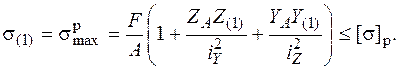
Подставим в условие прочности координаты опасной точки 1 в главных осях, вычислив их по формулам (5.19) или измерив на рисунке, выполненном в масштабе, 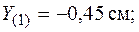
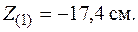 Тогда из условия прочности в точке 1 можно найти допускаемое значение нагрузки:
Тогда из условия прочности в точке 1 можно найти допускаемое значение нагрузки:
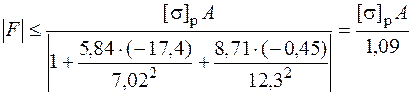 .
.
Для найденного значения допускаемой нагрузки необходимо убедиться, что условие прочности выполняется и в точке 3, которая дальше удалена от нейтральной линии и в которой действует сжимающее напряжение. Для определения напряжения в точке 3 подставим в формулу (5.9) координаты этой точки 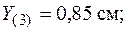
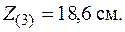
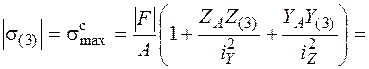
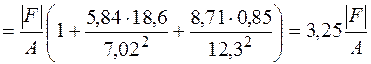
Это напряжение не должно превосходить 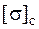 . Если условие прочности в точке с максимальными сжимающими напряжениями выполняться не будет, надо найти значение допускаемой нагрузки заново из условия прочности в этой точке.
. Если условие прочности в точке с максимальными сжимающими напряжениями выполняться не будет, надо найти значение допускаемой нагрузки заново из условия прочности в этой точке.
В заключение построим ядро сечения. Поместим полюсы во внешние угловые точки сечения, т. е. в точки 1, 2, 3, 4, 5 (см. рис. 5.24). Поясним, как получена точка 4, находящаяся на контуре квадранта круга. Отсекая внутреннюю угловую точку 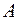 , проводим линию, касательную к контуру сечения (пунктир на рис. 5.24). Точка 4 является точкой касания этой линией квадранта круга. Последовательно находим положение нейтральных линий, соответствующих полюсам в указанных точках, находя отрезки, отсекаемые нейтральными линиями на осях
, проводим линию, касательную к контуру сечения (пунктир на рис. 5.24). Точка 4 является точкой касания этой линией квадранта круга. Последовательно находим положение нейтральных линий, соответствующих полюсам в указанных точках, находя отрезки, отсекаемые нейтральными линиями на осях  ,
,  , по формулам (5.12). Например, если полюс находится в точке 1, то, подставляя в (5.12) координаты точки 1 (
, по формулам (5.12). Например, если полюс находится в точке 1, то, подставляя в (5.12) координаты точки 1 ( 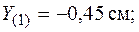
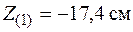 ), найдем
), найдем
 Рис. 5.24. Эпюра напряжений от силы F и ядро сечения Рис. 5.24. Эпюра напряжений от силы F и ядро сечения |
.
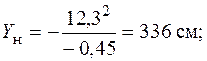
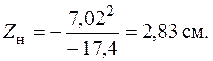
Поскольку 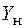 существенно больше
существенно больше 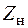 , то это значит, что нейтральная линия 1–1 практически параллельна оси
, то это значит, что нейтральная линия 1–1 практически параллельна оси  . Отрезок
. Отрезок 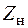 откладываем в масштабе вдоль оси
откладываем в масштабе вдоль оси  и проводим прямую 1–1, параллельную оси
и проводим прямую 1–1, параллельную оси  (см. рис. 5.24). Аналогично строим нейтральные линии, соответствующие полюсам, расположенным в других точках. Ядро сечения (заштрихованная область) показано на рис. 5.24. Отметим, что контур ядра сечения между нейтральными линиями 4–4 и 5–5 очерчен по кривой, так как переход полюса из точки 4 в точку 5 происходит не по прямой линии. На рис. 5.24 показан также эллипс инерции сечения, построенный ранее.
(см. рис. 5.24). Аналогично строим нейтральные линии, соответствующие полюсам, расположенным в других точках. Ядро сечения (заштрихованная область) показано на рис. 5.24. Отметим, что контур ядра сечения между нейтральными линиями 4–4 и 5–5 очерчен по кривой, так как переход полюса из точки 4 в точку 5 происходит не по прямой линии. На рис. 5.24 показан также эллипс инерции сечения, построенный ранее.
