Кожну пряму на площині можна визначити лінійним рівнянням відносно вибраної системи координат; і навпаки, кожне лінійне рівняння визначає пряму в цій координатній системі

Лекція 1.

Тема: Пряма лінія на площині її рівняння та розташування. Економічна інтерпритація.

План лекції

1. Пряма як лінія першого порядку. Загальне рівняння прямої. Дослідження неповного рівняння прямої.

2. Рівняння прямої у відрізках на осях. Параметричні і канонічні рівняння прямої. Рівняння прямої, що проходить через дві задані точки. Рівняння прямої з кутовим коефіцієнтом,

3. Кут між двома прямими. Умови перпендикулярності і паралельності двох прямих.

4. Нормальне рівняння прямої. Відстань від точки до прямої.

1.

З шкільного курсу математики вам відомо, що предметом вивчення геометрії є геометричні об’єкти (точки, лінії, фігури), а предметом вивчення алгебри – числа, рівняння, функції.

Предметом вивчення аналітичної геометрії є вивчення геометричних образів алгебраїчними образами.

Для застосування методів алгебри до розв’язування задач геометрії встановлюється зв’язок між геометричним об’єктом та числами. Способом встановлення такого зв’язку є метод координат, який вперше використав французький математик Рене Декарт (1596-1650).

Основним методом аналітичної геометрії є метод координат.

Таким чином, метод координат дозволяє кожному геометричному образу поставити у відповідність його рівняння, а потім шляхом аналітичного дослідження цього рівняння вивчити властивості цього геометричного об’єкта.

В аналітичній геометрії вивчають дві основні задачі:

1. Складання рівняння геометричного об’єкта, який розглядають як геометричне місце певних точок.

2. Дослідження властивостей геометричного об’єкта за його рівнянням і побудувати його.

Виділяють також дві найпростіші задачі аналітичної геометрії:

1. знаходження відстані між двома точками;

2. ділення відрізка у заданому відношенні.

Кожну пряму на площині можна визначити лінійним рівнянням відносно вибраної системи координат; і навпаки, кожне лінійне рівняння визначає пряму в цій координатній системі.

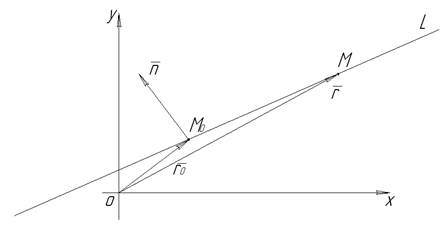
Рис. 1

Означення 1. Рівнянням лініїL у декартовій системі координат на площині називається рівняння виду

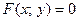
яке задовольняють координати (х, у) у кожній точці цієї лінії і не задовольняють координати жодної іншої точки

Нехай на площині задано пряму L. Складемо ЇЇ рівняння відносно прямокутної системи координат (рис.1). Візьмемо на прямій точку 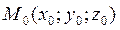, а на площині вектор 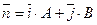, перпендикулярний до L.

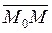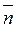Позначимо довільну точку Lчерез М(х, у). Вектори і взаємно перпендикулярні. Отже, скалярний добуток їх дорівнює нулеві: 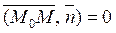. або в координатах:

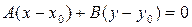(3.1)

Це і є рівняння прямої L. Воно лінійне.

Розглянемо тепер довільне лінійне рівняння:

Ах+Ву+С=0 (3.2)

і нехай 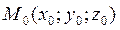є одна з точок, що лежить на цій лінії.

Підставляючи її координати в рівняння (3.2), дістанемо тотожність

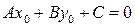
Коли віднімемо цю тотожність, від рівняння (3.2), то отримаємо рівняння:

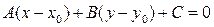
що виражає ту саму лінію, що і рівняння (3.2), і співпадає з рівнянням (3.1). Але це можливо лише тоді, коли лінія (3.2) пряма. Рівняння (3.2)

Ах+Ву+С=0

називають загальним рівнянням прямої на площині.Вектор 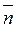,перпендикулярний до прямої L,називають вектором їїнормалі.

Дослідимо, як розміщена пряма відносно системи координат Оху, якщо рівняння (3.2) неповне, тобто коли деякі його коефіцієнти дорівнюють нулю.

Лінію, яка лежить в площині, називається плоскою.

Можливі такі випадки:

1) Якщо коефіцієнт С=0, то пряма проходить через початок координат. Дійсно, в цьому випадку координати точки О(0; 0) задовольняють рівняння (3.2).

2) Якщо В=0, то пряма Ах+С=0паралельна вісі Оу. Справді, вектор її нормалі 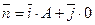перпендикулярний до цієї вісі.

3) Аналогічно, якщо А=0, то пряма паралельна вісі Ох, а вектор її нормалі 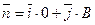перпендикулярний до цієї вісі.

4) Якщо В=С=0, то пряма Ах=0співпадає з віссю Оу. Отже, х= 0 є рівняння вісі Оу.

5) Якщо А = С= 0, то пряма Ву = 0 співпадає з віссю Ох. Отже, у = 0 є рівняння вісі Ох.

Лінії на площині поділяються на алгебраїчні та трансцендентні. Лінія L, яка задана рівнянням 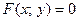називається алгебраїчною, якщо 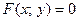є є многочленом від (х; у). Лінії, які не є алгебраїчними, називаються трансцендентними.

Зауваження Іноді замість виразу „задано рівняння лінії” будемо вживати вираз „задана лінія”.