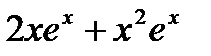A менB жиындарыныңсимметриялықайырымынкөрсететінөрнек:(B\A) (A\B); ;B\ A.
AменBжиындарыныңбірігуінкөрсететінөрнек: 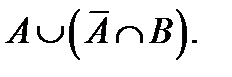 ;
; 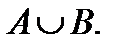 ;
; 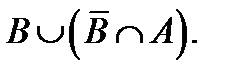
AменBжиындарыныңқиылысуынкөрсететінөрнек: 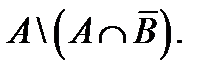 ;
; 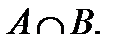 ;
; 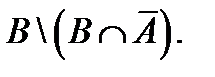
f (x) = x3 +4 x – 5 функциясының туындысы : y = 3x2 +4; y – 4 =3
f (x)= x2 +x-2 функциясы үшін айтылған пікір орыныды 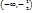 - кему аралығы;
- кему аралығы; 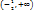 - өсу аралығы
- өсу аралығы
F(X) функциясының (1, 2) аралығындағы үлестіріуін табыңыз: В) 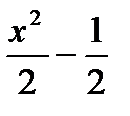 ;
;
f(x)= 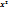 -10x-6 функциясы үшін мына тұжырым дұрыс: (-
-10x-6 функциясы үшін мына тұжырым дұрыс: (- 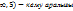 ;(5,+
;(5,+ 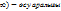 ; x=5, минимум нүктес
; x=5, минимум нүктес
u = 2xy 3 -9 функциясының  дербез туындысының м 0 ( 1 :1) нүктесіндегі мәні мына аралықта жатады : (-10,10); ( -8,8 ); ( -
дербез туындысының м 0 ( 1 :1) нүктесіндегі мәні мына аралықта жатады : (-10,10); ( -8,8 ); ( - 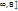
U жиыныныѕ ішкі жиындары A мен B –ныѕ айырымын көрсететін өрнек: 1 A\ (A  U) 2)
U) 2) 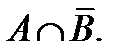 3)
3) 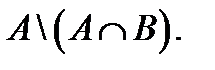
U жиынының ішкі жиындары A мен B –ның бірігуін көрсететін өрнек: 1 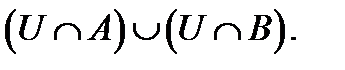 2)
2) 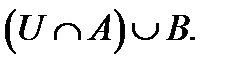 3)
3) 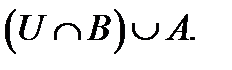
UжиыныныңішкіжиындарыAменB–ныңбірігуінкөрсететінөрнек: 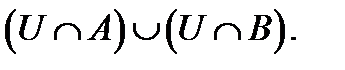 ;
; 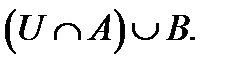 ;
; 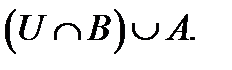
x*y’’=y’теңдеуінің шешімі: y=2x2+2
x=0, y=0, x+y=1 сызықтарымен қоршалған жазық фигураның ауданына тең сан мына теңсіздіктердің қанағаттандырады: 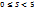 ;
; 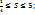
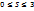
y (x)= x . ctgx функциясының туыныдысы :y = 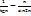
y'' = 4y теңдеуінің шешімі: 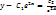 ;
; 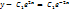 ;
; 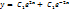
y = x 3,x = 1, y=0 сызыктарымен коршалған жазық фигураның ауданына тен сан мына аралықта жатады 0 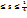 ; 0
; 0 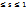
y … - y = 0 теңдеуінің шешімі :y = C1 +C2x+C 3 ex
y’= 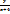 , y(0)=8 Коши есебінің шешімі:y=eln2x+4; ln y=ln2+ln
, y(0)=8 Коши есебінің шешімі:y=eln2x+4; ln y=ln2+ln 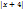
y= 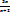 функциясы үшін x=-2 нүктесі: Үзіліс нүктесі; ІІ текті үзіліс нүктесі; нүктеде функция анықталмайды
функциясы үшін x=-2 нүктесі: Үзіліс нүктесі; ІІ текті үзіліс нүктесі; нүктеде функция анықталмайды
y-2x=0, y(0)=3 Коши есебініің шешімі :y=3+x2
z = x2 y +xsin y функциясы үшін дұрыс катынастар 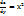 +x cos y;
+x cos y;  =2 xy +sin y;
=2 xy +sin y; 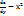 = xcos y
= xcos y
z = x3 + y 3 функциясының толық дифференциалы: 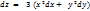 ;
; 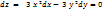 ;
; 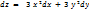
А (-4;5) , В(3;5) нүктелері берілген. Екі нүкте арқылы өтетін түзу теңдеуін жаз. Д) у=5
А(2,3) және В(-1,2) нүктелері берілген. 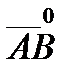 бірлік векторының координаталарын көрсетіңіз: В)
бірлік векторының координаталарын көрсетіңіз: В) 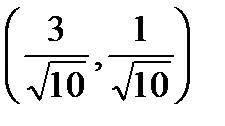
А(2;1) нүктесі арқылы х+2у+1=0 түзуіне параллель өтетін түзу теңдеуін жазыңыз:х+2у-4=0
А(2;1;1) нүктесінен 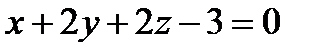 жазықтығына дейінгі арақашықтық: Е) 1
жазықтығына дейінгі арақашықтық: Е) 1
А(-3;0) В(3;6) нүктелері берілген. Шеңбердің радиусын тап. В) 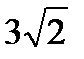
А(-4;5) , В(3;5) нүктелері берілген. Екі нүкте арқылы өтетін түзу теңдеуін жаз.Е) у=5
А(-5;5;3) нүктесінен 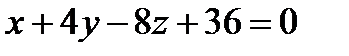 жазықтығына дейінгі арақашықтық тең: Е) 3
жазықтығына дейінгі арақашықтық тең: Е) 3
А(-6;-1) , В(10;4) және С(-2;1) төбелерімен берілген үшбұрыштың ауданы тең болады: 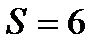
Анықталған интегралдың бөліктеп интегралдау формуласы мынадай:С) 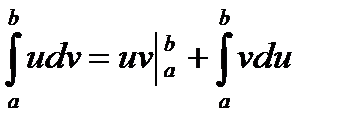
Анықталмаған 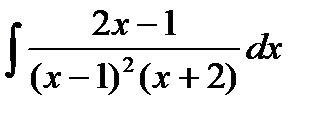 интегралын есептеу үшін көрсетілген тәсілдердің қайсысы қолданылады: Д) Интеграл астындағы функцияны жай бөлшектерге жіктеу
интегралын есептеу үшін көрсетілген тәсілдердің қайсысы қолданылады: Д) Интеграл астындағы функцияны жай бөлшектерге жіктеу
Анықталмаған интервал үшін дұрыс формулалар: 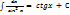 ;
; 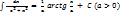 ;
; 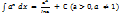
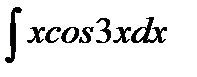 анықтамаған интеграл тең:С)
анықтамаған интеграл тең:С) 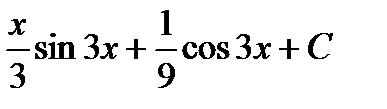
Анықтауышты есептеңіз: 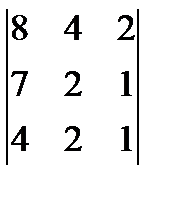 С) 0
С) 0
Анықтауышты есептеңіз 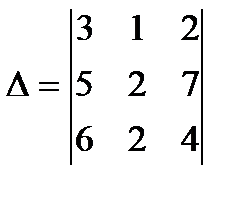 В) 0
В) 0
Анықтауышты есептеңіз 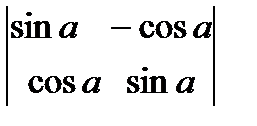 Д) 1
Д) 1
Анықтауыштың 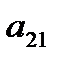 элементінің миноры
элементінің миноры 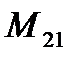 есептеңіз
есептеңіз 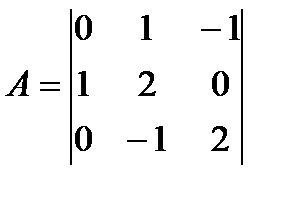 : В) 1;
: В) 1;
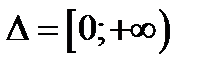 аралығында берілген
аралығында берілген 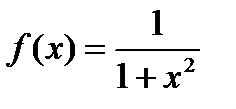 функциясының алғашқы
функциясының алғашқы 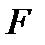 функциясы1)
функциясы1) 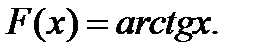 2)
2) 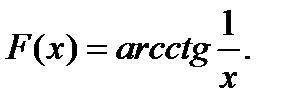 3)
3) 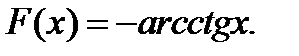
Атқыштың нысанаға тигізу ықтималдығы 0,7 болса, онда 2 рет атқанда кем дегенде бір рет тигізу ықтималдығын табыңыз: С) 0,91
берілген функциялардың туындылары үшін дұрыс формулалар: ( 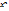 )`=
)`= 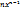
Берілген функциялардың туындылары үшін дұрыс формулалар: ( 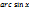 )’= -
)’= - 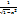 ; (arc
; (arc 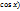 ’=-
’=- 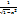
Берілген функциялардың туындылары үшін дұрыс формулалар: 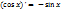 ;
; 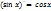
Берілгендердің арасындағы дифференциалдық теңдеу болатыны:1) 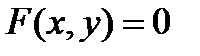 2)
2) 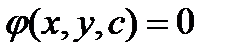 3)
3) 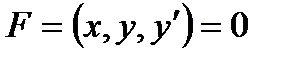 4)
4) 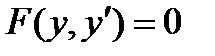 5)
5) 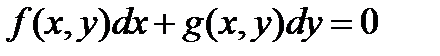 Е) 3,4,5
Е) 3,4,5
Босжиындыкөрсететінөрнек: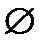 ;
; 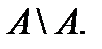 ;
; 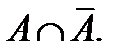
Бөліктеп интегралдау формуласын көрсетіңіз: А) 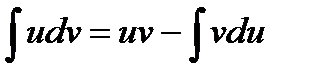
Бұрыштық коэффициенті 3 және А) (-2;3) нүктесі арқылы өтетін түзудің теңдеуіС 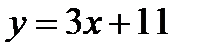
Бірінші ретті сызықтық дифференциалдық теңдеуді көрсетіңіз:Е) 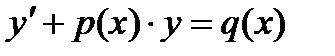
Бірінші ретті 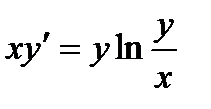 дифференциалдық теңдеуінің түрін анықтаңыз:Е) Айнымалыларға байланысты біртекті дифференциалдық теңдеу.
дифференциалдық теңдеуінің түрін анықтаңыз:Е) Айнымалыларға байланысты біртекті дифференциалдық теңдеу.
Бірінші ретті сызықтық теңдеу 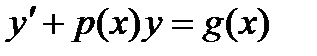 келесі ауыстыру арқылы шешіледі.С)
келесі ауыстыру арқылы шешіледі.С) 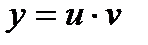
Бірінші ретті дифференциалдық теңдеудің жалпы шешімінің түрі:Е) 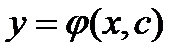
В(5,10) нүктесі арқылы өтетін және 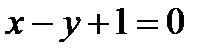 түзуіне перпендикуляр түзудің теңдеуіА)
түзуіне перпендикуляр түзудің теңдеуіА) 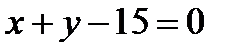
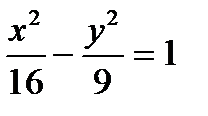 гиперболаның фокусын табыңыз.Е) с=5
гиперболаның фокусын табыңыз.Е) с=5
Дәрежелік қатардың 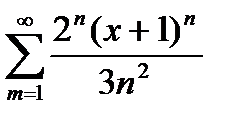 жалпы мүшесінің коэффициенті тең: Е)
жалпы мүшесінің коэффициенті тең: Е) 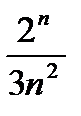
Дәрежелік қатардың 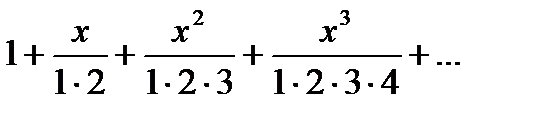 жалпы мүшесі келесі функция болады:Д)
жалпы мүшесі келесі функция болады:Д) 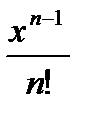
Дәрежелік қатардың 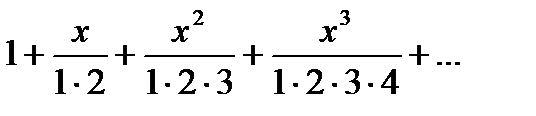 жалпы мүшесі келесі функция болады.В)
жалпы мүшесі келесі функция болады.В) 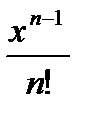
Дәрежелік қатардың 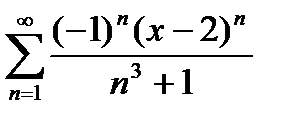 жалпы мүшесі келесі өрнек болады: С)
жалпы мүшесі келесі өрнек болады: С) 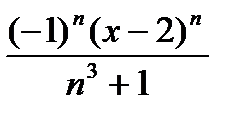
Дәрежелік қатардың 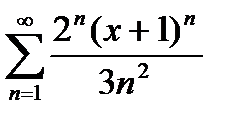 жалпы мүшесін келесі өрнек болады: Д)
жалпы мүшесін келесі өрнек болады: Д) 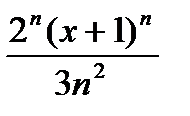
Дәрежелік қатардың 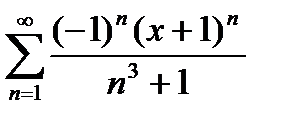 жалпы мүшесінің коэффициенті тең:. В)
жалпы мүшесінің коэффициенті тең:. В) 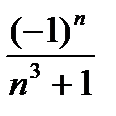
Дәрежелік қатардың 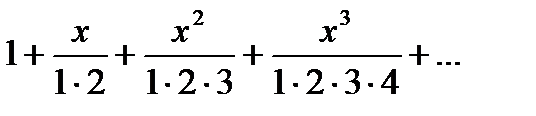 жалпы мүшесі келесі функция болады.В)
жалпы мүшесі келесі функция болады.В) 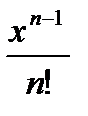
Дәрежелік қатардың 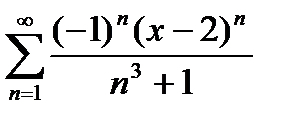 жалпы мүшесі келесі өрнек болады;Д)
жалпы мүшесі келесі өрнек болады;Д) 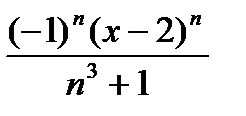 Е)х-2
Е)х-2
Дәрежелік қатардың 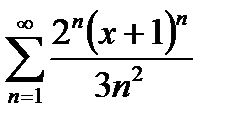 жалпы мүшесі келесі өрнек болады: А)
жалпы мүшесі келесі өрнек болады: А) 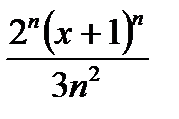
Дәрежелік қатардың 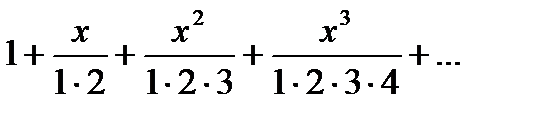 жалпы мүшесі келесі функция болады:
жалпы мүшесі келесі функция болады: 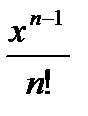
Дәрежелік қатардың 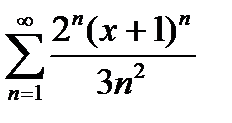 жалпы мүшесінің коэффициенті тең: С)
жалпы мүшесінің коэффициенті тең: С) 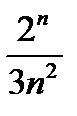
Дәрежелік қатардың 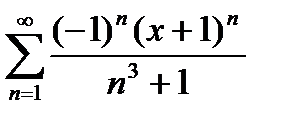 жалпы мүшесінің коэффициенті тең:Д)
жалпы мүшесінің коэффициенті тең:Д) 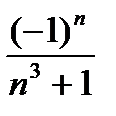
Дәрежелік қатардың 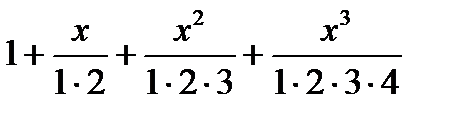 +... жалпы мүшесі келесі функция болады: Д)
+... жалпы мүшесі келесі функция болады: Д) 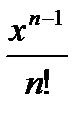
Дәрежелік қатардың 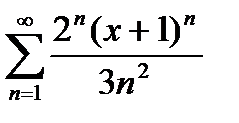 жалпы мүшесі келесі өрнек болады: А)
жалпы мүшесі келесі өрнек болады: А) 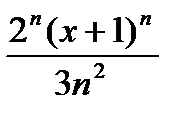
Дискретті кездейсоқ шама Х үлестіру заңы арқылы берілген. 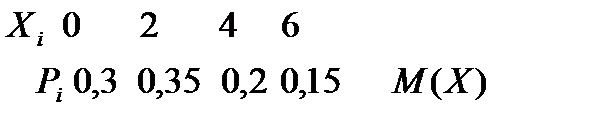 табыңыз: С) 2,4
табыңыз: С) 2,4
Дискретті кездейсоқ шама Х-тің дисперсиясын табыңыз: 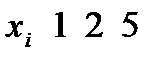 ,
, 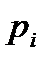 0,6 0,2 0,2 С) 2,4
0,6 0,2 0,2 С) 2,4
Дифференциялдың дұрыс дережелері: 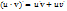 ;
; 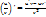
Дұрыс формуланы көрсетіңіз: 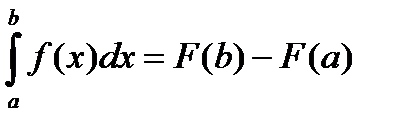
Егер 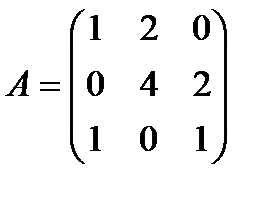 берілсе, онда А2 матрицасы В)
берілсе, онда А2 матрицасы В) 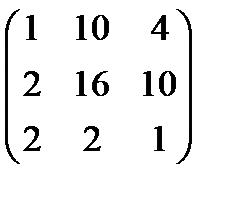
Егер 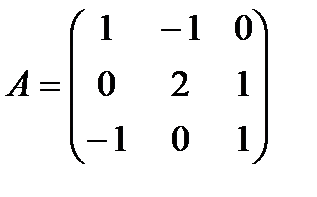 матрицасының кері матрицасы болса, онда оны табыңыз:Е)
матрицасының кері матрицасы болса, онда оны табыңыз:Е) 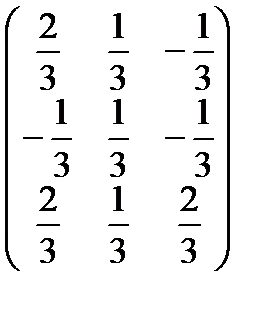
Егер 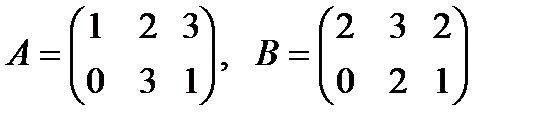 берілсе ,
берілсе , 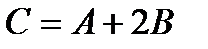 матрицасын табыңыз.Д)
матрицасын табыңыз.Д) 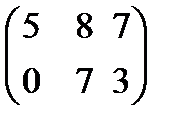
Егер 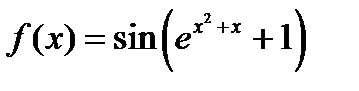 берілсе, онда:
берілсе, онда: 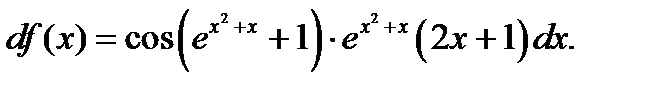
Егер 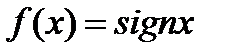 берілсе, онда:
берілсе, онда: 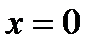 - функцияның 1текті үзіліс нүктесі
- функцияның 1текті үзіліс нүктесі 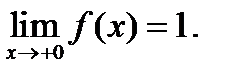 ;
; 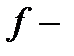 тақ функция
тақ функция
Егер 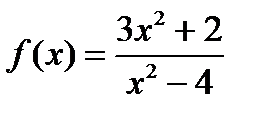 берілсе, онда:
берілсе, онда: 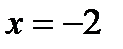 - функцияның 2 - текті үзіліс нүктесі
- функцияның 2 - текті үзіліс нүктесі
Егер 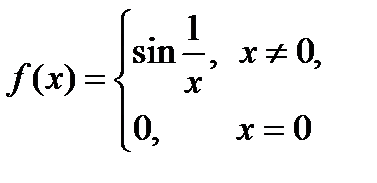 берілсе, онда:
берілсе, онда: 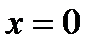 - функцияның 2-текті үзіліс нүктесі
- функцияның 2-текті үзіліс нүктесі 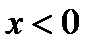 нүктелерінде функция үзіліссіз;
нүктелерінде функция үзіліссіз; 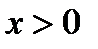 нүктелерінде функция үзіліссіз
нүктелерінде функция үзіліссіз
Егер 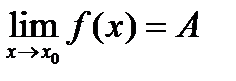 берілсе, онда:
берілсе, онда: 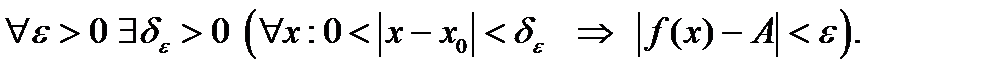 ;
; 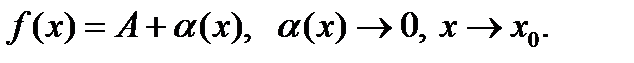 ;
; 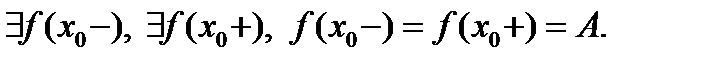
Егер 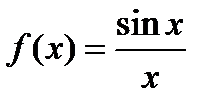 берілсе, онда:
берілсе, онда: 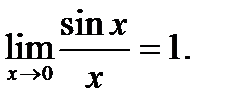 ;
; 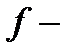 жұп функция.;
жұп функция.; 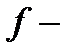 функциясы
функциясы 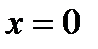 нүктесінің маңайында шенелген
нүктесінің маңайында шенелген
Егер 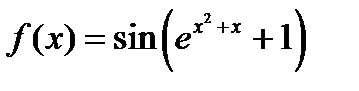 берілсе, онда:1
берілсе, онда:1 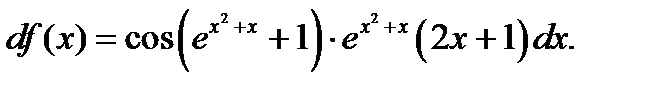
Егер 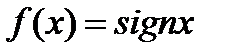 берілсе, онда: 1
берілсе, онда: 1 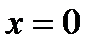 - функцияның 1текті үзіліс нүктесі 2)
- функцияның 1текті үзіліс нүктесі 2) 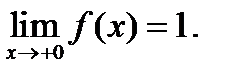
Егер 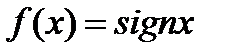 берілсе, онда: 1
берілсе, онда: 1 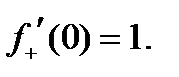 2)
2) 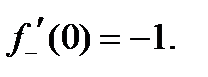 3)
3) 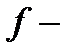 тақ функция
тақ функция
Егер 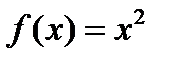 берілсе, онда:1
берілсе, онда:1 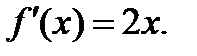 2) оның
2) оның 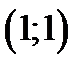 нүктедегі жанамасы
нүктедегі жанамасы 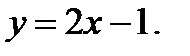
Егер 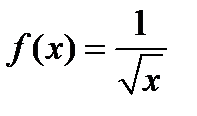 берілсе, онда:1
берілсе, онда:1 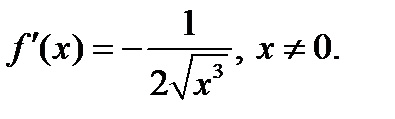 2) оның
2) оның 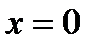 нүктесінде туындысы жоқ
нүктесінде туындысы жоқ
Егер 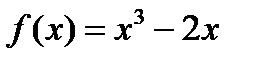 берілсе, онда: 1
берілсе, онда: 1 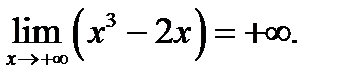 2)
2) 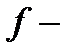 тақ функция 3)
тақ функция 3) 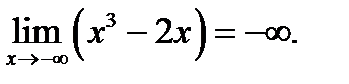
Егер 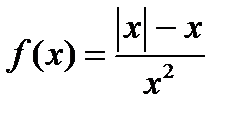 берілсе, онда: 1
берілсе, онда: 1 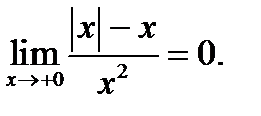 2)
2) 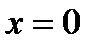 -үзіліс нүктесі 3)
-үзіліс нүктесі 3) 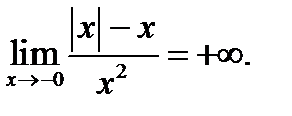
Егер 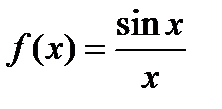 берілсе, онда: 1)
берілсе, онда: 1) 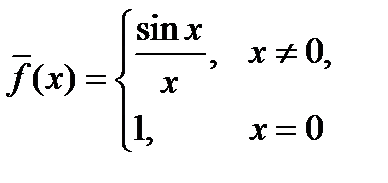 - үзіліссіз функция 2)
- үзіліссіз функция 2) 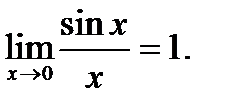
Егер 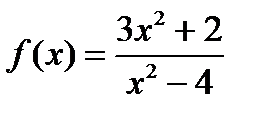 берілсе, онда:1)
берілсе, онда:1) 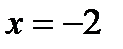 - функцияның 2 - текті үзіліс нүктесі
- функцияның 2 - текті үзіліс нүктесі
Егер 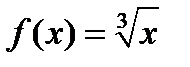 берілсе, онда: 1)
берілсе, онда: 1) 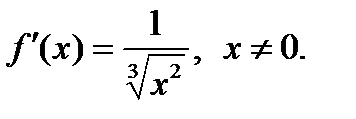 2)
2) 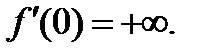 3) ол
3) ол 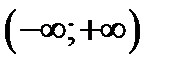 аралығында үзіліссіз функция.
аралығында үзіліссіз функция.
Егер 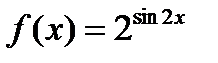 берілсе, онда: 1)
берілсе, онда: 1) 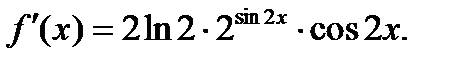 2) ол
2) ол 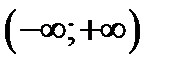 аралығында үзіліссіз
аралығында үзіліссіз
Егер 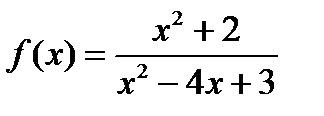 берілсе, онда:1)
берілсе, онда:1) 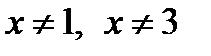 нүктелерде функция үзіліссіз 2)
нүктелерде функция үзіліссіз 2) 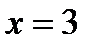 - функцияның 2 - текті үзіліс нүктесі 3)
- функцияның 2 - текті үзіліс нүктесі 3) 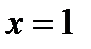 - функцияның 2 - текті үзіліс нүктесі
- функцияның 2 - текті үзіліс нүктесі
Егер 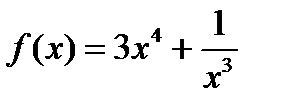 берілсе, онда: 1)
берілсе, онда: 1) 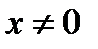 нүктелерінде функция үзіліссіз 2)
нүктелерінде функция үзіліссіз 2) 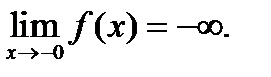
Егер 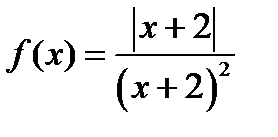 берілсе, онда:1)
берілсе, онда:1) 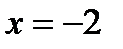 нүктеде функция анықталмаған 2)
нүктеде функция анықталмаған 2) 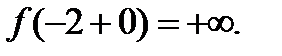 3)
3) 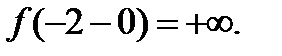
Егер 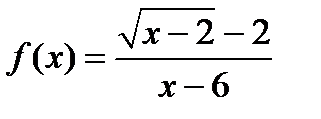 берілсе, онда: 1)
берілсе, онда: 1) 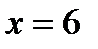 нүктесінде
нүктесінде 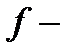 анықталмаған 2)
анықталмаған 2) 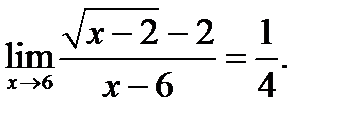
Егер 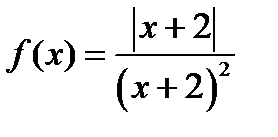 берілсе, онда:
берілсе, онда: 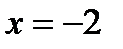 нүктеде функция анықталмаған
нүктеде функция анықталмаған 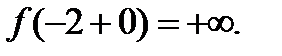 ;
; 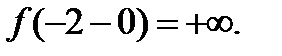
Егер 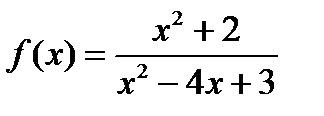 берілсе, онда:
берілсе, онда: 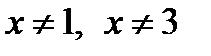 нүктелерде функция үзіліссіз;
нүктелерде функция үзіліссіз; 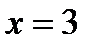 - функцияның 2 - текті үзіліс нүктесі;
- функцияның 2 - текті үзіліс нүктесі; 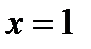 - функцияның 2 - текті үзіліс нүктесі
- функцияның 2 - текті үзіліс нүктесі
Егер 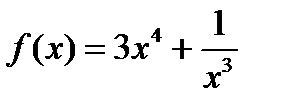 берілсе, онда:
берілсе, онда: 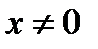 нүктелерінде функция үзіліссіз
нүктелерінде функция үзіліссіз 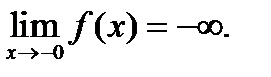 ;
; 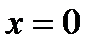 - функцияның 2 - текті үзіліс нүктесі
- функцияның 2 - текті үзіліс нүктесі
Егер 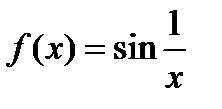 берілсе, онда:
берілсе, онда: 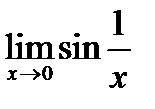 шегі жоқ;
шегі жоқ; 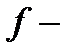 тақ функция;
тақ функция; 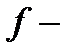 шенелген функция
шенелген функция
Егер 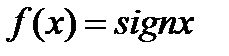 берілсе, онда:: 1)
берілсе, онда:: 1) 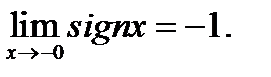 2)
2) 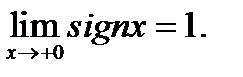 3)
3) 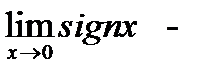 шегі жоқ
шегі жоқ
Егер 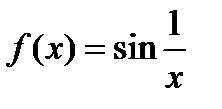 берілсе, онда:: 1)
берілсе, онда:: 1) 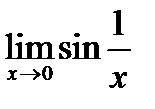 шегі жоқ 2)
шегі жоқ 2) 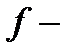 тақ функция 3)
тақ функция 3) 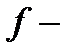 шенелген функция
шенелген функция
Егер 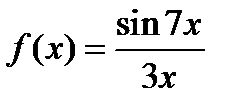 берілсе, онда:: 1)
берілсе, онда:: 1) 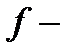 жўп функция 2)
жўп функция 2) 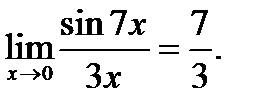 3) функция
3) функция 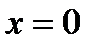 нүктеде анықталмаған
нүктеде анықталмаған
Егер 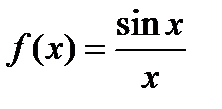 берілсе, онда:;
берілсе, онда:; 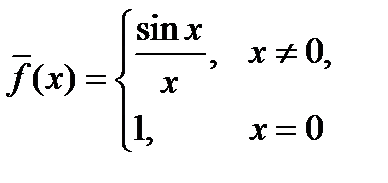 - үзіліссіз функция
- үзіліссіз функция 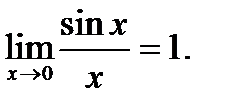 ;
; 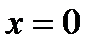 - функцияның жойылатын үзіліс нүктесі
- функцияның жойылатын үзіліс нүктесі
Егер 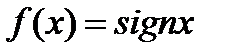 берілсе, онда:
берілсе, онда: 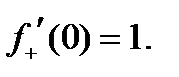 ;
; 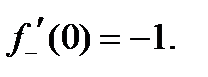 ;
; 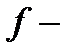 таќ функция
таќ функция
Егер 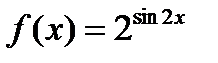 берілсе, онда:
берілсе, онда: 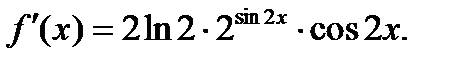 ; ол
; ол 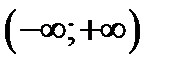 аралыєында їзіліссіз;
аралыєында їзіліссіз; 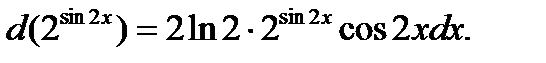
Егер 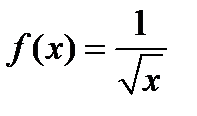 берілсе, онда:
берілсе, онда: 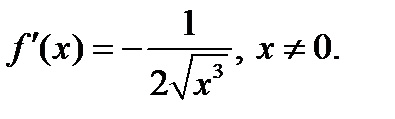 ; оныѕ
; оныѕ 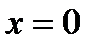 нїктесінде туындысы жоќ;
нїктесінде туындысы жоќ; 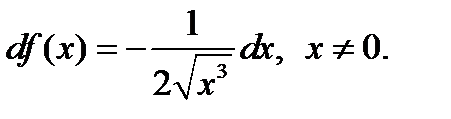
Егер 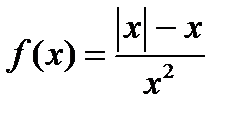 берілсе, онда:
берілсе, онда: 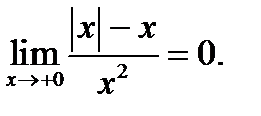 ;
; 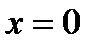 -үзіліс нүктесі;
-үзіліс нүктесі; 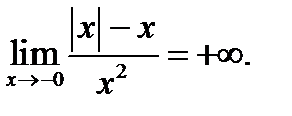
Егер 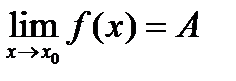 берілсе, онда:1)
берілсе, онда:1) 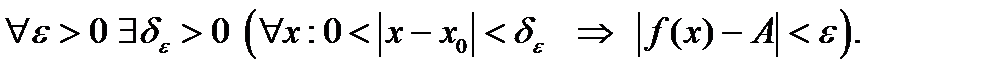
Егер 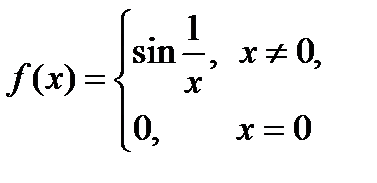 берілсе, онда:1)
берілсе, онда:1) 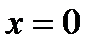 - функцияның 2-текті үзіліс нүктесі
- функцияның 2-текті үзіліс нүктесі
Егер 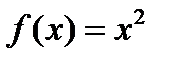 берілсе, онда:B)
берілсе, онда:B) 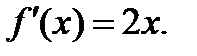 ;оныѕ
;оныѕ 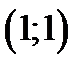 нїктедегі жанамасы
нїктедегі жанамасы 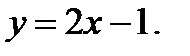 ;оныѕ
;оныѕ 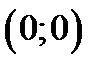 нїктедегі жанамасыныѕ бўрыштыќ коэффициенті
нїктедегі жанамасыныѕ бўрыштыќ коэффициенті 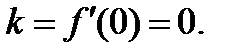
Егер 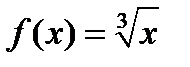 берілсе, онда:C)
берілсе, онда:C) 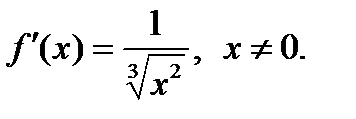 ;
; 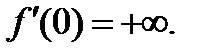 ; ол
; ол 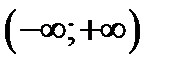 аралыєында їзіліссіз функция.
аралыєында їзіліссіз функция.
Егер 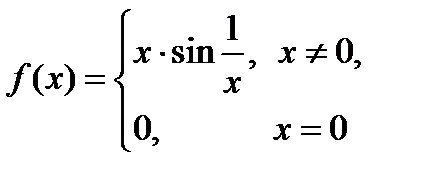 берілсе, онда:
берілсе, онда: 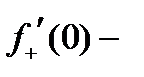 жоќ;
жоќ; 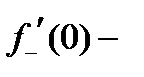 жоќ;ол
жоќ;ол 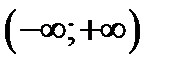 аралыєында їзіліссіз
аралыєында їзіліссіз
Егер 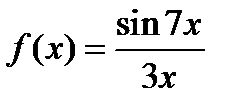 берілсе, онда:
берілсе, онда: 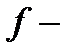 жұп функция;
жұп функция; 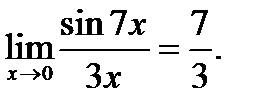 ;функция
;функция 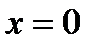 нүктеде анықталмаған
нүктеде анықталмаған
Егер 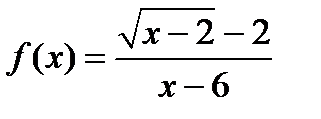 берілсе, онда:
берілсе, онда: 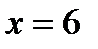 нүктесінде
нүктесінде 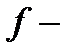 анықталмаған
анықталмаған 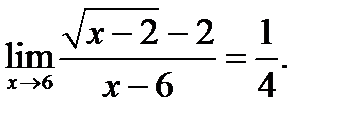 ;Анықталу аймағы
;Анықталу аймағы 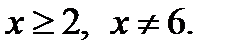
Егер 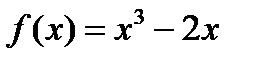 берілсе, онда:
берілсе, онда: 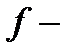 функциясы периодты.;
функциясы периодты.; 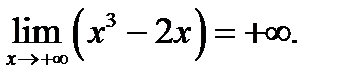
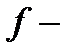 тақ функция;
тақ функция; 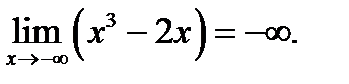
Егер 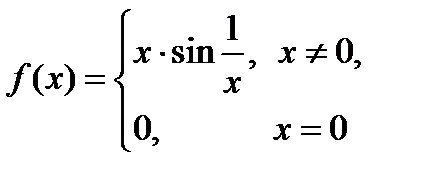 берілсе,онда:1)
берілсе,онда:1) 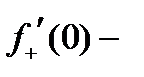 жоқ 2) E)
жоқ 2) E) 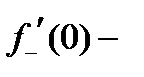 жоқ 3) ол
жоқ 3) ол 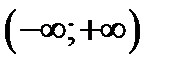 аралығында үзіліссіз
аралығында үзіліссіз
Егер 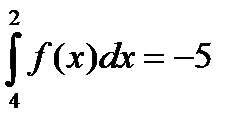 болса, онда
болса, онда 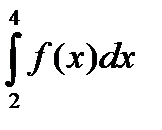 С) 5
С) 5
Егер 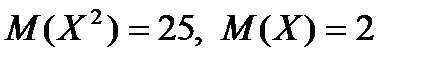 болса, онда дискретті кездейсоқ шама Х-тің дисперсиясын Д(Х)-ті табыңыз: В) 21
болса, онда дискретті кездейсоқ шама Х-тің дисперсиясын Д(Х)-ті табыңыз: В) 21
Егер 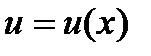 болса, онда
болса, онда 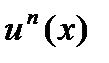 функциясының туындысыА)
функциясының туындысыА) 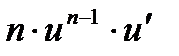
Егер 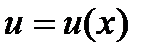 болса, онда
болса, онда 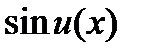 функциясының туындысыС)
функциясының туындысыС) 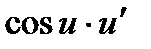
Егер 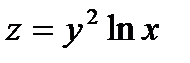 болса, онда
болса, онда 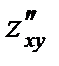 тең: Е)
тең: Е) 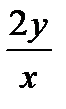
Егер 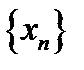 сандық тізбектің шегі а тең болса, онда: 1)
сандық тізбектің шегі а тең болса, онда: 1) 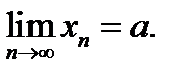 2)
2) 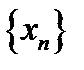 -шенелген тізбек
-шенелген тізбек
Егер 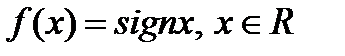 функциясы берілсе, онда: 1) оның алғашқы функциясы бар
функциясы берілсе, онда: 1) оның алғашқы функциясы бар
Егер 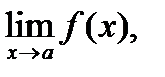
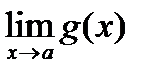 шектері бар және олар ақырлы болса, онда:
шектері бар және олар ақырлы болса, онда: 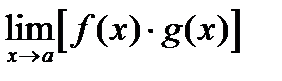 шегі де бар;
шегі де бар; 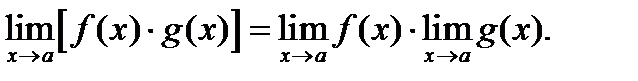
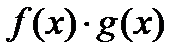 функциясы
функциясы 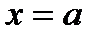 нүктесінің маңайында шенелген
нүктесінің маңайында шенелген
Егер  сандық тізбектің шегі а тең болса, онда:
сандық тізбектің шегі а тең болса, онда: 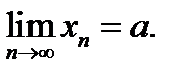 ;
; 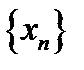 -шенелген тізбек;
-шенелген тізбек; 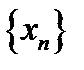 - ақырсыз аз шама
- ақырсыз аз шама
Егер f функциясы 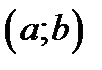 аралығында кемімелі болса, онда:
аралығында кемімелі болса, онда: 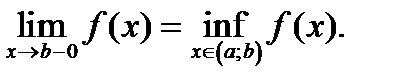
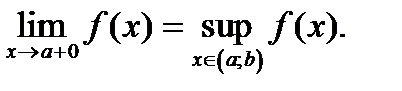 ;f төменнен шенелмеген жағдайда
;f төменнен шенелмеген жағдайда 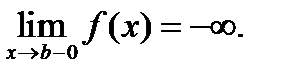
Егер ƒ(x), g(x), h(x) - функциялары 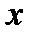 нїктесінде дифференциалданса, онда:
нїктесінде дифференциалданса, онда: 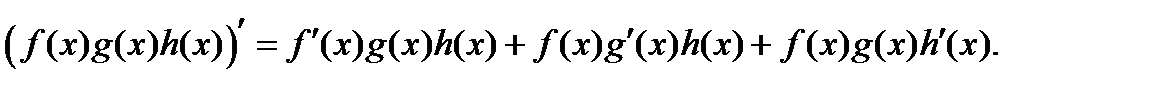 ;
; 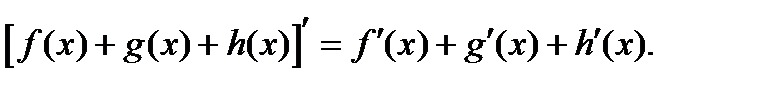 ;
; 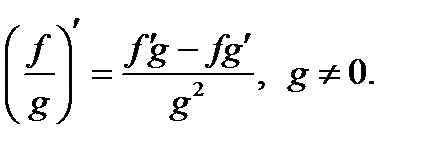
Егер M саны 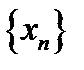 сандық тізбектің жоғарғы шегі болса, онда:
сандық тізбектің жоғарғы шегі болса, онда: 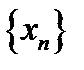 тізбегі үшін Коши шарты орындалады;
тізбегі үшін Коши шарты орындалады; 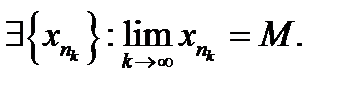 ;
; 


Егер z=2x2-xy болса ,онда М (-1,2) нүктесіндегі z’x+z’y мәні мына аралықта жатады: (-5,-1); (-8,8); (-10,-2)
Егер z=5 xy-y2 болса онда М(1,-2) нүктесіндегі z’x+z’y мәні мына аралықта жатады: (-3,3)
Егер А(1;2;-3), В(2;4;-5) нүктелері берілсе, онда 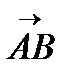 векторының ұзындығыД) 3
векторының ұзындығыД) 3
Егер 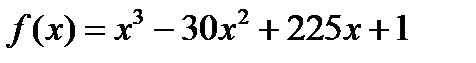 берілсе, онда:1)
берілсе, онда:1) 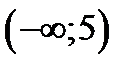 аралығында фунция өседі
аралығында фунция өседі
Егер 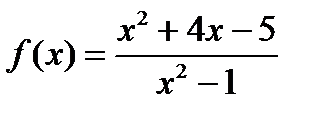 берілсе, онда:
берілсе, онда: 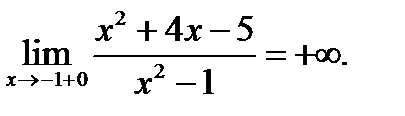 ;
; 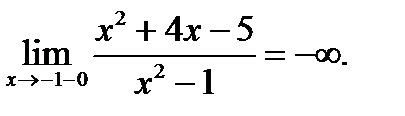
Егер 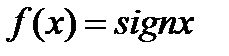 берілсе, онда:
берілсе, онда: 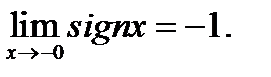 ;
; 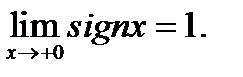 ;
; 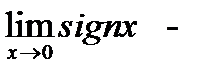 шегі жоқ
шегі жоқ
Егер 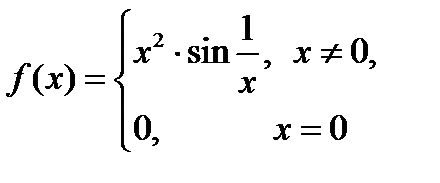 берілсе, онда:1) оның
берілсе, онда:1) оның 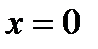 нүктесіндегі жанамасы:
нүктесіндегі жанамасы: 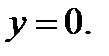
Егер 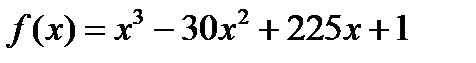 берілсе, онда:
берілсе, онда: 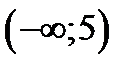 аралыєында фунция ґседі; вертикаль асимптота жоќ; (1;+
аралыєында фунция ґседі; вертикаль асимптота жоќ; (1;+ 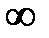 )аралыєында функция ойыс (график дґѕестігі тґмен ќараєан)
)аралыєында функция ойыс (график дґѕестігі тґмен ќараєан)
Егер В жиыны А жиынының ішкі жиыны болса, онда 1)  2)
2) 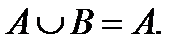
Егер 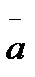 және
және 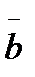 векторлары
векторлары 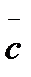 векторына перпендикуляр болса, онда мына теңдік
векторына перпендикуляр болса, онда мына теңдік 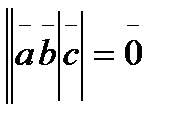 орындала ма? В) иә
орындала ма? В) иә
Егер қандай бір аралықта 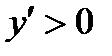 , онда функция
, онда функция 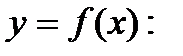 Е) өседі
Е) өседі
Егер мынадай ақырлы шектер бар болса, онда 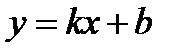 функция көлбеу асимптотаны анықтайды. В)
функция көлбеу асимптотаны анықтайды. В) 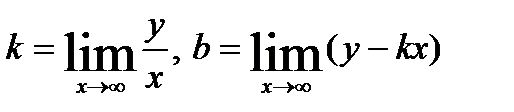
Егер мынадай ақырлы шектер бар болса, онда 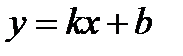 функция көлбеу асимптотаны анықтайды.С)
функция көлбеу асимптотаны анықтайды.С) 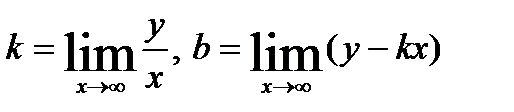
Егер 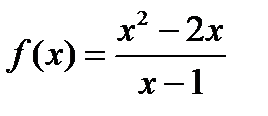 функциясы берілсе, онда: 1) оның вертикаль асимптотасы
функциясы берілсе, онда: 1) оның вертикаль асимптотасы 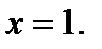
Егер 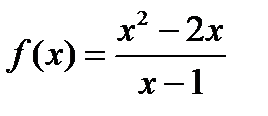 функциясы берілсе, онда: оныѕ вертикаль асимптотасы
функциясы берілсе, онда: оныѕ вертикаль асимптотасы 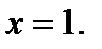 ;оныѕ кґлбеу асимптотасы
;оныѕ кґлбеу асимптотасы 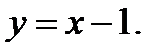 ;
;  аралыєында ол ґседі
аралыєында ол ґседі
Егер 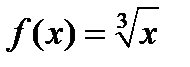 функциясы берілсе, онда:1) ол
функциясы берілсе, онда:1) ол 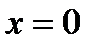 нүктесінде өседі
нүктесінде өседі
Егер 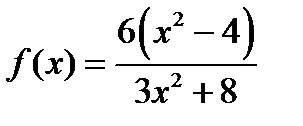 функциясы берілсе, онда:асимптотасы y=2, тїзуі;
функциясы берілсе, онда:асимптотасы y=2, тїзуі; 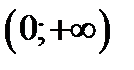 аралыєында ґседі; оныѕ еѕ кіші мјні
аралыєында ґседі; оныѕ еѕ кіші мјні 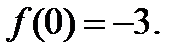
Егер 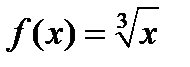 функциясы берілсе, онда:ол
функциясы берілсе, онда:ол 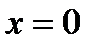 нїктесінде ґседі;
нїктесінде ґседі; 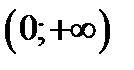 аралыєында ол дґѕес (график дґѕестігі жоєары баєытталєан);
аралыєында ол дґѕес (график дґѕестігі жоєары баєытталєан); 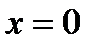 - оныѕ иілу нїктесі
- оныѕ иілу нїктесі
Егер 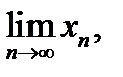
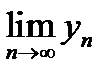 шектері бар болса, онда:1)
шектері бар болса, онда:1) 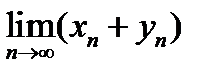 шегі бар 2)
шегі бар 2) 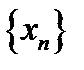 -шенелген тізбек 3)
-шенелген тізбек 3) 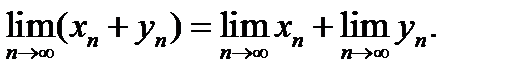
Егер 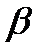 -саныЕжиыныныңдәлжоғарғышекарасыболса, онда:
-саныЕжиыныныңдәлжоғарғышекарасыболса, онда: 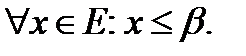 ;
; 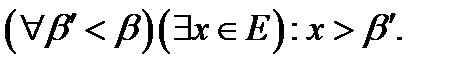 ;
; 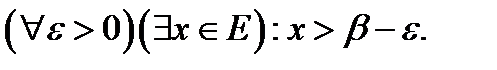
Егер 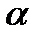 саныЕжиыныныңдәлтөменгішекарасыболса, онда:
саныЕжиыныныңдәлтөменгішекарасыболса, онда: 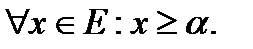 ;
; 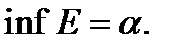
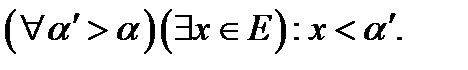
ЕгерВжиыныАжиыныныңішкіжиыныболса, онда  ;
; 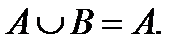 ;
; 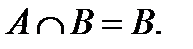
Егер 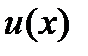 және
және 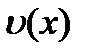 функцияларының
функцияларының 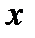 нүктеде туындылары бар болса, онда:
нүктеде туындылары бар болса, онда:
Егер 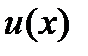 және
және 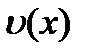 функцияларының
функцияларының 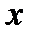 нүктеде туындылары бар болса, онда:1)
нүктеде туындылары бар болса, онда:1) 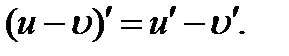 2)
2) 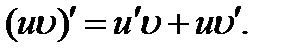 3)
3) 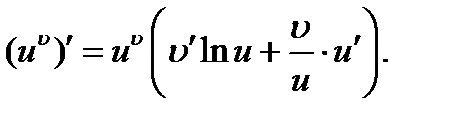
Егер 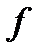 және g функциялары
және g функциялары 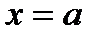 нүктеде үзіліссіз болса, онда:
нүктеде үзіліссіз болса, онда: 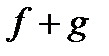 функциясы
функциясы 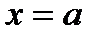 нүктеде үзіліссіз;
нүктеде үзіліссіз; 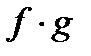 функциясы
функциясы 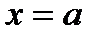 нүктеде үзіліссіз;
нүктеде үзіліссіз; 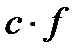 (с – тұрақты) функциясы
(с – тұрақты) функциясы 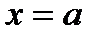 нүктеде үзіліссіз
нүктеде үзіліссіз
Егер 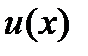 жјне
жјне 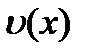 функцияларыныѕ
функцияларыныѕ 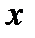 нїктеде туындылары бар болса, онда: (u+х)ґ=uґ+хґ;
нїктеде туындылары бар болса, онда: (u+х)ґ=uґ+хґ; 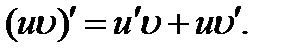 ;
; 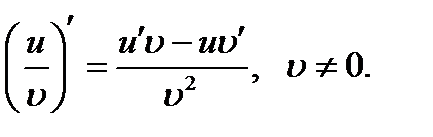
Егер 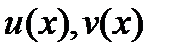 функцияларыныѕ
функцияларыныѕ 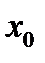 нїктесінде n ретке дейінгі туындылары бар болса, онда:
нїктесінде n ретке дейінгі туындылары бар болса, онда: 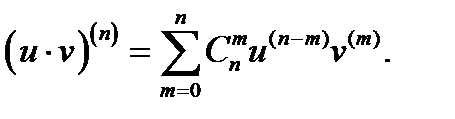 ;
; 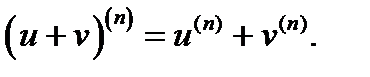 ;
; 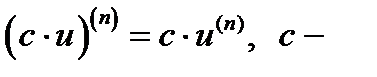 тўраќты
тўраќты
Егер 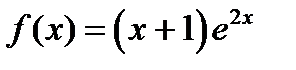 функциясы берілсе, онда: 1 ол
функциясы берілсе, онда: 1 ол 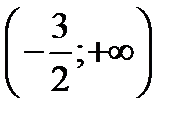 аралығында өседі 2) (-2;+
аралығында өседі 2) (-2;+ 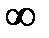 ) аралығында функция ойыс (дөңестігі төмен бағытталған)3) функцияның асимптотасы жоқ
) аралығында функция ойыс (дөңестігі төмен бағытталған)3) функцияның асимптотасы жоқ
Егер 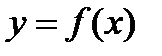 функциясы қандай да бір
функциясы қандай да бір 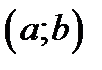 аралығында, ал
аралығында, ал 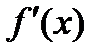 қандай да бір
қандай да бір 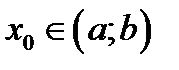 нүктесінде дифференциалданса, онда:1
нүктесінде дифференциалданса, онда:1 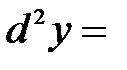 ƒ"
ƒ" 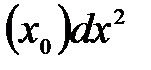 2) функция
2) функция 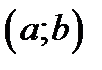 аралығында үзіліссіз 3)
аралығында үзіліссіз 3) 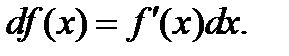
Егер 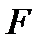 функциясы
функциясы 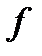 функциясыныѕ
функциясыныѕ  аралыєындаєы алєашќы функциясы болса,онда:
аралыєындаєы алєашќы функциясы болса,онда: 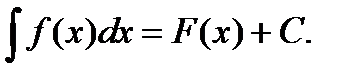 ;
; 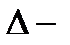 аралыєыныѕ ішкі нїктелерінде
аралыєыныѕ ішкі нїктелерінде 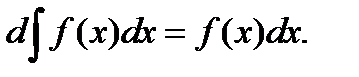 ;
; 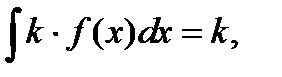
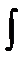 f(X)dx, k – тўраќты
f(X)dx, k – тўраќты
Егер 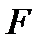 функциясы
функциясы 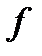 функциясының
функциясының  аралығындағы алғашқы функциясыболса,онда: 1)
аралығындағы алғашқы функциясыболса,онда: 1) 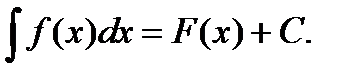 2)
2) 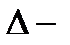 аралығының ішкі нүктелерінде
аралығының ішкі нүктелерінде 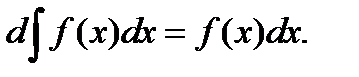 3)
3) 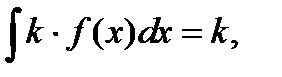
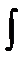 f(X)dx, k – тұрақты
f(X)dx, k – тұрақты
Екінші тамаша шектің формуласын көрсетіңіз С) 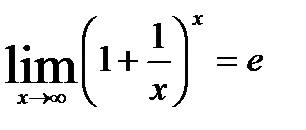
Интегралды табыңыз 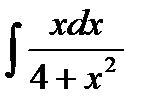 Е)
Е) 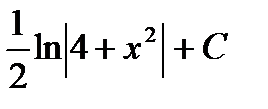
Кездейсоқ шама Х тығыздық үлестіру 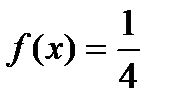 функциясы арқылы (-2;2) аралығында берілген, одан тыс
функциясы арқылы (-2;2) аралығында берілген, одан тыс 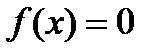 Х-тің дисперсиясы Д(х)-ті табыңыз: С)
Х-тің дисперсиясы Д(х)-ті табыңыз: С) 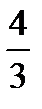
Келесі тұжырымдардың қайсысы ақиқат? Д) жүйенің үйлесімділігі бос мүшелерге тәуелді
Кері матрицаны табыңыз: 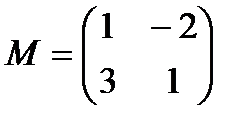 А)
А) 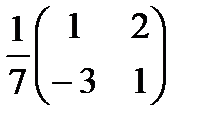
Комплекс санның аргументін тап: 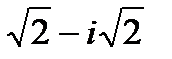 С)
С) 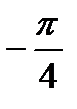
Коэффициенттері тұрақты біртекті сызықты дифференциалдық теңдеудің 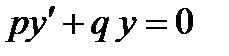
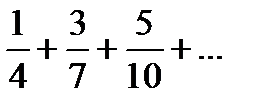 қатарының жалпы мүшесін жазыңыз: С)
қатарының жалпы мүшесін жазыңыз: С) 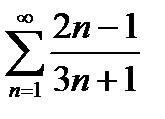
Лопиталь ережесін пайдаланып 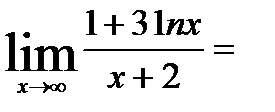 шекті табыңыздар:Е) 0
шекті табыңыздар:Е) 0
Лопиталь ережесін қолданып функцияның шегін табыңыз: Д) 12
Лопиталь ережесін қолданып функцияның шегін табыңыз 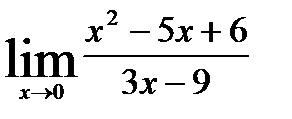 Е)
Е) 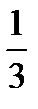
М(1,-1) нүктесінен өтетін және 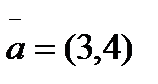 векторына перпендикуляр болатын түзудің теңдеуі: А)
векторына перпендикуляр болатын түзудің теңдеуі: А) 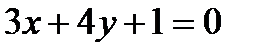
М(-3,5) нүктесінен өтетін және 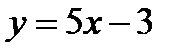 түзуіне параллель болатын түзудің теңдеуі
түзуіне параллель болатын түзудің теңдеуі 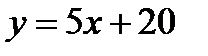
М(5;2) нүктесінен 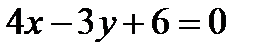 түзуіне дейінгі арақашықтықВ) 4
түзуіне дейінгі арақашықтықВ) 4
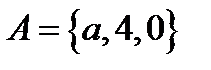 мен
мен 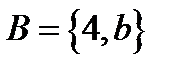 жиындарының бірігуін көрсететін өрнек: 1)
жиындарының бірігуін көрсететін өрнек: 1)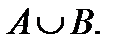 2)
2) 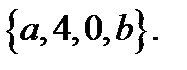 3)
3) 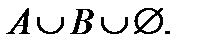
Мына функциялардың қайсысы 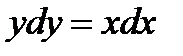 теңдеуінің шешуі болады:
теңдеуінің шешуі болады: 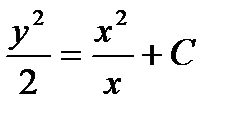 ;
; 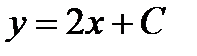
Мына шектер 3-ке тең болады: 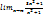 ;
; 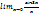 ;
; 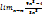
Нормальдық үлестіру түрін көрсетіңіз: Е) 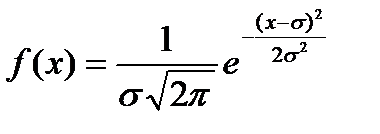
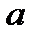 -ның қандай мәнінде
-ның қандай мәнінде 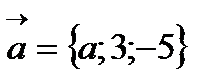 және
және 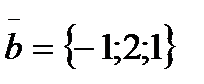 векторлары перпендикулярВ)1
векторлары перпендикулярВ)1
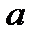 -ның қандай мәнінде
-ның қандай мәнінде 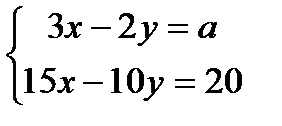 жүйе шексіз көп шешім қабылдайды?
жүйе шексіз көп шешім қабылдайды? 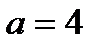
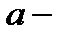 ның қандай мәнінде берілген жүйенің тек жалғыз шешімі болады?
ның қандай мәнінде берілген жүйенің тек жалғыз шешімі болады? 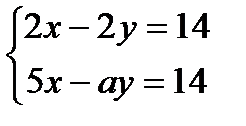 А)
А) 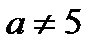
Нысанаға тигізудің салыстырмалы жиілігі 0,85 болды. 100 рет атқанда нысанаға тигізу санын табыңыз:Е) 85
Ойын сүйегі лақтырылды. Үштен артық ұпай түсу ықтималдығын табыңыз: В) 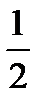
Ох өсімен және 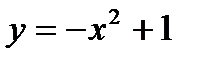 параболасымен шектелген фигураның ауданын есептеңіз:В)
параболасымен шектелген фигураның ауданын есептеңіз:В) 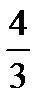 өзгерту тәсілі
өзгерту тәсілі
Студент 15 сұрақтың 6 біледі. Екі сұрақ қойғанда студенттің сынақ алу ықтималдығын табыңыз: Е) 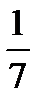
Теңдеулердің қайсысы айнымалдары ажыратылатын теңдеуге жатады? А) 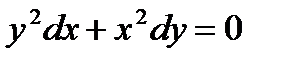
Тұрақты санның туындысыВ) Нөлге тең
Ұштары А(2; 3; 3) және В(-16; 21; -9) болатын кесіндіні 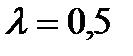 қатынасында бөлетін С нүктесінің координаттары:А) С(-4; 9; -1)
қатынасында бөлетін С нүктесінің координаттары:А) С(-4; 9; -1)
Үздікссіз кездейсоқ шама Х-тің тығыздық үлестіру берілген 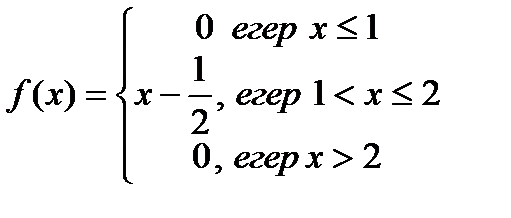
Үш белгісізі бар үш сызықты теңдеулер жүйесінің жалғыз шешімі болады, тек қана сонда , егер бұл жүйенің анықтауышы. А) нольге тең болмаса
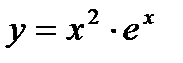 функцияның туындысын тең: А)
функцияның туындысын тең: А)