Линейные и квадратичные функции
 Линейная функция
Линейная функция 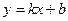 . Функция определена на всей числовой прямой,
. Функция определена на всей числовой прямой, 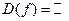 . Множество ее изменения – также множество всех действительных чисел,
. Множество ее изменения – также множество всех действительных чисел, 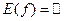 . Функция не ограничена. Она не имеет точек экстремума. При
. Функция не ограничена. Она не имеет точек экстремума. При 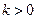 функция является возрастающей, при
функция является возрастающей, при 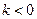 – убывающей. При
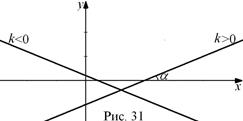
– убывающей. При 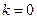 функция является постоянной. Графиком линейной функции является прямая. Угловой коэффициент k прямой равен тангенсу угла между прямой и положительным направлением оси абсцисс,
функция является постоянной. Графиком линейной функции является прямая. Угловой коэффициент k прямой равен тангенсу угла между прямой и положительным направлением оси абсцисс, 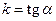 (рис. 31). Из аксиом геометрии известно, что если две точки прямой принадлежат плоскости, то и вся прямая принадлежит плоскости. Поэтому для построения графика линейной функции достаточно задать две точки.
(рис. 31). Из аксиом геометрии известно, что если две точки прямой принадлежат плоскости, то и вся прямая принадлежит плоскости. Поэтому для построения графика линейной функции достаточно задать две точки.
Квадратичная функция 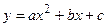 (
( 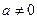 ). Функция определена на всей числовой прямой. Графиком квадратичной функции является парабола.
). Функция определена на всей числовой прямой. Графиком квадратичной функции является парабола.
Для построения графика квадратичной функции целесообразно преобразовать формулу, выделив полный квадрат: 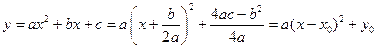 , где
, где 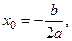
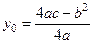 . Таким образом, получаем, что вершина параболы находится в точке с координатами
. Таким образом, получаем, что вершина параболы находится в точке с координатами 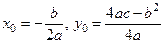 . График квадратичной функции симметричен относительно прямой
. График квадратичной функции симметричен относительно прямой 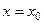 .
.
При 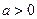 ветви параболы направлены вверх. В точке
ветви параболы направлены вверх. В точке 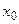 функция имеет минимум и принимает в этой точке наименьшее значение. При
функция имеет минимум и принимает в этой точке наименьшее значение. При 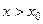 функция возрастает, при
функция возрастает, при 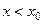 функция убывает. В этом случае квадратичная функция ограничена снизу и не ограничена сверху.
функция убывает. В этом случае квадратичная функция ограничена снизу и не ограничена сверху.
При 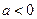 ветви параболы направлены вниз. В точке
ветви параболы направлены вниз. В точке 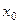 функция имеет максимум и принимает в этой точке наибольшее значение. При
функция имеет максимум и принимает в этой точке наибольшее значение. При 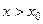 функция убывает, при
функция убывает, при 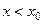 функция возрастает. В этом случае квадратичная функция ограничена сверху и не ограничена снизу.
функция возрастает. В этом случае квадратичная функция ограничена сверху и не ограничена снизу.
Если дискриминант соответствующего квадратного уравнения положителен, то парабола пересекает ось абсцисс в двух точках. Если дискриминант равен нулю, то парабола касается оси абсцисс. Если дискриминант отрицателен, то парабола расположена выше оси абсцисс, если 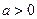 , и ниже оси абсцисс, если
, и ниже оси абсцисс, если 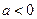 .
.
 Пример 10. Постройте графики функций
Пример 10. Постройте графики функций 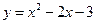 и
и 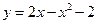 .
.
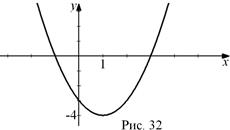
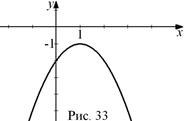 Решение. Вершина параболы
Решение. Вершина параболы 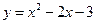 имеет координаты
имеет координаты 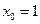 и
и 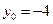 . Так как старший коэффициент
. Так как старший коэффициент 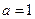 положителен, то ветви параболы направлены вверх. Также, решив уравнение
положителен, то ветви параболы направлены вверх. Также, решив уравнение 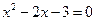 , можно найти точки пересечения с осью абсцисс:
, можно найти точки пересечения с осью абсцисс: 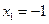 и
и 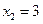 (рис. 32).
(рис. 32).
Для параболы 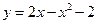 аналогично получаем, что
аналогично получаем, что 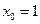 и
и 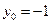 , и ветви ее направлены вниз. Данная парабола не имеет точек пересечения с осью абсцисс, так как дискриминант соответствующего квадратного уравнения отрицателен (рис. 33).
, и ветви ее направлены вниз. Данная парабола не имеет точек пересечения с осью абсцисс, так как дискриминант соответствующего квадратного уравнения отрицателен (рис. 33).
Построение графиков
Дробно-линейных функций
Функция вида 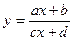 , где
, где 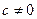 и
и 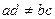 , называется дробно-линейной. Графиком этой функции является гипербола.
, называется дробно-линейной. Графиком этой функции является гипербола.
Частным случаем дробно-линейной функции является функция обратной пропорциональности 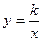 . График этой функции состоит из двух ветвей, симметричных относительно начала координат. При
. График этой функции состоит из двух ветвей, симметричных относительно начала координат. При 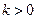 гипербола расположена в первой и третьей четвертях, при
гипербола расположена в первой и третьей четвертях, при 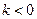 – во второй и четвертой четвертях.
– во второй и четвертой четвертях.
Пример 11. Постройте график функции 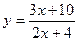 .
.
Решение. Выделим целую часть дроби 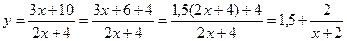 .
.
Таким образом, уравнение, которым задается график функции, примет вид 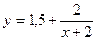 . График заданной функции получается из графика функции
. График заданной функции получается из графика функции 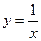 сдвигом на 2 единицы по оси OX влево, растяжением вдоль оси OY в 2 раза и сдвигом на 1,5 единицы по оси OY вверх.
сдвигом на 2 единицы по оси OX влево, растяжением вдоль оси OY в 2 раза и сдвигом на 1,5 единицы по оси OY вверх.
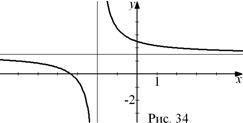 Заметим, что график функции не пересекает прямые
Заметим, что график функции не пересекает прямые 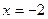 и
и 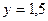 , хотя и приближается к ним достаточно близко. Такие прямые называются асимптотами графика функции. График дробно-линейной функции имеет две асимптоты – вертикальную
, хотя и приближается к ним достаточно близко. Такие прямые называются асимптотами графика функции. График дробно-линейной функции имеет две асимптоты – вертикальную 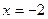 и горизонтальную
и горизонтальную 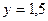 . Построение графика удобно начинать именно с нахождения асимптот: для нахождения вертикальной асимптоты приравниваем знаменатель дроби нулю, а для нахождения горизонтальной асимптоты выделяем целую часть дроби (рис. 34).
. Построение графика удобно начинать именно с нахождения асимптот: для нахождения вертикальной асимптоты приравниваем знаменатель дроби нулю, а для нахождения горизонтальной асимптоты выделяем целую часть дроби (рис. 34).
Построение графика произвольной дробно-линейной функции 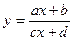 выполняется по алгоритмам, разобранным в примере 11.
выполняется по алгоритмам, разобранным в примере 11.
Упражнения
8. Постройте графики функций:
а) 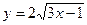 ; б)
; б) 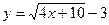 ;
;
в) 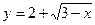 ; г)
; г) 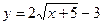 ;
;
д) 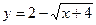 ; е)
; е) 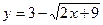 .
.
9. Постройте графики функций:
а) 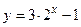 ; б)
; б) 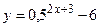 ;
;
в) 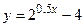 ; г)
; г) 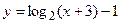 ;
;
д) 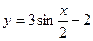 ; е)
; е) 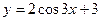 ;
;
ж) 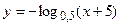 ; з)
; з) 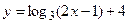 .
.
10. Постройте графики функций:
а) 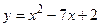 ; б)
; б) 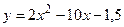 ;
;
в) 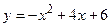 ; г)
; г) 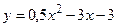 ;
;
д) 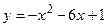 ; е)
; е) 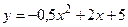 .
.
11. Постройте графики функций:
а) 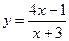 ; б)
; б) 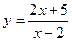 ; в)
; в) 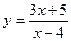 ;
;
г) 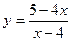 ; д)
; д) 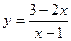 ; е)
; е) 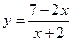 .
.
