Линейный закон фильтрации (закон Дарси)

Экспериментальный закон, полученный А.Дарси, имел вид:

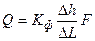, (1.7)

где Q - объемный расход жидкости; F - площадь поперечного сечения трубы, заполненной песком; Dh = h₁-h₂ - потери напора на длине DL; K_ф - коэффициент фильтрации, зависящий как от структуры пористой среды, так и от свойств фильтрующейся жидкости.

Поскольку Dh=DР/rg, а V=Q/F, то уравнение (1.7) можно представить в виде:

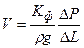. (1.8)

Сопоставим формулы опытного и теоретического законов фильтрации - выражения (1.5) и (1.8). Видно, что

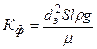, откуда .

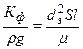К_ф обычно используется в гидротехнических расчетах, где приходится иметь дело с одной жидкостью - водой. При решении задач фильтрации различных жидкостей приходится пользоваться различными значениями К_ф. Кроме того, коэффициент фильтрации по-разному рассчитывается в зависимости от способа определения Sl. Это неудобно, поэтому при исследовании фильтрации нефти и газа пользуются коэффициентом проницаемости, который позволяет разделить влияние пористой среды и жидкости.

Проницаемость - это свойство пористой среды пропускать через себя жидкости и газы при наличии перепада давления.

Обозначим К=d_э²Sl.

Тогда формулы (1.5) и (1.6) запишутся в виде:

Скорость фильтрации прямо пропорциональна градиенту давления (закон Дарси).

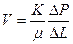; (1.9)

.

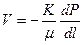Коэффициент проницаемости зависит только от свойств пористой среды и не зависит от свойств жидкости.

К/m - коэффициент подвижности.

Единицы измерения проницаемости: СИ - м²; мкм²;

СГС - Д (Дарси), мД.

1 Д =1,02×10^-12 м² » 1 мкм².

200 мД = 0,200 мкм².

Физический смысл размерности (площадь) заключается в том, что проницаемость как бы характеризует величину площади сечения каналов пористой среды, по которым в основном происходит фильтрация.

Пористость и проницаемость характеризуют фильтрационно-емкостные свойства пласта (ФЕС), причем пористость характеризует емкость, а проницаемость - пропускную способность.

Приведенное давление

Формулы (1.9) справедливы для фильтрации жидкости в горизонтальном направлении. В тех случаях, когда скорость фильтрации направлена не по горизонтали, наряду с разностью давлений DР на фильтрацию оказывает влияние сила тяжести.

Рассмотрим элемент наклонного пласта.

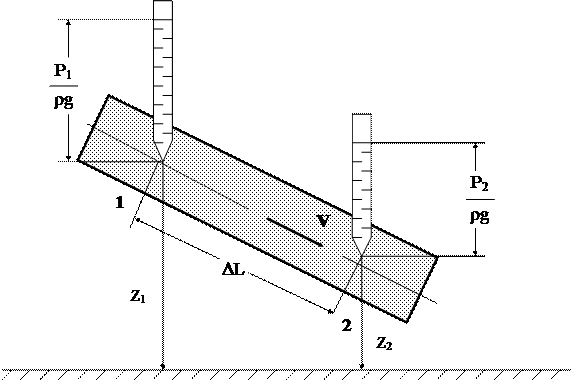Величины напоров в сечениях 1 и 2 составляют:

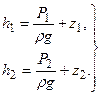, (1.10)

где z₁ и z₂ - расстояния сечений 1 и 2 от некоторой условной горизонтальной плоскости отсчета.

Потеря напора при фильтрации жидкости в рассматриваемом наклонном пласте:

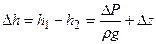, где Dz=z₁-z₂ .

Соответственно потеря давления:

.

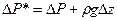Тогда закон Дарси запишется в виде:

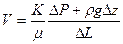или .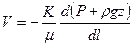

Величину P*=P+rgz называют приведенным давлением.

Тогда в общем случае линейный закон фильтрации можно записать так:

.

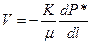Приведенным пластовым давлением, пересчитанным на какую-либо условную поверхность (чаще всего ВНК или ГНК), пользуются для характеристики залежей.

P_пл.пр. = Р_пл.а ± rgZ ,

где Р_пл.а - абсолютное пластовое давление; Z - расстояние от середины пласта в точке вскрытия скважиной до плоскости приведения.

Если плоскость приведения находится ниже середины пласта, то приведение осуществляется со знаком плюс, если выше - минус.

Р_{1 пл.пр.} = Р_1а + r_нgZ₁ ;

Р_{2 пл.пр.} = Р_2а - r_вgZ₂ .

Если устье скважины находится выше пьезометрической поверхности, то абсолютное давление находим по формуле:

Р_а = (H - h)r_жg ,

где H - глубина скважины от устья до середины пласта; h - глубина пьезометрического уровня от устья.

В скважинах с устьями ниже пьезометрической поверхности

Р_а = H r_жg + Р_у ,

где Р_у - давление на устье скважины.