Графический метод решения ЗЛП с двумя переменными

Графический метод основан на геометрической интерпретации ЗЛП и применяется в основном для решения задач в двумерном пространстве, т.е. когда n=2, и только некоторых задач трехмерного пространства, т.к. довольно трудно построить многогранник решений, который образуется в результате пересечения полупространств. Задачу пространства размерности больше трех изобразить графически вообще невозможно. Данный метод основывается на возможности графического изображения области допустимых решений задачи и нахождения среди них оптимального решения.

Формулировка: найти максимальное значение функции Z=C₁x₁+C₂x₂ (1)

при ограничениях

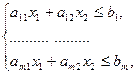(2)

x₁ ³ 0, x₂ ³ 0. (3)

Допустим, что система (2) при условии (3) совместна, т.е. имеет хотя бы одно решение, и ее многоугольник решений ограничен. Каждое из неравенств (2) и (3), как отмечалось выше, определяет полуплоскость с граничной прямой: a_i1x₁+a_i2x₂=b_i (i=1,2,...,m), x₁=0, x₂=0. Область допустимых решений задачи строится как пересечение (общая часть) областей решений каждого из заданных ограничений.

Для нахождения среди допустимых решений оптимального решения используют линии уровня и опорные прямые.

Линией уровня называется прямая, на которой целевая функция задачи принимает постоянное значение, т.е. имеет вид C₁x₁+C₂x₂ = const. Все линии уровня параллельны между собой. Их нормаль - вектор N=(C₁,C₂).

Опорной прямой называется линия уровня, которая имеет хотя бы одну общую точку с ОДР и по отношению к которой эта область находится в одной из полуплоскостей.

Тогда поставленной ЗЛП можно дать следующую интерпретацию: найти точку многоугольника решений, в которой прямая C₁x₁+C₂x₂ = const является опорной и функция Z при этом достигает максимума.

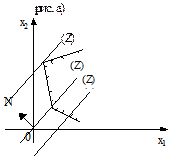
Построим многоугольник системы ограничений (2) и график линейной функции при Z=0 (см. рис.). Значения Z=C₁x₁+C₂x₂ возрастают в направлении вектора N=(C₁,C₂), поэтому нужно прямую C₁x₁+C₂x₂=0 передвигать параллельно самой себе в направлении вектора N.

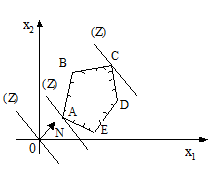Из рис. следует, что прямая дважды становится опорной по отношению к многоугольнику решений (в точках A и C), причем минимальное значение Z принимает в точке A, а максимальное - в точке C. Координаты точки C(x₁,x₂) находим, решая систему уравнений прямых BC и CD.

Если многоугольник решений представляет собой неограниченную многоугольную область, возможны два случая.

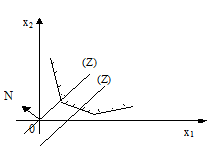
Случай 1. Прямая C₁x₁+C₂x₂ = const, передвигаясь в направлении вектора N или противоположно ему, постоянно пересекает многоугольник решений и ни в какой точке не является опорной к нему. В этом случае линейная функция не ограничена на многоугольнике решений как сверху, так и снизу.

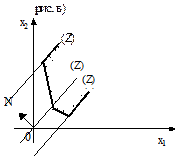
Случай 2. Прямая, передвигаясь, все же становится опорной относительно многоугольника решений. Тогда в зависимости от вида области линейная функция может быть ограниченной сверху и неограниченной снизу (a), ограниченной снизу и неограниченной сверху (б), либо ограниченной как снизу так и сверху (в).

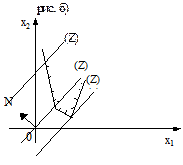Алгоритм графического метода решения ЗЛП с двумя переменными.

1. Построить ОДР.

2. Если ОДР – пустое множество, то задача не имеет решений ввиду несовместности системы ограничений.

3. Если ОДР является непустым множеством, построить нормаль линий уровня N=(C₁,C₂) и одну из линий уровня, имеющую общие точки с этой областью.

4. Линию уровня переместить до опорной прямой в задаче на максимум в направлении нормали, в задаче на минимум – в противоположном направлении.

5. Если при перемещении линии уровня по ОДР в направлении, соответствующем приближению к экстремуму целевой функции, линия уровня уходит в бесконечность, то задача не имеет решения ввиду неограниченности целевой функции.

6. Если ЗЛП имеет оптимальное решение, то для его нахождения решить совместно уравнения прямых, ограничивающих ОДР и имеющих общие точки с соответствующей опорной прямой. Если целевая функция достигает экстремума в двух угловых точках, то задача имеет бесконечное множество решений. Оптимальным решением является любая выпуклая линейная комбинация этих точек.

7. После нахождения оптимальных решений вычислить значение целевой функции на этих решениях.

Примеры задач, решаемых графическим методом.

а) Задача о составлении плана выпуска продукции. Найти максимальное значение функции Z = 2x₁ + 3x₂ при ограничениях 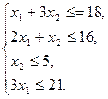, x₁ ³ 0, x₂ ³ 0.

Решение. Построим многоугольник решений (см. рис ). Для этого в системе координат x₁0x₂ на плоскости изобразим граничные прямые

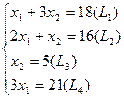, x₁ = 0, x₂ = 0.

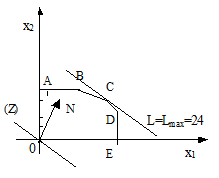
Многоугольником решений задачи является ограниченный шестиугольник OABCDE.

Для построения прямой 2x₁ + 3x₂ = 0 строим радиус-вектор N=(2; 3) и через точку O проводим прямую, перпендикулярную ему. Построенную прямую Z = 0 перемещаем параллельно самой себе в направлении вектора N. Из рис. следует, что опорной по отношению к многоугольнику решений эта прямая становится в точке C, где функция Z принимает максимальное значение. Точка C лежит на пересечении прямых ВС и CD. Для определения ее координат решим систему уравнений

.

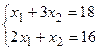Оптимальный план задачи: x₁=6; x₂=4. Подставляя значения x₁ и x₂ в линейную функцию, получаем L_max = 2×6+3×4=24.

Таким образом, для того, чтобы получить максимальную прибыль в размере 24 гривен, необходимо запланировать производство 6 ед. продукции P₁ и 4 ед. продукции P₂.

b) Задача составления рациона. Найти минимальное значение функции
L = 4x₁ + 6x₂ при ограничениях 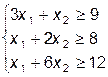x₁³0, x₂³0.

Решение. Построим многоугольник решений (рис.). Для этого в системе координат x₁0x₂

на плоскости изобразим граничные прямые

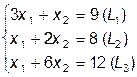, x₁ = 0, x₂ = 0.

Установим, какую полуплоскость определяет каждое неравенство относительно граничной прямой. В результате получим неограниченную многоугольную область с угловыми точками A, B, C,D.

Построим вектор, N=(4; 6) и прямую 4x₁ + 6x₂ = 0 (L). Перемещаем прямую L параллельно самой себе в направлении вектора N. Из рис. следует, что она впервые коснется многогранника решений и станет опорной по отношению к нему в угловой точке B; если прямую перемещать далее в направлении вектора N, то значения линейной функции на многограннике решений возрастут, значит, в точке B линейная функция принимает максимальное значение. Точка B лежит на пересечении прямых L₁ и L₂ ; для определения ее координат решим систему уравнений .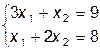

Имеем: x₁=2; x₂=3. Подставляя найденные значения в линейную функцию, получаем L_min = 4×2+6×3=26.

Для того, чтобы обеспечить минимум затрат (26 коп. в день), необходимо дневной рацион составить из 2 кг корма I и 3 кг корма II.