Построение графиков функций

При построении графиков функций с помощью производных полезно придерживаться такого плана:

1. Находят область определения функции и определяют точки разрыва, если они имеются.

2. Выясняют, не является ли функция четной или нечетной; проверяют её на периодичность.

3. Определяют точки пересечения графика функции с координатными осями, если это возможно.

4. Находят критические точки функции.

5. Определяют промежутки монотонности и экстремумы функции.

6. Определяют промежутки вогнутости и выпуклости кривой и находят точки перегиба.

7. Находят асимптоты графика функции.

8. Используя результаты исследования, соединяют полученные точки плавной кривой. Иногда для большей точности графика находят несколько дополнительных точек; их координаты вычисляют, пользуясь уравнением кривой.

Задание 38.Исследовать функцию и построить график: .

Решение: 1. Функция определена на интервале (-¥; ¥). Точек разрыва нет.

2. Имеем . Функция не является ни четной, ни нечетной, так как и .

3. Найдем точки пересечения графика функции с осями координат. Если у = 0, то , откуда , т.е. . Значит, кривая пересекает ось абсцисс в точках (-3; 0) и (1; 0). Если х = 0, то из равенства следует у = -3, т.е. кривая пересекает ось ординат в точке (0; -3).

4. Найдем критические точки функции. Имеем .

5. Область определения функции разделится на промежутки (-¥; -1) и (-1; ¥). Знаки производной 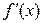в каждом промежутке можно найти непосредственной подстановкой точки из рассматриваемого промежутка. Так, . Следовательно, в промежутке (-¥; -1) функция убывает, а в промежутке (-1; ¥) – возрастает. При функция имеет минимум, равный , М(-1; 4).

Составим таблицу:

х	(-¥; -1)	-1	(-1; ¥)
	-		+

6. Находим , т.е. . Следовательно, кривая вогнута на всей области определения и не имеет точек перегиба.

7. Вертикальная асимптота имеет вид , если и (или ). Так как функция определена на интервале , то точек разрыва нет, нет и вертикальных асимптот.

Прямая называется горизонтальной асимптотой графика функци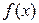и при , если .

В нашем случае , следовательно, горизонтальных асимптот нет.

Прямая называется наклонной асимптотой графика функции 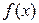, если существуют пределы:

и

В нашем случае:

- не существует.

- не существует.

Следовательно, наклонных асимптот данная функция не имеет.

8. Построим все найденные точки в прямоугольной системе координат и соединим их плавной линией (рис. 5).

у

А(-3;0) -1 В(1;0)

0 х

-3

М -4

Рис. 5

Ответы

1а)

1б)

2а)

2б)

3а)

Можно упростить выражение до нахождения производной, сократив на х, тогда

3б)

4а) .

4б) .

5а) .

5б) , если решать по формуле IV – (производной произведения).

, если решать по формуле VI (производной частного).

После преобразования получим:

.

6а) .

6б) .

7а) .

7б) .

8а) .

8б) .

9а) .

9б) .

10а) .

10б) .

11а) .

11б) .

12а) .

12б)

13а) .

13б) .

14а) .

14б)

15а) .

15б)

16а)

. По формулам 14, 18.

16б)

. По формулам 11, 18, V, 10, 17.

17а)

.

17б)

.

18а)

.

18б) .

19а) Линия 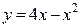ось 0х пересекает в точках, где у = 0. Найдем координаты этих точек .

Это точки А(0; 0) и В(4; 0).

Производная 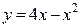будет равна .

Для точки А(0; 0) уравнение касательной:

Для точки А(0; 0) уравнение нормали:

Для точки В(4;0)

уравнение касательной

Уравнение нормали для точки В(4;0)