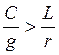Синусоидальный режим в однородной линии. Обратная волна. Длина волны. Фазовая скорость

Фазовая скорость обратной волны 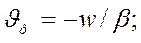знак «-» указывает, что обратная волна движется в направлении, противоположном направлению прямой волны.

Итак, мгновенное напряжение можно рассматривать как сумму двух волн, движущихся в противоположных направлениях, причём каждая из этих волн затухает в направлении движения.

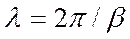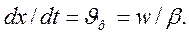На основании формул и запишем:

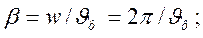
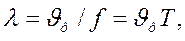
т.е. за время, равное одному периоду, падающая и отражённая волны перемещаются на расстояние, равное длине волны.

54. Математическая модель длинной линии при синусоидальном воздействии. Коэффициенты отражения n₁ и n₂.

Линии, длина которых соизмерима с длиной волны, считаются длинными линиями. На высоких частотах практически любая протяжённая электрическая цепь становится «длинной» по отношению к длине волны.

Возвращаясь к уравнениям 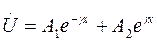и 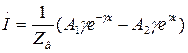и записывая прямую и обратнуюволны в комплексной форме, имеем: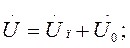

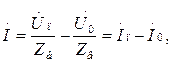
где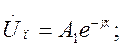

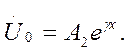
Напряжение и ток прямой и обратный волн связаны законом Ома: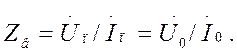

Это соотношение объясняет смысл термина «волновое сопротивление».

Постоянные интегрирования A1 и A2, находятся в зависимости от напряжения и тока в начале линии при заданных граничных условиях. При x=0

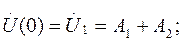
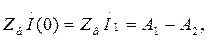
откуда

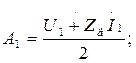
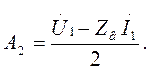
Введём понятие коэффициента отражения волны в начале линии

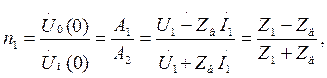
где 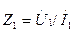- входное сопротивление линии.

Подстановка A1 и A2 даёт:

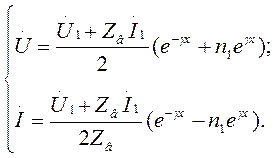
Если заданы граничные условия на конце линии, то удобнее отсчитывать расстояние от конца, приняв координату 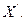Для A1 и A2 получаем следующие выражения:

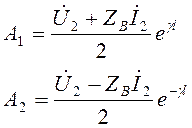
Получим окончательные результаты для U и I

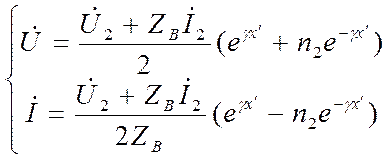
Где аналогично предыдущему n2-коэфициент отражения в конце линии

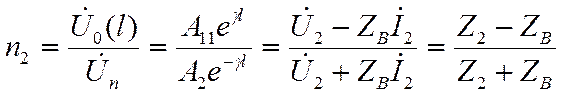
Где 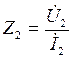выходное сопротивление в конце линии.

55. Вторичные параметры однородной линии. Зависимость коэффициентов a и b от частоты. Волновое сопротивление линии.

Вторичными линиями, или характеристическими, параметрами линии являются коэффициент ослабления, коэффициент фазы 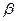и волновое сопротивление 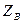, которые выражаются через первичные параметры линии и частоту.

Из выражения 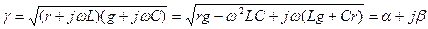следует, что 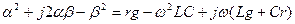, откуда ; .

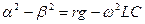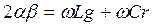Совместное решение этих уравнений дает

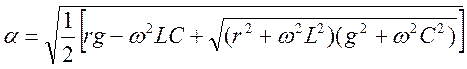
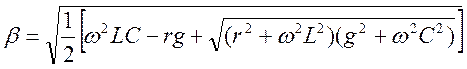
Из полученных выражений следует, что 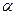и 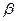в общем случае зависят от частоты. Однако, как показывает исследование, в отличие от коэффициента ослабления, который изменяется в сравнительно ограниченных пределах, коэффициент фазы неограниченно растет с частотой.

Полученные выражения неудобны для практического применения ввиду их громоздкости. Существует ряд приближенных расчетных формул для вычисления вторичных параметров линии, учытывающих, что в области высоких частот сопротивление 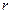весьма мало по сравнению с 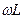, а проводимость 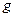ничтожна мала по сравнению с .

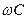Для уменьшения потерь при передаче электромагнитной энергии по линии стремятся к тому, чтобы сопротивление линии и проводимость изоляции были по возможности малы.

Волновое сопротивление линии

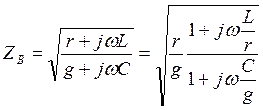
При постоянном токе 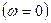и бесконечной частоте 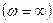имеет действительные значения

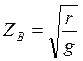и 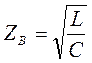В остальной части диапазона частот волновое сопротивление имеет емкостный характер, так как обычно